(QUI il quiz)

Un plauso, come è ormai abitudine, al nostro carissimo Andy, che non sbaglia un colpo e tiene vivi, praticamente da solo, i quiz "estivi".

Questo articolo descrive e risolve il problema di Regiomontano, che altro non è che la soluzione del quiz sul quadro appeso alla parete. In realtà, Regiomontano è il soprannome dato al matematico tedesco tedesco Johannes Müller (1436 -1476). Il problema ammette varie soluzioni, ma noi presentiamo quella basata sulla geometria elementare.

Le condizioni migliori per ammirare un quadro (AB) posto in alto su una parete sono sicuramente quelle che permettono all’occhio di guardare il quadro con l’angolo ϑ maggiore. Ciò vuol dire non stare né troppo vicino né troppo lontano dalla parete, come mostra la Fig. 1.

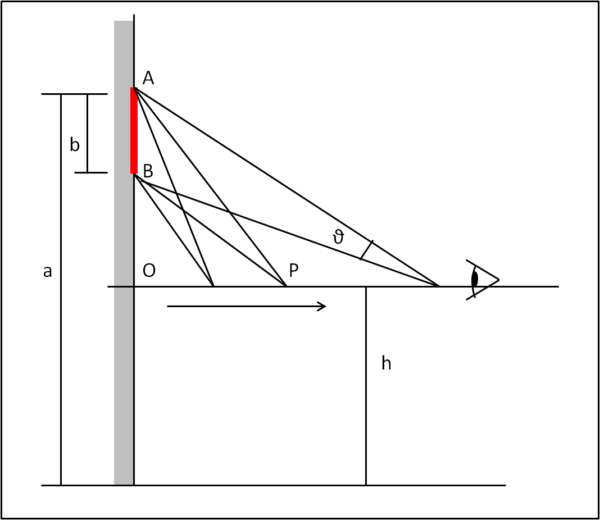
L’ammiratore e, quindi, i suoi occhi devono spostarsi lungo la perpendicolare alla parete, mantenendo , ovviamente, costante l’altezza h dal pavimento. Tutto ciò per rendere massimo l’angolo ϑ. Esiste una e una sola posizione di P (occhio) per cui ciò avvenga. Quale sarà la distanza tra parete e occhio corrispondente?

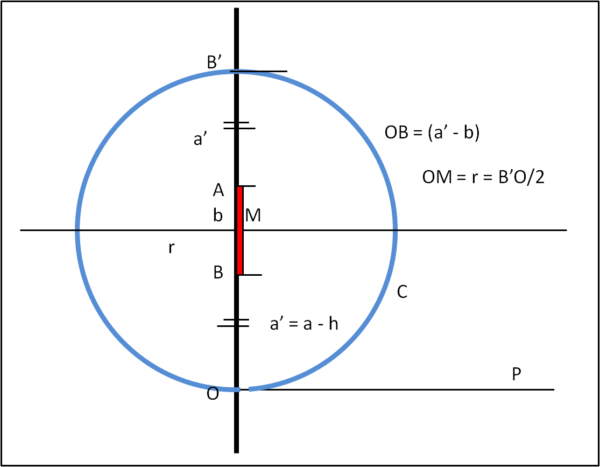
Per semplicità consideriamo come asse orizzontale quello passante per l’occhio (OP). Chiamiamo a - h = a', da cui:

BO = a  - b - h = a' - b

Sulla verticale passante per O riportiamo, a partire da A, il segmento BO, individuando B’

Il punto di mezzo di OB’ è , ovviamente, anche il punto di mezzo M del quadro. Tracciamo un cerchio di centro M e raggio pari a OB’/2, come mostra la Fig. 2

Facciamo scorrere la circonferenza  in senso orizzontale in modo da portare il centro in M’ in modo che essa intersechi la parete nei punti A e B del quadro (Fig. 3).

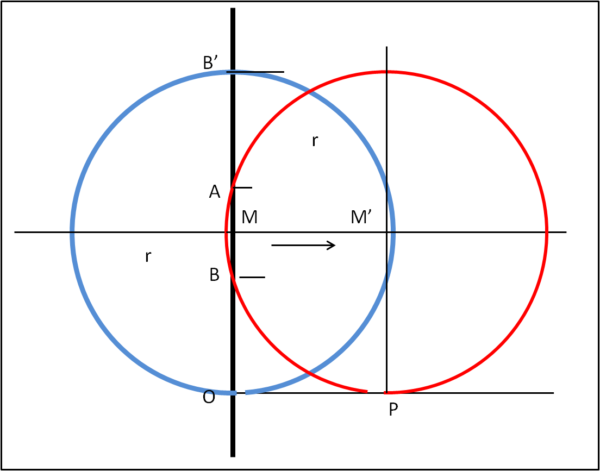
Congiungiamo A e B con il corrispondente punto di tangenza P e otteniamo il triangolo ABP in cui l’angolo in P è l’angolo alla circonferenza sotteso da AB (Fig. 4).

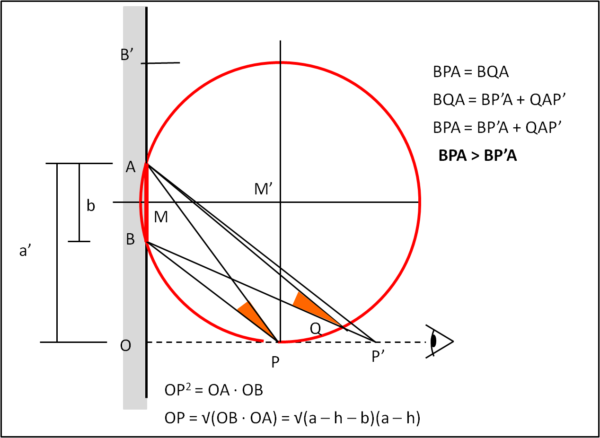
Qualsiasi altro punto P’ si prenda sull’asse OP si viene a costruire un triangolo come ABP’. L’angolo in P’ è sempre minore di quello in P. Infatti, considerando il triangolo ABQ troviamo che l’angolo in Q è uguale all’angolo in P (angoli alla circonferenza sottesi da uno stesso arco). Ma l’angolo in Q è uguale alla somma dell’angolo QAP’ e B’PA.

Sintetizzando, possiamo scrivere:

BPA = BQA

BQA = BP’A + QAP’

BQA > BP’A

Per calcolare la distanza OP basta ricordare il teorema della tangente-secante che abbiamo descritto nell’articolo sulla potenza di un punto.

Si ha che:

OP² = OA · OB

Dove OB = a' – b e OA = a'

si ottiene:

OP = √(a’ – b)a’