Non è la prima volta che parliamo di triangoli sferici. Tuttavia, in questo articolo vogliamo determinarne l'area, in un modo estremamente semplice, lavorando solo sulla superficie della sfera.

Sbucciamo un'arancia

Non è certo difficile tagliare un'arancia a spicchi, dato che uno spicchio sferico non è altro che la parte di sfera racchiusa tra due cerchi massimi, come mostra la Fig. 1

Noi, però, non vogliamo incidere in profondità il frutto, ma solo "sbucciarlo", ossia eliminare la buccia dello spicchio. Un po' come mostra la Fig. 2.

Bene, la buccia di uno spicchio prende il nome di fuso o -io preferisco- lunula sferica.

Cominciamo proprio con essa e vediamola rappresentata in Fig. 3, sotto varie angolazioni.

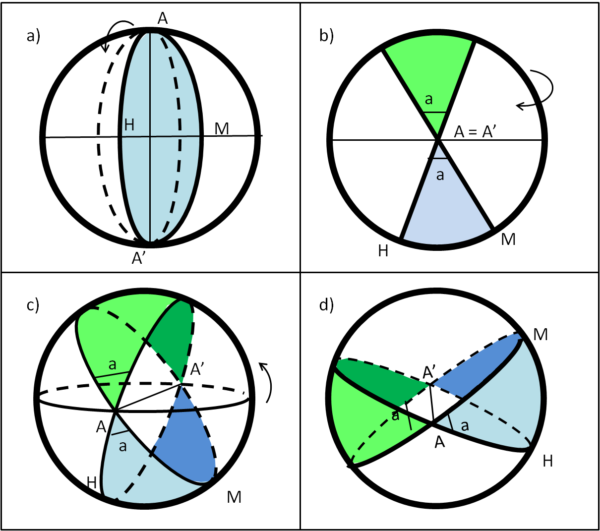
In realtà il procedimento che adottiamo determina sempre due lunule uguali (verde e azzurra). Non solo, però... i due cerchi massimi dividono la superficie dell'arancia in 4 lunule, uguali a due a due. Per adesso consideriamo la lunula di ampiezza minore (azzurra) e la sua "gemella" (verde).

Possiamo utilizzare la Fig. 3b dove si individua molto bene l'angolo diedro a compreso tra i due cerchi massimi. Esso è anche l'angolo che caratterizza la lunula sferica azzurra. e quella identica di colore verde.

E' immediato scrivere una semplice proporzione:

4π r²/2π = L(a)/a

dove 4π r² è l'area dell'intera superficie sferica e L(a) è l'area della lunula azzurra (o verde).

L(a) = 2 a r²               .... (1)

Formiamo un triangolo

Non ci vuole molto a ottenere un triangolo sferico. Basta tagliare la nostra lunula con un nuovo cerchio massimo, come mostra la Fig. 4.

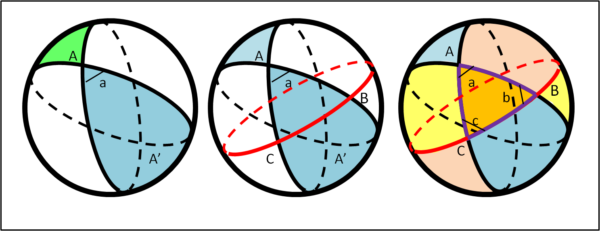
Il nuovo cerchio massimo introduce due nuove lunule (con le loro gemelle, che abbiamo colorato dello stesso colore). Le abbiamo colorate di rosa e di giallo. La loro intersezione è il triangolo sferico colorato in arancione con i suoi tre angoli a, b e c (ogni angolo identifica la coppia di lunule corrispondenti).

Notiamo che, per la completa simmetria della situazione, dalla parte opposta della sfera si viene a costruire un triangolo sferico perfettamente uguale ad ABC. Esso è formato, ovviamente dall'intersezione delle tre lunule "gemelle". Chiamiamo T la sua area.

Non ci resta che ragionare un pochino e non farsi confondere dalla visione tridimensionale della sfera.

Se sommiamo le aree delle tre lunule e quelle delle tre gemelle copriamo completamente la superficie sferica. Anzi, abbondiamo... Infatti, sommando le sei lunule siamo costretti ad aggiungere tre volte il triangolo sferico e il suo "gemello", mentre a noi basta contarli una volta...

Possiamo comunque scrivere che la somma delle sei lunule è uguale alla superficie sferica più 4 triangoli sferici (ne crescono solo 4, dato che due ci servono per completare la superficie sferica). In termini matematici semplicissimi:

2(L(a) + L(b) + L(c)) = 4πr² + 4T

4T = 2(L(a) + L(b) + L(c)) - 4πr²

T = (2(L(a) + L(b) + L(c)) - 4πr²)/4

T = (L(a) + L(b) + L(c))/ 2 - πr²

Ricordando la (1):

T = (2 a r² + 2 b r²  + 2 c r² )/ 2 - πr²

T = a r² +  b r²  +  c r² - πr²

T = r²(a + b + c - π)

Questa formula ci ricorda anche che la somma degli angoli di un triangolo sferico non è uguale a 180°, ma dipende dall'area del triangolo