Categorie: Matematica
Tags: circocentro Olimpiadi quadrati costruiti sui lati quiz triangolo
Scritto da: Vincenzo Zappalà
Commenti:15
Un quiz pre-olimpico ****
Torniamo a un quiz dedicato ai più bravi. Siamo sempre di fronte a un semplice triangolo, ma estremamente "subdolo". Non per niente questo problema di PURA GEOMETRIA è stato presentato a una competizione delle Olimpiadi di matematica.
La soluzione che riporto io potrebbe anche non essere la migliore e, quindi .... forza miei prodi!
La Fig. 1 illustra il problema.
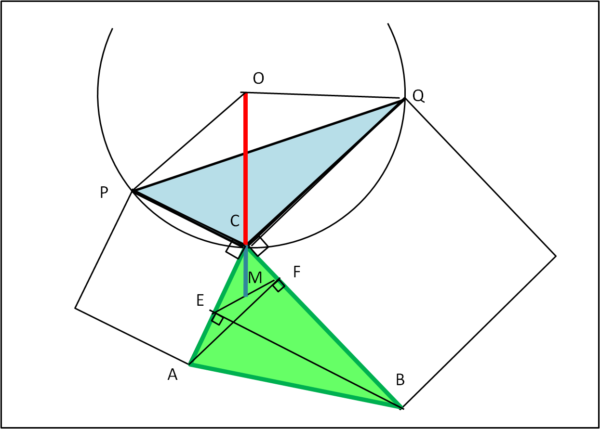
Abbiamo un triangolo qualsiasi ABC. Da A e da B tracciamo le perpendicolari ai lati opposti che individuano i punti F ed E. Il punto di mezzo del segmento EF lo chiamiamo M. Sui lati AC e BC del triangolo costruiamo due quadrati e siano P e Q i due vertici adiacenti al vertice C. Determiniamo in tal modo il triangolo QCP e il centro O del suo cerchio circoscritto.
Dimostrare che la retta congiungente O con C passa per M






15 commenti
Ahi, ahi... vedo che anche i più bravi (Pautasso compreso) stanno faticando... E pensare che la geometria da utilizzare è veramente elementare... Attendo con fiducia
Veramente Pautasso non aveva neppure visto questo nuovo quiz, essendo alle prese con una nuova planata del pavone che presto atterrerà nel Teatro.
Comunque ora gli dico di leggersi il quiz, giusto per vedere se lo capisce.
Aggiungo qualche linea al disegno originale, in questo modo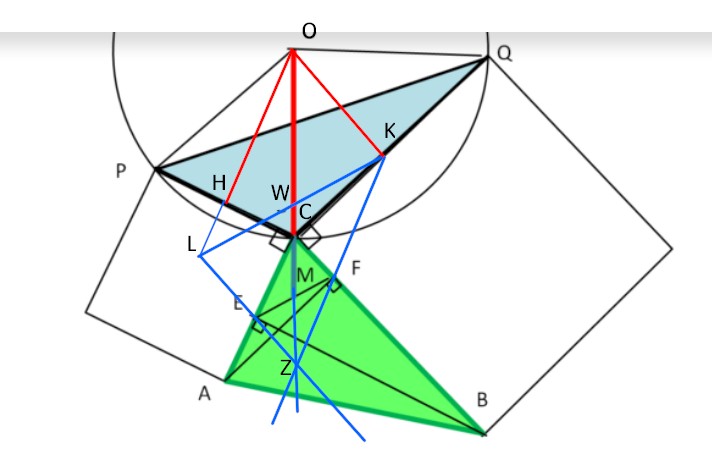
Traccio in rosso le altezze dei triangoli isosceli OCP e OCQ e ottengo i segmenti OH e OK
Da K traccio in blu la retta che passa Per F (parallela al lato AC (verde) e anche ad OH
sempre da K traccio in blu la parallela ad EF e la faccio intersecare con il prolungamento di OH nel punto L
Da L traccio in blu la parallela al lato CB (verde) e anche ad OK, fino a farla intersecare con il prolungamento di KF nel punto Z
A questo punto osservo il parallelogramma OLZK e traccio le sue diagonali OZ e LK che si intersecano in W
Le due diagonali si dividono reciprocamente a metà quindi LW = WK
Osservo che il triangolo LKZ è simile al triangolo EFZ quindi anche il segmento EF verrà diviso a metà dalla diagonale del parallelogramma e sarà EM = MF (come assunto nelle ipotesi del problema)
Lungo la diagonale OZ saranno quindi allineati i punti O W C M. e Z
Può anche essere la strada giusta... ma certe conclusioni vanno dimostrate per bene. Chi legge ha bisogno di capire ogni passaggio. Non tutti sono esperti ed è a loro che dobbiamo far amare la geometria. A partire da KF //AC e via dicendo. L'idea del parallelogramma è buona, ma bisogna spiegare meglio la sua costruzione. Fai ancora un piccolo sforzo!
Semplifico in questo modo
Traccio gli assi di CP e CQ. Passano ambedue per O e sono paralleli ai lati CA e CB
Traccio per il punto E la parallela a CB e per il punto F la parallela a CA Si intersecano nel punto Z
Ottengo così il parallelogramma OGZH dove i punti G e H sono le intersezioni degli assi con le parallele ai lati appena disegnate.
Internamente a questo parallelogramma c'è il parallelogramma più piccolo CEZF . In esso la diagonale CZ divide in due la diagonale EF proprio nel punto M.
Il segmento CZ (diagonale del parallelogramma piccolo) è contenuto in OZ, (diagonale del parallelogramma grande) pertanto i punti O C M Z sono allineati
Ho un dubbio... Chi mi dice che C stia sulla diagonale OZ ?
Rasserenati perché
Il punto C appartiene all'insieme dei punti di CZ. E CZ è un sottoinsieme di OZ
Quindi C appartiene a OZ
Aggiungo...
tu dici: "traccio per il punto E la parallela a CB ". Chi mi dice che passi per H ?
O, alternativamente, se traccio da H la parallela ad AC, chi mi dice che passi per F ?
Temo che figura faccia pensare ovvie cose che tali non sono... Magari mi sbaglio, convincimi
Dimmi se sei d'accordo sulla appertenenza di C alla diagonale OZ.
I punti G e H sono semplicemente le intersezioni degli assi con le parallele ai lati. Non sono punti pre determinati
Perché C deve appartenere alla diagonale? E perché HZ (parallela ad AC) deve passare per F ? Per trovare Z devi aver scelto G., Perché H sta su QC e invece G è fuori? Chi mi dice che FH è parallela
Tu tracci da H la parallela a OG, ma perché mai deve passare per F ?
Questa è la figura di partenza, contenuta nel testo.
Il punto O è il vertice dei due triangoli isosceli OCP e OCQ
Impongo il passaggio per il punto E di una retta parallela al lato CB
Impongo il passaggio per il punto F di una retta parallela al lato CA
Ecco la figura con queste aggiunte:
L'incrocio delle due retta blu a cui ho imposto il passaggio per E e per F lo chiamo Z.
Ho costruito in questo modo un parallelogramma CEZF in cui la diagonale EF e la diagonale CZ si intersecano nel punto M che è medio per il segmento CZ e anche par il segmento EF.
Tutti i punti da C a Z apparten gono alla diagonale CZ.
Ecco la figura completata con la lettera Z e la diagonale CZ
Su questa figura prolungo il segmento ZC verso l'alto. NON SO se incontrerò il punto O.
Facciamo ora l'ipotesi che O si trovi sul prolungamento di ZC.
Traccio da O una retta parallela a CA e interseco la retta ZE in G:
Traccio da O una retta parallela a CB e interseco la retta ZF in in H.
Ricordo che per costruzione il punto O è il vertice dei due triangoli isosceli OCP e OCQ
Ecco il disegno di queste aggiunte:
Sotto questa ipotesi vedo il parallelogramma OGZH in cui è contenuto il parallelogramma più piccolo CEZF la cui diagonale CZ è sovrapposta alla diagonale grande OZ.
Posso affermare quindi che la retta congiungente O con C passa per M
Ma cosa succederebbe se il punto O non si trovasse sul percorso della retta passante per ZC ?
Spostando lateralmente il punto O i due triangoli OPC e OCQ non sarebbero più isosceli e O non sarebbe centro del cerchio.
Quindi negando l'ipotesi otteniamo un risultato contraddittorio.
Allora O deve trovarsi necessariamente sulla retta passante per ZC con la conseguenza che
la retta congiungente O con C passa per M
meglio dei primi tentativi... ma il finale non mi piace tanto. Comunque te la do per buona (con qualche riserva... ).
).
Meno male.
Speravo in questo 6 - - perché tra la rovente assemblea condominiale di questo pomeriggio e l'allarme temperatura ( senza aria condizionata) escogitare altre risposte mi avrebbe mandato in ebollizione il cervello.
Comunque se mi viene qualche idea tra un consuntivo e un preventivo la scriverò.
P.S. i quiz 4 stelle dovresti proporli in inverno.
le temperature dovrebbero scendere... perché non approfittarne per proporre un bel cinque stelle ????!!!!
Va beh, va beh... aspettiamo il fresco