Le soluzioni ai quiz hanno, normalmente, un numero ridotto di lettori. Questa volta, però, vi chiedo di fare un'eccezione e seguire in tanti la dimostrazione passo dopo passo. Questo è l'unico modo per imparare a maneggiare adeguatamente la geometria e renderla piacevole e stimolante. Per aiutare in questa operazione ho svolto TUTTI i passaggi, a costo di rendere più lunga, ma decisamente alla portata di una scuola media superiore, la soluzione.

Il quiz è stato -forse- risolto da Maurizio, ma ho ancora qualche dubbio in proposito. Io seguirò un'altra strada che conferma il detto: "Chi va piano va sano e va lontano". Inoltre scopriremo, insieme, qualche "trucchetto" che viene spesso tralasciato, benché estremamente ovvio.

Buon divertimento!

Prima di iniziare, come si dovrebbe sempre fare negli esercizi geometrici (ma non solo), vediamo di ragionare sul problema e di caratterizzarlo adeguatamente. Vogliamo dimostrare che tre punti sono allineati. In particolare, O, C ed M della Fig. 1.

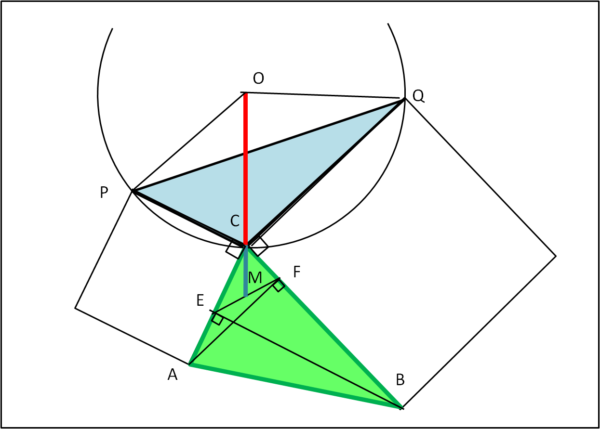
Cosa dobbiamo provare per giungere a questa conclusione? Beh… non è certo difficile: OCM deve essere un angolo piatto, ossia deve essere uguale a 180°.

Dalla figura si vede bene che questo angolo comprende, per costruzione, un angolo di 90° (PCA). Il che ci dice che basta provare che PCO + ACM sia un angolo di 90°.

Ne segue che dobbiamo lavorare su questi due angoli e trovare una relazione  che confermi quanto richiesto.

Spezziamo la dimostrazione in due parti: una dedicata al triangolo ABC, attraverso cui cercheremo di fare intervenire l’angolo ACM e una dedicata al triangolo PCQ, dove cercheremo di legare tra loro gli angoli PCO + ACM, cercando di dimostrare proprio che la loro somma è 90°.

Prima parte

Consideriamo, in Fig. 2, il triangolo ABC da solo.

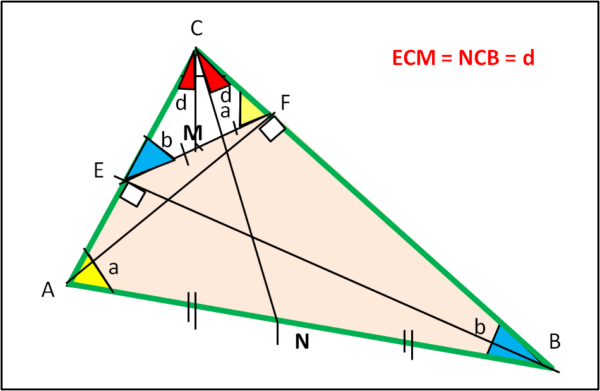
Gli angoli in E e F sono retti per costruzione, da cui segue che il quadrilatero AEFB è ciclico, ossia è inscritto in un cerchio, di cui AB è il diametro. In un quadrilatero ciclico la somma degli angoli opposti è sempre 180°. Ne segue che l’angolo a  (CAB) è supplementare all’angolo EFB. Ma anche l’angolo CFE è supplementare allo stesso angolo, per cui:

CFE = CAB = a

Ragionamento analogo può essere fatto per l’angolo b:

CEF = CBA = b

Consideriamo i due triangoli ABC e CEF. Essi hanno i tre angoli uguali e quindi sono simili. Conduciamo da C le mediane di AB ed EF che incontrano i  lati in N e M. I triangoli EMC e CNB sono ancora simili, per cui:

ECM = NCB = d                …. (1)

Teniamo “al caldo” questo risultato …

 

Seconda parte

Passiamo ora alla Fig. 3

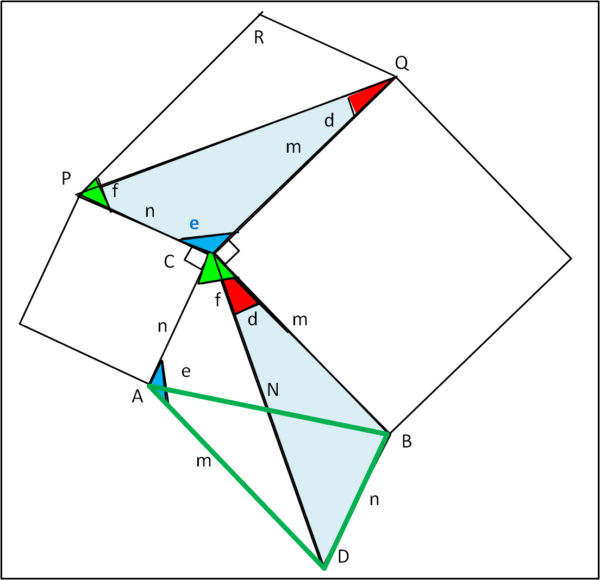
Tracciando le dovute parallele, costruiamo il parallelogramma ACBD. In modo analogo costruiamo il parallelogramma PCQR. Entrambi i parallelogrammi hanno gli stessi lati (m ed n), ma quali sono i loro angoli?

Sappiamo che in un parallelogramma gli angoli adiacenti lo stesso lato sono supplementari, per cui:

RPC + PCQ = 180°

Portiamoci in C e scriviamo:

PCQ + ACB + 90° + 90° = 360°

PCQ + ACB = 180°

ACB e RPC sono supplementari dello stesso angolo PCQ, per cui devono essere uguali:

ACB = RPC = f

Ma lo stesso vale anche per il parallelogramma  ABCD. L'angolo CAD è supplementare di ACB

CAD + ACB = 180°

ma sappiamo anche che:

ACB + PCQ = 180°.

ne segue che

CAD = PCQ = e

I due parallelogrammi sono congruenti avendo lati e angoli congruenti.

Basta, allora, tracciare le diagonali PQ e CD, per concludere che:

PQC = DCB = d

 

Conclusione

Disegniamo la Fig. 4, inserendo quanto dimostrato finora.

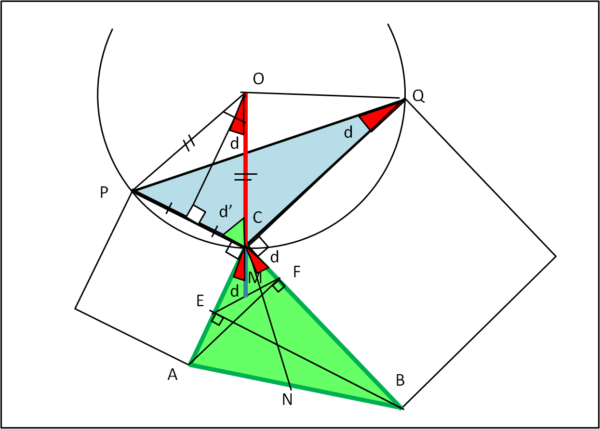
L’angolo al centro POC è doppio dell’angolo alla circonferenza PQC = d. Tracciando la perpendicolare da O a PC , individuiamo l’angolo d'. Possiamo scrivere che:

d’ = 90 – d

ossia:

d’ + d = 90°

Portiamoci nel punto C e sommiamo un po’ di angoli…

OCM = OCP + 90 + ECM

ossia

OCM = d’ + 90 + d

Sappiamo che d + d’ = 90°, per cui:

OCM = 90 + 90 = 180°

In altre parole OCM è un angolo piatto, ossia:

O, C ed M stanno su una stessa retta

CVD