Iniziamo con un "gioco" divertente, ma meno facile di quello che potrebbe sembrare. Esso consiste nell'indovinare un certo poliedro o, solido in genere, attraverso l'ombra che proietta se illuminato da tre direzioni ortogonali tra loro. Un caso piuttosto particolare è già stato trattato durante un quiz dove si notava che il cubo, se visto dalla giusta angolazione, si proietta come esagono. Ma, oggi, andremo molto più in là partendo da qualcosa di estremamente semplice.

Il gioco

In Fig. 1 vediamo due casi veramente banali. Ovviamente, a sinistra, abbiamo un cilindro e a destra una piramide a base quadrata.

Facile? Bene... allora, guardate la Fig. 2.

Ancora più semplice? No, direi proprio di no, in quanto non si tratta di un cubo, ma di qualcosa di ancora più elementare: il tetraedro! Un poliedro platonico che si proietta esattamente come il cubo. E non lo fa solo per una angolazione, ma per tre direzioni ortogonali tra loro, proprio come vuole il nostro gioco.

La dimostrazione di quanto detto è -forse- più difficile del previsto, dato che il tetraedro è un solido che porta a confusione se immaginato in tre dimensioni. Normalmente, si iscrive il tetraedro dentro un cubo, in modo che i suoi vertici coincidano con quattro vertici del cubo e i suoi lati siano le diagonali delle facce del cubo. Io ho pensato a un metodo un po' diverso che penso sia più chiaro nel mostrare la costruzione dell'ombra utilizzando solo due piani tra loro ortogonali. Vediamo come ottenere la nostra ombra "cubica".

Prendiamo il tetraedro e appoggiamo una sua faccia sul piano del foglio da disegno (Fig. 3).

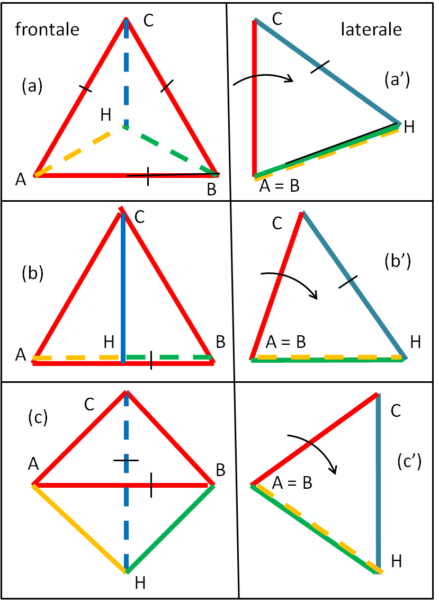
Il triangolo equilatero ABC rimane se stesso con tre suoi lati disegnati in  rosso (a). Dietro questa faccia si nasconde il resto del poliedro. Le linee tratteggiate in blu, verde e giallo vanno a congiungersi nel quarto vertice del poliedro, in H. I lati che conservano le lunghezze originarie sono indicati con un trattino. I tre lati nascosti, visti frontalmente. sono accorciati e hanno la stessa lunghezza

Spostiamoci di 90° verso destra e vediamo come appare il tetraedro (a'). Questa è la proiezione laterale del tetraedro. il segmento rosso corrisponde alla faccia frontale della (a), ma la sua lunghezza è pari all'altezza del triangolo equilatero. L'unico lato che conserva la sua lunghezza originaria è il lato azzurro, dato che risulta perpendicolare alla linea di vista. Ovviamente è inclinato e si congiunge ai lati verde e giallo (sovrapposti) nel punto H.

A questo punto, teniamo fisso il lato AB e ruotiamo il tetraedro attorno ad esso verso destra fino a ottenere la configurazione (b'). Il poliedro mantiene la stessa forma a parte la rotazione. Torniamo alla vista frontale (b). Il triangolo rosso ha la base AB immutata (abbiamo ruotato il poliedro attorno a lui), ma ha gli due altri lati rossi accorciati.

Nella vista laterale (c') il triangolo continua a mantenere la sua forma anche se ruotato ulteriormente attorno ad AB,  mentre la visione frontale (c) presenta un triangolo rosso ABC, decisamente di altezza minore a prima, a cui va aggiunto, in basso, un triangolo esattamente uguale di base AB e vertice H. Quasi magicamente la proiezione frontale, che è poi la nostra ombra, diventa un quadrato, il cui lato è uguale al lato del triangolo equilatero di partenza diviso per radice di 2. Infatti, il lato originario (AB) è proprio la diagonale del quadrato. La lunghezza di CH si è sempre mantenuta e diventa anch'essa diagonale del quadrato.

In realtà, malgrado il tetraedro sia il più semplice dei poliedri platonici o regolari non è di facile "lettura". Per chi avesse ancora dei dubbi consiglio di costruirlo su un foglio di cartoncino, come illustra la Fig. 4.

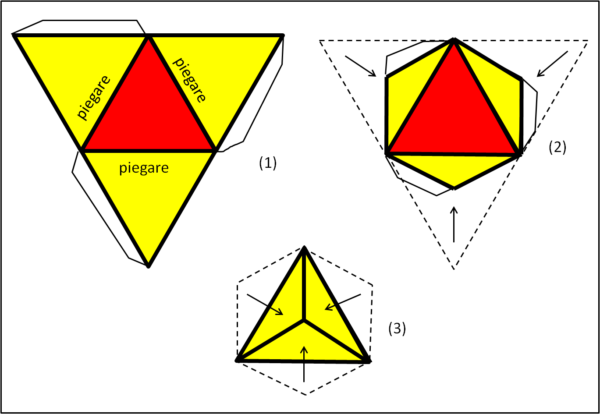
Disegniamo quattro triangoli equilateri, di cui uno centrale e tre sui suoi lati. In pratica, abbiamo un grande triangolo che è formato da quattro triangoli uguali Pieghiamo le facce gialle verso l'alto fino a far combaciare i loro tre vertici ancora liberi. Avere il "modellino" a portata di mano può essere molto utile per verificare le varie proiezioni.

Fino a questo punto abbiamo solo giocato, a parte l'aver dimostrato che tre ombre quadrate possono benissimo essere causate da un tetraedro piuttosto che da un cubo. Iniziamo, allora, un discorso un po' più serio, proprio sfruttando questa uguaglianza di comportamento. In pratica, lavoriamo sul cubo sapendo che i risultati possono poi essere "facilmente" trasportati sul tetraedro.

Il cubo immaginario

Il tetraedro può essere definito come "cubo immaginario", in quanto crea l'ombra di un cubo pur essendo un poliedro completamente diverso. Entriamo, perciò, nel mondo dei cubi immaginari, molto più complesso di quanto possa sembrare.

Iniziamo considerando un vero cubo e proiettiamolo in Fig. 5.

Nessun problema, ovviamente, dato che il cubo immaginario è proprio un ... cubo. Tuttavia, possiamo dividere il nostro cubo in otto cubi più piccoli ed eliminare il cubetto in alto a sinistra, come mostra la Fig. 6.

E' cambiato qualcosa nelle ombre? Assolutamente no. Cerchiamo allora di spingerci più in là ed eliminare anche il cubetto in basso a destra (Fig. 7).

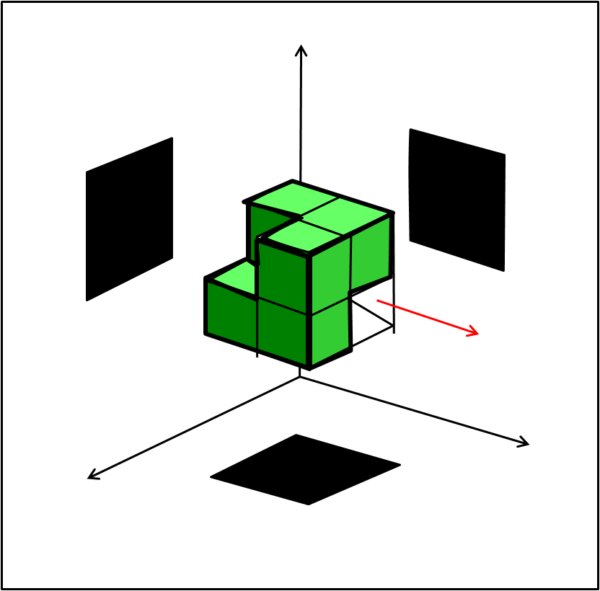
Ottimo! Le ombre restano sempre le stesse dato che i sei cubetti sono sufficienti a bloccare la luce in tutte e tre le direzioni.

Possiamo fare di meglio? A prima vista sembrerebbe di no, ma riflettiamo un attimo e agiamo come mostra la Fig. 8.

Abbiamo eliminato altri due cubetti e invece di un cubo vi è la metà di esso. Una delle ombre rimane inalterata, mentre le altre due mostrano chiaramente l'inutilità della manovra appena compiuta, presentandosi come due rettangoli.

Un momento, un momento... Spostiamo due cubetti come mostra la Fig. 9...

I quattro cubetti si toccano, a due a due, lungo uno spigolo. Qualcosa è cambiato. Anche una seconda proiezione è diventata un quadrato completo. Non è il momento di fermarsi, ma di proseguire...

Ci vuol poco per arrivare alla situazione di Fig. 10.

I due cubetti superiori vengono spostati di una posizione verso destra. Il nostro cubo sembra distruggersi del tutto, dando luogo a due ombre piuttosto strane e più lunghe di quelle iniziali E invece no, siamo in una situazione molto favorevole per riottenere le ombre quadrate. Basta, infatti, spostare il cubetto in alto a destra verso sinistra, riportandolo nelle condizioni iniziali (Fig. 11).

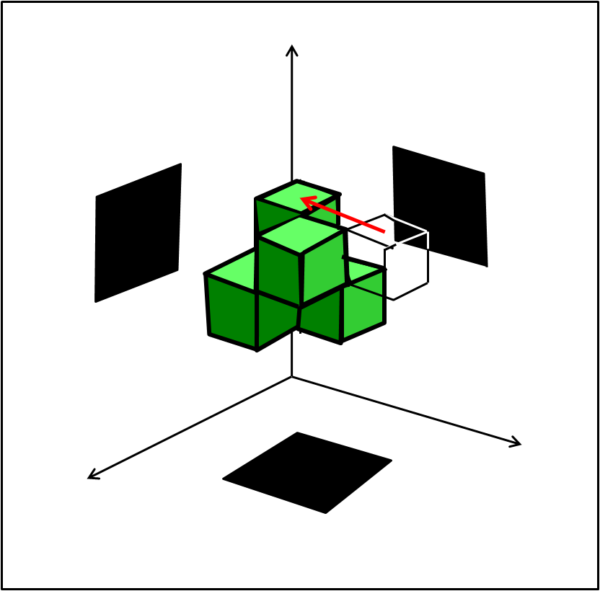
Ancora una volta, come per magia, le nostre ombre sono ridiventate quadrati. E abbiamo utilizzato solo quattro cubetti invece che gli otto originari.

Non ci si può stupire se il poliedro finale (non certo regolare) prenda il nome di cubo immaginario. Esso è tutto fuorché un cubo, ma le sue ombre sono esattamente uguali. In particolare, la configurazione ottenuta è quella "minimale", in quanto vi è uno e un solo cubo a creare ombra nelle varie proiezioni. Una configurazione minimale si può anche ottenere con una divisione in un numero maggiore di cubetti, come mostra la Fig. 12.

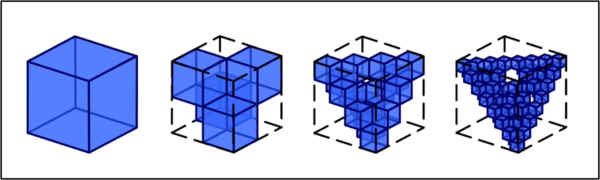
Siamo arrivati al primo punto chiave: un cubo immaginario può presentare al suo interno una serie di cubetti "vuoti", ma la sua ombra resterà continua e quadrata. Il secondo punto chiave è ancora più importante: possiamo tranquillamente sostituire ogni cubetto della nostra costruzione con dei semplici cubi immaginari come il tetraedro. Un insieme, disposto adeguatamente, di piccoli tetraedri può comportare delle ombre che appaiono come quadrate. Non solo, però, anche una forma generale a tetraedro può ovviamente essere divisa in tetraedri più piccoli, sufficienti a farlo diventare un cubo immaginario (Fig. 13).

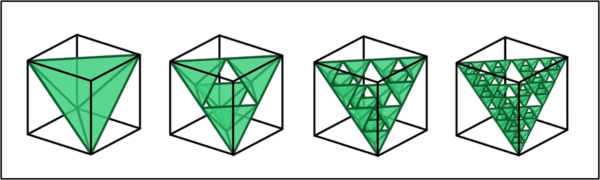
Il tetraedro frattale  di Sierpinski

A questo punto facciamo un piccolo salto e andiamo a presentare un triangolo molto particolare, chiamato triangolo di Sierpinski, una celebre figura frattale. Non è difficile costruirla... basta commentare la Fig. 14.

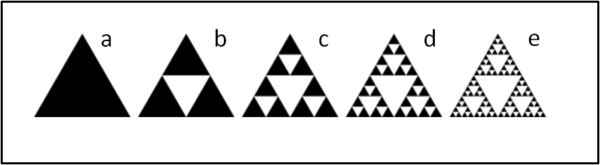
Prendiamo un triangolo equilatero (a). Costruiamo un nuovo triangolo equilatero al suo interno con vertici nei punti medi dei lati del triangolo iniziale e lo rimuoviamo del tutto, lasciando un buco centrale (b). Per ognuno dei tre triangoli rimasti ripetiamo l'operazione (c). Basta ripetere ancora due volte la divisione e si arriva alla (e). Siamo ormai di fronte a un triangolo, costruito come un frattale, che sembra fatto di... vuoto. La faccenda, però, può espandersi alle tre dimensioni e una costruzione simile può essere fatta su un tetraedro, come mostra la Fig. 15.

La conclusione è abbastanza ovvia: un tetraedro di Sierpinski è composto da tanti tetraedri  di dimensioni sempre più piccole. Un tetraedro fatto praticamente di vuoto... ma -attenzione!- abbiamo visto che un tale solido proietta ombre quadrate, come mostra la Fig. 16.

Le mani sono quelle del Prof. Hideki Tsuiki dell'Università di Kyoto, un matematico estremamente esperto in cubi immaginari, il più famoso dei quali è proprio il tetraedro di Sierpinski.

Questi cubi immaginari si trovano anche in vendita a poche decine di euro... mi sa che me ne comprerò uno