Categorie: Matematica
Tags: circocentro geometria incentro quiz tangenza
Scritto da: Vincenzo Zappalà
Commenti:36
Un quiz veramente diabolico... ***** (con correzione della Fig. 1)
Penso che questo problema geometrico sia -forse- il più "diabolico" che abbia mai affrontato., benché , per la sua soluzione, basti solo la geometria "elementare" (roba da liceo e niente di più ...). Ammetto, però, che dopo un po' la testa sembra andare in pallone e si scivola verso una confusione non indifferente. Insomma: nervi saldi, ragionamento e tenere sempre sotto controllo i vari passaggi. Ovviamente, possono esistere metodi alternativi, più rapidi ed eleganti...
La formulazione del problema è piuttosto accattivante e la descriviamo mediante la Fig. 1:
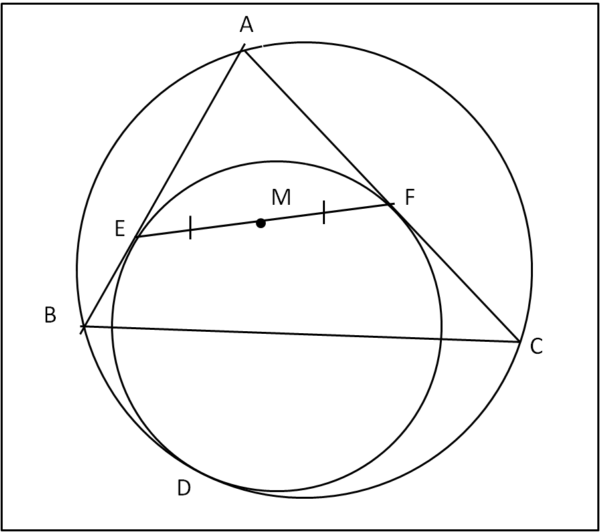
Consideriamo un triangolo qualsiasi ABC. Tracciamo il suo cerchio circoscritto e un cerchio che sia tangente internamente ai lati AB e AC, nei punti E ed F, e che sia tangente internamente al cerchio circoscritto ad ABC nel punto D. Uniamo E con F e segniamone il punto di mezzo M.
Dimostrare che M è l'incentro del triangolo ABC, ossia il centro del suo cerchio inscritto.






36 commenti
Sarebbe di aiuto se spiegassi la costruzione progressiva della figura di partenza dopo avere disegnato il triangolo ABC e il suo cerchio circoscritto.
Con quali passaggi è stato tracciato il cerchio interno? Come hai individuato il suo centro?
La descrizione di come costruire la figura iniziale, nel testo del quiz, dice di assegnare per primo il triangolo ABC , poi il cerchio circoscritto e infine il cerchio interno.
Per ottenere la stessa figura mi sembra più facile questa diversa sequenza:
Fisso un punto O e, con centro in esso, traccio un cerchio di raggio arbitrario
Poi scelgo un qualsiasi punto sulla circonferenza e lo chiamo D
Collego D con O e scelgo un punto qualsiasi R su questo segmento
Con centro R traccio il cerchio interno che passa per D e ovviamente tangente a quello esterno
Scelgo un punto A sulla circonferenza esterna e da esso traccio le tangenti alla circonferenza interna
Chiamo E ed F i punti di tangenza
I punti di intersezione tra le due tangenti e la circonferenza estera sono i punti B e C che chiudono il triangolo ABC
Collego tra loro E ed F e trovo il punto medio M.
In questo modo ho il triangolo ABC, il suo cerchio circoscritto, il cerchio interno tangente, i punti EF tra loro collegati e il punto medio M, ossia la figura del testo.
(segnalo una piccola correzione da fare al testo del quiz : il cerchio interno è tangente ai lati AB e AC e non AB e BC)
Adesso, se volessi ripetere la costruzione per la coppia di lati CA e CB (invece che per la coppia di lati AB e BC come ho fatto ora) dovrei disegnare un cerchio che sia tangente internamente ai lati AB e BC, nei punti G ed H, e che sia tangente internamente al cerchio circoscritto ad ABC nel punto L .
La sequenza è quindi proprio quella indicata nel testo del quiz, ossia, il nuovo cerchio interno va costruito avendo già fissato il triangolo ABC e il suo cerchio circoscritto.
Questo mi sembra più difficile e mi chiedo perché hai indicato proprio questa sequenza (che alla fine porta al medesimo risultato di quella che ho descritto)?
Ma mi chiedo soprattutto quali passaggi hai seguito per realizzarla.
In realtà il cerchio tangente ai due lati e al cerchio circoscritto è un dato del problema. Io l'ho costruito per via grafica in modo molto semplice come mostra la figura che segue
Il centro R deve trovarsi lungo la bisettrice AK. Traccio qualche cerchio con raggio crescente fino a che non trovo quello che è tangente anche al cerchio circoscritto. Non penso sia difficile trovare anche una relazione geometrica unica, ma per il nostro problema basta e avanza che si dia per acquisito. E' inutile complicare ancora di più la faccenda. Comunque quello che chiedi tu potrebbe essere un altro quiz...
Non vedo perché dovrei cambiare la presentazione del quiz. Ciò che bisogna fare per la costruzione del problema è più che chiaro ed è tutto quello che sappiamo. Si prende un triangolo, si disegna il suo cerchio circoscritto e poi si costruisce il triangolo tangente in modo grafico (ma poco importa dato che esso va inteso come acquisito e si sa che ha le tre tangenze) con un qualsiasi metodo grafico. Fatto questo si individua il punto M. Perché mai si dovrebbe cambiare questa presentazione? Ormai hai tutto ciò che serve: tre punti di tangenza, un punto medio M tra due di questi e il punto D di tangenza tra due cerchi.
Non cincischiamo e affrontiamo il vero problema!
Non intendevo assolutamente dire che si deve cambiare nulla.
Ho solo chiesto come avevi fatto a fare la costruzione per due motivi:
1 perché era funzionale a una soluzione che avevo in mente.
2 perché, avendo seguito la via grafica anche io, non la trovavo del tutto soddisfacente.
Mi è ben chiaro che, avendo la figura già fatta non è indispensabile sapere come è stata costruita ma, nella tradizione del blog, è importante capire tutti i passaggi
Oggi non ho tempo di cincischiare sul quiz, se domani nessuno lo avrà risolto, prometto di dedicarmici un po'.
Pensavo di avere scritto che la figura iniziale presentava degli errori (il punto R, ad esempio). Probabilmente nel pasticcio nato a seguito della "caduta" di Aruba, il commento non è stato inviato. In ogni modo, avevo corretto la figura già ieri... Penso di dare la soluzione con tutti i passaggi anche i più elementari, ma non pensavo che bisognasse anche spiegare la costruzione di un qualcosa che era stato perfettamente definito. Comunque, ora l'ho aggiunto nei commenti.
A questo punto penso che si possa veramente "ricominciare da tre"...
AM è la bisettrice di BAC perché il triangolo AEF è isoscele
ipotesi: M è l'incentro
procedo con la seconda figura aggiungendo le linee in colore blu
traccio la retta CM (bisettrice presunta di ABC) e la sua perpendicolare nel punto M individuando E' F' sui due lati BC e AC
Traccio le perpendicolari ai due lati nei punti E'F' nel loro punto di intersezione trovo trovo R'
R' è sulla retta CM (bisettrice presunta)
Collego O, centro del cerchio circoscritto ad ABC, al punto R' e sul prolungamento interseco (perpendicolarmente) il cerchio circoscritto nel punto D'
Per i tre punti E'F'D' passa una sola circonferenza, di centro R', tangente al cerchio esterno in D' e ai due lati in E' e F'
La disegno, sempre in colore blu.
Il risultato finale tracciato in blu, raffigura la medesima costruzione, descritta nel testo del quiz. eseguita inizialmente per i due lati del triangolo AB AC e dalla quale avevamo ottenuto la bisettrice di ABC
Quindi, in base a tale costruzione, CM risulta essere effettivamente la bisettrice di ABC
Questo conferma l'ipotesi che M è l'incentro.
Vedo che stai riflettendo sulla soluzione diabolica al quiz diabolico ...In realtà non abbiamo nessuna prova che la distanza R'D' sia uguale a R'E' e R'F' ...
E' lo stesso problema che mi ponevo all'inizio. La tua soluzione grafica va bene per fare la figura iniziale ma adesso dovremmo garantire rigorosamente che le misure sono congruenti.
Scusa Mau, ma ancora una volta temo che la figura faccia accettare qualcosa come dato di fatto.
Tu tracci la retta CM, dove M è un punto qualsiasi che sta sulla bisettrice di BAC. Unisci M con E' e F' che stanno sul triangolo di partenza. Poi tracci le perpendicolari ai due lati in E' e F'. Il loro punto d'incontro è R'... ma chi mi dice che R' stia sulla retta CM? Nella figura, ad esempio, R'E' > R'F'. Come fa R' ad essere centro del cerchio con cui tu concludi?
Un consiglio... Cercare la relazione che mi dica che cosa caratterizzerebbe M se fosse l'incentro. E poi cercare di verificarla. E' lo stesso problema della volta scorsa... partire con un qualcosa di preciso da dimostrare.
In altre parole, Mau...
tu ipotizzi che R' stia sulla retta CM ipotizzando che CM sia bisettrice, ma facendo questo è ovvio che alla fine M risulti l'incentro, dato che è l'intersezione di due bisettrici, di cui una, però, è, per quanto ne sappiamo fasulla. Se CM è bisettrice il risultato è immediato, ma non si dimostra niente, perchè M è stato costruito in altro modo.
Allego la figura che avevo mandato prima con una lettera sbagliata...
Se provi a evidenziare il testo che segue i 3 puntini (sono righe non visibili perché scritte in bianco) nel mio precedente commento (ore 17,12) vedrai che ne ero ben consapevole.
Quello che mi interessa maggiormente in questo momento, a lato di questo quiz, è trovare il modo di costruire il cerchio interno non per tentativi ma seguendo una precisa logica.
A me sembra cosa secondaria... comunque il tuo approccio ipotizza che CM sia bisettrice e questo è del tutto arbitrario. Provo anch'io a risolvere il problema della costruzione che, però, potrebbe essere fatta attaverso l'incentro. Cosa, questa, che non cambia minimamente il problema. Ci sono vari modi per caratterizzare l'incentro e qui sta il punto chiave iniziale.
Le caratteristiche dell'incentro sono sostanzialmente di appartenere alle tre bisettrici e di essere equidistante dai tre lati (per i quali passa quindi il cerchio inscritto ) Al momento non ne ricordo altre.
Vorrei però proporti questo ragionamento...
Eseguiamo la stessa costruzione descritta nel quiz sulla coppia di lati AC e CB e troviamo oltre alla bisettrice rossa di BAC anche la bisettrice blu di BCA
indico con M il punto medio nella prima costruzione e con M' quello nella seconda.
Se M ed M' coincidono quel punto è l'incentro I
Domandiamoci quindi “Può il punto M' non coincidere con il punto M?”
Disegniamo la situazione nella ipotesi che M e M' siano coincidenti tra loro e con I (incentro)
Allontaniamoci ora da questa ipotesi:
Facciamo slittare M sulla bisettrice a cui appartiene (rossa) verso il punto A e facciamo slittare M' sulla bisettrice a cui appartiene (blu) verso il punto C
In questa Figura 4, M e M' non sono più sovrapposti a I né sono sovrapposti tra loro. Continuano a trovarsi sulle rispettive bisettrici
I punti E ed F sono rimasti fissi e ora M non è più allineato con essi.
Allo stesso modo i punti E' e F' sono rimasti fissi, e quindi non sono più allineati con M'
Dobbiamo quindi traslare anche i segmenti EF e E'F' in modo che passino per M e M'.
Facendo questo spostamento, però, le loro intersezioni con i lati si spostano e anche le lunghezze dei segmenti cambiano.
Possiamo concludere che l'ipotesi di M e M' non coincidenti genera in ogni caso delle incongruenze.
Solo ammettendo che M ed M' coincidono possiamo evitarle. Ma la coincidenza di M e M' in un unico punto I, qualifica tale punto come Incentro del triangolo ABC.
per quanto riguarda la costruzione ( grazie per cercarla anche tu) si tratta di inserire un cerchio non in un triangolo ma in un triangolo mistilineo in cui ci sono due lati rettilinei ad esempio AB e AC e un arco di cerchio che li congiunge (andando da B a C. Occorrerebbe prolungare i lati rettilinei e come terzo lato avresti una delle tangenti sull'arco di cerchio che va a intersecare i prolungamenti del lati. Ma in quale punto collocare questa tangente sull'arco?
Il punto è ovviamente il punto D, che deve distare dal centro esattamente come le perpendicolari ai lati.
Non mi convince... in quanto non sfrutta i dati del problema che sono quelli relativi a un solo punto M trovato in un certo modo. Non possiamo ipotizzarlo come incentro e verificare possibili incongruenze. Bisogna partire da quei dati e dimostrare la tesi. Si può fare... basta trovare una nuova caratteristica dell'incentro.
Affrontiamo il problema di petto senza girargli troppo attorno...
Pensa a una caratterizzazione dell'incentro nel caso generale e poi cerca di verificarla nel caso in questione, partendo solo da un cerchio inscritto e da un punto M.
Parliamoci chiaro: per quale motivo M e M' devono coincidere? La costruzione con i cerchi mistilinei non assicura questo, ma potrebbe portare a due punti diversi senza creare incongruenze se M non fosse l'incentro.
Risolvo la questione prima di andare a letto. I tre punti M1, M2 e M3 sono costruiti sfruttando tre cerchi diversi. Non vi è nessun motivo perché essi coincidano. Se si dimostrasse che coincidono allora sarebbero l'incentro, ma non vi è nessuna incongruenza a lasciarli separati, vista la loro costruzione che niente ha a che fare con la definizione di incentro. Il lavoro è ancora lungo...
Prima di andare a letto, aggiungo una cosa...
Nella tua ultima dimostrazione, tu trovi tre punti M1, M2 e M3. Essi sono costruiti attraverso il cerchio mistilineo (chiamiamolo così) e possono benissimo non coincidere. Niente li obbliga a essere l'incentro, ma solo tre punti qualsiasi che verificano le condizioni di punto medio di tangenti a tre cerchi diversi. Che essi debbano coincidere e diventare l'incentro è un'ipotesi non obbligatoria e nemmeno incongruente.
Tra parentesi ho trovato la costruzione del cerchio mistilineo. Ovviamente si avvale dell'incentro, ma questo è sempre costruibile per un triangolo. La coincidenza tra M e l'incentro è cosa da dimostrare. Domani vado più a fondo, ma sappi che esiste!
Probabilmente la caratteristica dell'incentro da cui occorre partire è che divide ciascuna bisettrice in due parti
Il rapporto tra le due parti e il medesimo che intercorre tra uno dei due lati del triangolo e la parte di lato tagliato dalla bisettrice che si trova dalla sua parte.
Nella figura di partenza traccio la bisettrice di BAC fino a tagliare il lato BC nel punto N
Se M fosse l'incentro (da dimostrare) avrei AM ; MN = AB; BN e anche = AC:CN
Quindi se si prova l'esistenza di queste uguaglianze allora M è l'incentro.
Torniamo al problema iniziale.
Diamo per acquisito il cerchio tangente ai lati del triangolo e al cerchio circoscritto al triangolo. Esiste una costruzione che, però, comporta proprio di utilizzare ciò che vogliamo dimostrare. Tuttavia, sapendo che questo cerchio deve esistere ed è anche unico per un dato vertice, niente ci vieta di prenderlo come dato del problema, costruendolo "per tentativi" come avevo fatto in un commento precedente. L'importante è che questo cerchio sia tangente ai lati e questo fatto niente ha a che vedere con l'incentro.
D'altra parte, è stato presentato alle olimpiadi di matematica e l'ipotesi che faccio io era stata fatta anche in quella sede.
Oggi ho parecchie cose da fare, tra cui una conferenza sulla MQ. Ne segue che difficilmente potrò seguire la discussione con Mau e - magari- anche con qualche altro audace (lo spero vivamente).
Grazie per la precisazione e buona conferenza
Penso di non aggiungere commenti nel corso della giornata, sia perché di domenica è meglio lasciar stare le cose diaboliche, sia perché in questo modo non sarai tentato di andare a vedere ogni tanto sul blog.
Mi ero perso il commento di stamattina (8:27).
Tu scrivi:
Nella figura di partenza traccio la bisettrice di BAC fino a tagliare il lato BC nel punto N
Se M fosse l'incentro (da dimostrare) avrei AM ; MN = AB; BN e anche = AC:CN
Quindi se si prova l'esistenza di queste uguaglianze allora M è l'incentro
Vorresti spiegare da dove e come saltano fuori quei rapporti e uguaglianze? Il problema è già complesso e ogni passaggio deve essere spiegato con la geometria elementare.
Ecco la risposta alla tua richiesta.
Figura 1
Il triangolo ABC è scomponibile nei due triangoli ABN e ANC, come si vede nella figura 1.
Essi hanno la medesima altezza h (in colore blu), quindi le loro aree staranno nel rapporto delle rispettive basi BN e NC.
area ABN : area ANC = BN : NC
Ora tracciamo da N le perpendicolari ai due lati AB e AC, ossia le altezze dei due triangoli ABN e ANC, relative rispettivamente ai lati AB e AC.
Queste altezze h1 e h2 ( in colore verde) sono di uguale misura per la nota proprietà della bisettrice.
Le aree dei due triangoli ABN e ANC, avendo anche in questo caso la medesima altezza, staranno tra loro nel rapporto delle rispettive basi , che ora sono AB e AC, lati del triangolo ABC.
area ABN : area ANC = AB : AC
Pertanto , per la proprietà transitiva, BN : NC = AB : AC
Questo ragionamento costituisce il "Teorema della bisettrice"
Vediamo ora a quali conclusioni si può arrivare applicandolo alle tre bisettrici di un triangolo
Osservando il triangolo ABC e le sue tre bisettrici che si intersecano in un unico punto M, ossia nell'incentro, si vede che ciascuna di esse è divisa in due parti.
Applichiamo il teorema della bisettrice alla prima bisettrice AN', divisa in AM+MN', come si può vedere nella figura 2, triangolo ABN
AM:MN' = AB:BN' = AC:CN'
analogamente, per la seconda bisettrice BN'', divisa in BM+MN''
BM:MN'' = BA:AN'' = BC:CN''
e infine, per la terza bisettrice CN''' , divisa in CM+ MN'''
CM:MN''' = CB:BN''' = CA:AN'''
Mi sono accorto che nei dati del problema si dà per acquisito che esista il cerchio mistilineo. Ciò comporta che non è detto che il suo centro stia sulla bisettrice di BAC... Va dimostrato anche quello (anche se non è difficile).
Tracciando le perpendicolari ai lati da E e F trovo il centro del cerchio. la distanza del centro dai due lati è la stessa quindi se collego il centro al vertice A ho la bisettrice di BAC
non fa una grinza... perfetto.
Siamo sicuri che M stia sulla bisettrice? Dimostrazione banalissima...
La distanza di E da A è uguale alla distanza di F da A, essendo punti di tangenza alla circonferenza interna
Il segmento EF è la base di un triangolo isoscele EAF, la cui altezza passa per il punto medio M .
Tale altezza divide in due parti uguali l'angolo EAF ed è quindi la bisettrice.
benissimo... ora proseguiamo
In questa figura appaiono i punti principali che possiamo individuare.
La coppia verde individua il centro R del cerchio interno che passa per D (punto tangenza tra i due cerchi)
La coppia centrale, viola, passa per i punti medi dei lati AB e BC e individua il centro O del cerchio esterno, circoscritto ad ABC e passante per D
La terza coppia in rosso ha incrocio nel punto M che appartiene alla bisettrice blu. Le due distanze dai lati AB e BC sono uguali,
La bisettrice contiene i punti A , M, R e N, quest'ultimo è l'intersezione con il lato opposto ad A, BC
I punti O R e D sono allineati
Abbiamo la certezza, data dal testo, che E F D sono punti equidistanti da R e tangenti nei punti di contatto rispettivamente con i lati AB , BC e con il cerchio circoscritto.
Il punto N è equidistante da E e da F, ma non sembra rilevante al fine di dimostrare che M è l'incentro.
Per quale motivo NE = NF ?
Pensiamo più agli angoli che ai segmenti...
Non volendo prolungare l'attesa dei lettori che desiderano conoscere la soluzione, mi astengo da altri commenti.
Se mai trovassi una soluzione alternativa a quella che verrà pubblicata la pubblicherò a mia volta nei commenti
Ho visto il tuo commento, quasi contemporaneo al mio, e per non lasciare domande senza risposta , dico che il motivo per cui NE = NF è dato dal primo criterio di congruenza dei triangoli.
Tale criterio dice che due triangoli sono congruenti se hanno congruenti due lati e l'angolo compreso.
RE e RF sono congruenti, RN altrettanto in quanto condiviso, e gli angoli tra questi lati sono uguali.
OK, perfetto... cerchiamo sempre di spiegare le conclusioni in modo completo (per quanto possibile). No, anche a me non sembra cosa importante ai fini della tesi.