Teorema della bisettrice

In un triangolo i lati adiacenti (come AB e AC) stanno tra loro come le parti distinte dalla bisettrice sul lato opposto (come BN e NC)

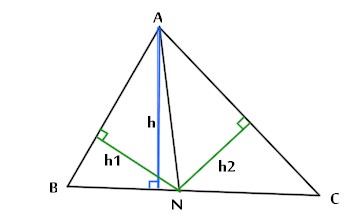
Figura 1

Il triangolo ABC è scomponibile nei due triangoli ABN e ANC, come si vede nella figura 1.

Essi hanno la medesima altezza h (in colore blu), quindi le loro aree staranno nel rapporto delle rispettive basi BN e NC.

area ABN : area ANC = BN : NC

Ora tracciamo da N le perpendicolari ai due lati AB e AC, ossia le altezze dei due triangoli ABN e ANC, relative rispettivamente ai lati AB e AC.

Queste altezze h1 e h2 ( in colore verde) sono di uguale misura per la nota proprietà della bisettrice.

Le aree dei due triangoli ABN e ANC, avendo anche in questo caso la medesima altezza, staranno tra loro nel rapporto delle rispettive basi , che ora sono AB e AC, lati del triangolo ABC.

area ABN : area ANC = AB : AC

Pertanto , per la proprietà transitiva, BN : NC = AB : AC

Come si intendeva dimostrare.

Vediamo ora a quali conclusioni si può arrivare  applicandolo alle tre bisettrici di un triangolo, nel seguente corollario:

In un triangolo l'incentro M divide ciascuna bisettrice ( come CN''') in due parti (come CM e MN''') che stanno tra loro nello stesso rapporto che esiste tra un lato adiacente  (come AC) e la parte di lato opposto staccata dalla bisettrice (come AN''')

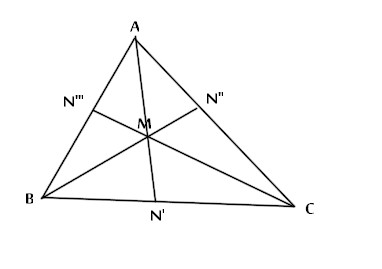Figura 2A

Osservando il triangolo  ABC  e le sue tre bisettrici che si intersecano in un unico punto M, ossia nell'incentro, si vede che ciascuna di esse è divisa in due parti.

Applichiamo il teorema della bisettrice alla prima bisettrice AN', divisa in AM+MN', come si può vedere nella figura 2, triangolo ABN

AM:MN' = AB:BN' = AC:CN'

analogamente, per la seconda bisettrice BN'', divisa in BM+MN''

BM:MN'' = BA:AN'' = BC:CN''

e infine, per la terza bisettrice CN''' , divisa in CM+ MN'''

CM:MN''' = CB:BN''' = CA:AN'''