Questo articolo è inserito in Cinematica

 

Devo ammettere che la mia passione per la geometria ha decisamente "infestato"  le pagine del nostro Circolo. E' ora di cambiare un po' linea, venendo forse incontro a molti tra i silenziosi. Per un po' niente quiz diabolici o cose del genere (magari solo di tanto in tanto).Torniamo alla fisica, che sicuramente ha maggiori riscontri nella vita di tutti i giorni. In particolare alla fisica classica, ancora in grado di spiegare la maggior parte degli eventi che ci circondano.

Iniziamo con la parte più semplice, la cinematica, ossia quella parte della meccanica che descrive e risolve problemi legati al moto dei corpi, senza interessarsi alle cause che li hanno prodotti. Anch'essa può presentare esercizi non banali, soprattutto se si entra nel campo dei moti di rotazione. Cominceremo, però, dai moti rettilineo uniforme e uniformemente accelerato, che si basano essenzialmente su poche formule, facilmente dimostrabili, che abbisognano solo di spazio percorso, di tempo, di velocità e accelerazione. Richiamiamo le poche formule fondamentali, ripresentando, prima, la loro determinazione ottenuta senza bisogno di derivate e integrali. Un argomento questo che avevo trattato nel corso di Matematica e che preferisco riproporre per intero. Ricordiamo solo che le operazioni relative al calcolo di  velocità e accelerazione sono in pratica delle derivate (variazioni di una certa grandezza a seguito della variazione di un'altra), mentre quelle inverse sono legate strettamente all'operazione di integrazione, ossia alla risoluzione di equazioni differenziali. Tuttavia, se non si vuole andare troppo in là, non vi è nessun bisogno di fare ricorso a questi concetti.

Le basi della cinematica

Non posso certamente presentarlo come un quiz… Tuttavia, facciamoci la domanda: “Come si calcola l’aera di un rettangolo?”. La risposta è corale: “Base per altezza o, più semplicemente, lato per lato”. E l’area di un triangolo qualsiasi? Ovvio anche questo: “Base per altezza diviso  due”. E quella di un trapezio? “Somma delle basi per altezza diviso due”. Insomma, su queste cose siamo sicuramente preparati…

No, non voglio prendervi in giro, ma lasciatemi fare la Fig. 1, relativa al rettangolo. Forse la figura più facile che abbia mai presentato… tuttavia, ci verrà molto utile. Abbiamo utilizzato gli assi cartesiani e tracciato due segmenti paralleli agli assi x e y. Il nostro rettangolo OABC ha un lato uguale a x e l’altro uguale a y e la sua area è xy. Insomma, banalità, veramente banalità.

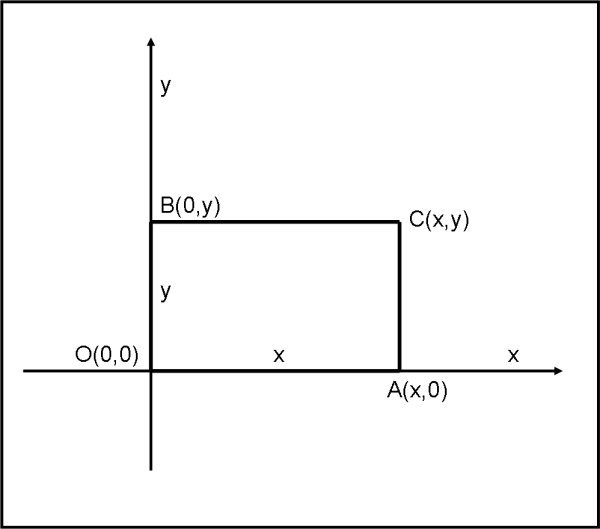
Per rispondere a coloro che vorrebbero vedere chiaramente i legami tra operazioni matematiche e/o geometriche e la fisica applicata, utilizziamo, nuovamente la Fig. 1 (chiamiamola Fig. 2 e ridisegniamola), dove al posto della x inseriamo la variabile t e al posto della y la variabile v. I simboli usati non sono casuali, ovviamente, e sappiamo bene a cosa corrispondono: t rappresenta il tempo e v la velocità. Facciamo, allora, un piccolo salto indietro e vediamo a cosa corrisponde fisicamente la Fig. 2. Beh, non è certo difficile, essa rappresenta il moto di un oggetto con velocità costante v₀.

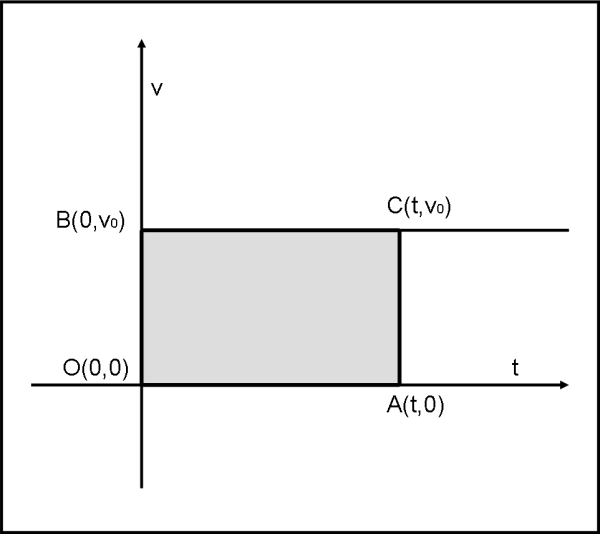
Il grafico, infatti, ci dice che qualsiasi sia il tempo t della misura, la velocità del corpo è sempre la stessa. E’ una situazione così banale? Assolutamente no, dato che siamo nel caso di oggetti che si muovono con velocità costante, ossia di moto rettilineo uniforme. Vi sembra poco? Accidenti, sicuramente no, dato che tutta la relatività ristretta si occupa solo di sistemi di riferimento che seguono questa regola. La Fig. 2 è, quindi, una rappresentazione fondamentale della fisica e non certo un gioco da bambini! Non facciamoci ingannare dalla semplicità e ricordiamo sempre che la Natura lavora in modo semplice.

Come si rappresenta quanto appena detto in un diagramma spazio-tempo? Lo vediamo immediatamente nella Fig. 3, dove gli assi rappresentano, adesso, proprio lo spazio s e il tempo t.

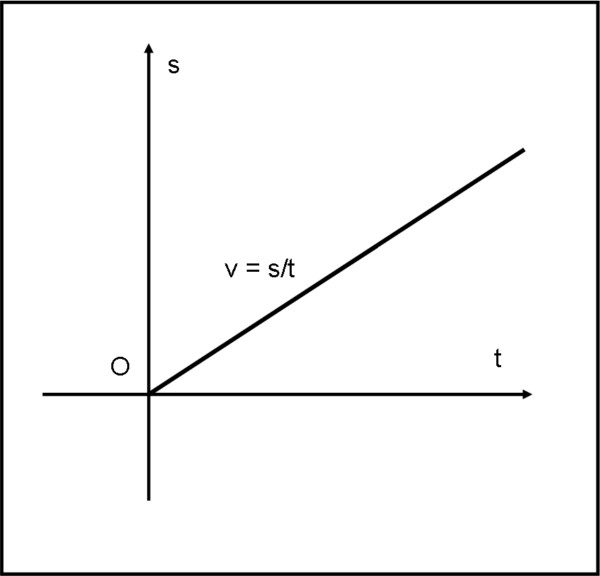
In questo tipo di diagramma, la retta rappresenta proprio lo spazio percorso al passare del tempo. Abbiamo una retta per il semplice fatto che la velocità è costante ed è descrivibile con la pendenza della retta, ossia con il coefficiente angolare. Essendo questa velocità costante possiamo anche scrivere che la velocità non è altro che il rapporto tra qualsiasi s e il t corrispondente e, quindi:

s/t = v

e, ovviamente:

s = vt

Leggiamo questa formuletta in modo elementare:

lo spazio percorso dal corpo è uguale al prodotto tra la velocità (costante) e il tempo trascorso.

Guarda caso è una definizione che ci ricorda estremamente bene l’area di un rettangolo: lato per lato, che in questo caso diventa tempo per velocità.

Lo spazio percorso da un oggetto in moto rettilineo uniforme è dato dall’area del rettangolo che si ottiene utilizzando la Fig. 2. In parole più costruttive, per conoscere lo spazio percorso da un corpo che si muove con velocità v, basta calcolare l’area del rettangolo che ha per lati il tempo trascorso e la velocità costante.

Sembrerebbe una sciocca e inutile conclusione, ma, in pratica ci dice che se conosciamo la velocità è possibile fare il contrario di quello che si fa normalmente in cinematica, quando  si conosce lo spazio percorso nell’unità di tempo e si calcola le velocità. Adesso, invece, partendo dalla velocità ricaviamo lo spazio percorso.

Andiamo avanti con la cinematica elementare e immaginiamo di avere un moto uniformemente accelerato. Cosa vuol dire? Presto detto: la velocità varia in modo uniforme mentre l’accelerazione è costante.

Divertiamoci ancora un poco con i nostri grafici elementari e costruiamo la Fig. 4. Accidenti… ma è sempre la stessa. In realtà no, dato che al posto della velocità c’è adesso l’accelerazione in funzione del tempo. L’accelerazione è però una costante e possiamo calcolare facilmente l’area del rettangolo grigio. Essa è data da at.

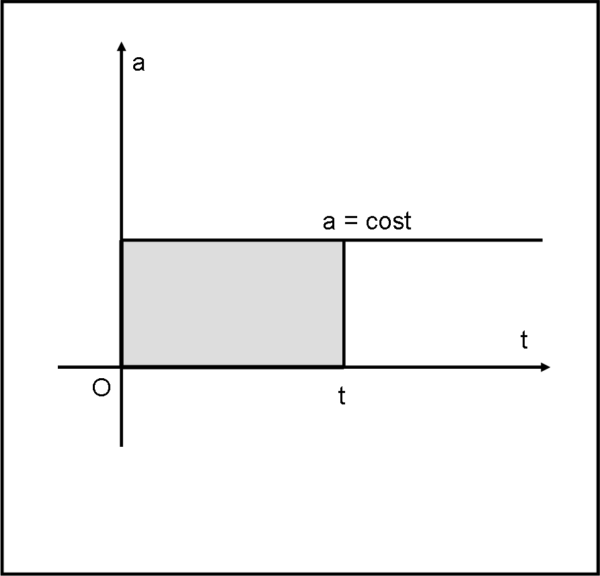
Ma sappiamo molto bene cosa vale at quando a è una costante:

a = v/t

v = a t

Come potevamo facilmente dedurre subito, l’area del rettangolo che ha come lati l’accelerazione e il tempo ci regala la velocità.

Possiamo quindi facilmente passare da accelerazione a velocità calcolando l’area del rettangolo, analogamente a quanto abbiamo fatto per velocità e spazio nel caso di moto uniforme.

Il giochino è veramente divertente e vediamo se, anche in questo caso, è possibile arrivare fino allo spazio percorso. Non ci resta che disegnare di nuovo in Fig. 5 la velocità in funzione del tempo.

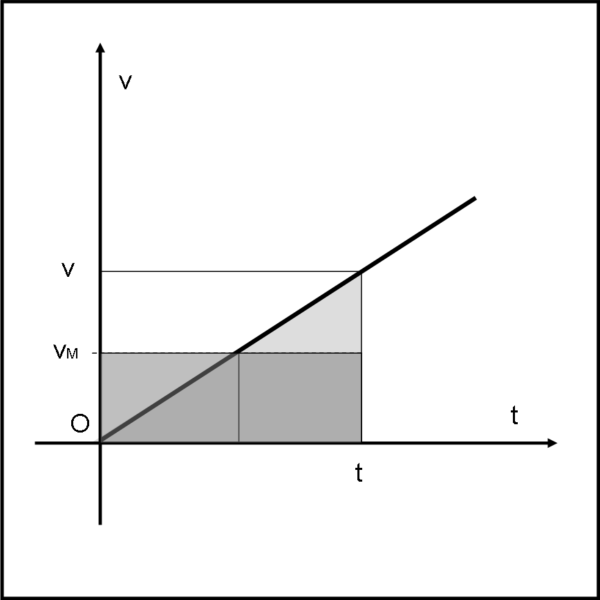
Questa volta non si ottiene certo un rettangolo, ma un triangolo (abbiamo posto v₀ = 0, ossia l’oggetto parte da fermo). Sarebbe molto bello che l’area del triangolo fosse proprio lo spazio percorso… Beh… è proprio così! Basta fare un piccolo ragionamento.

La velocità, rispetto al tempo, descrive una retta. Si può allora considerare senza problemi una velocità media, data proprio da v_M = v/2. Lo spazio percorso nel tempo t con velocità variabile linearmente è uguale allo spazio percorso con una velocità costante uguale a v_M. In parole povere, tutto ciò che abbiamo guadagnato prima di t/2 lo perdiamo dopo t/2 e il risultato è lo stesso. Lo spazio percorso nel tempo t è dato allora da

s = 1/2 vt

Ripetiamo che non abbiamo fatto altro che trasformare un moto uniformemente accelerato in un moto uniforme con velocità uguale al valor medio tra le velocità iniziale e finale. Possiamo allora trasformare il nostro triangolo in un rettangolo che ha un lato uguale a t e un’altezza uguale a v/2.

Ma la sua area è proprio vt/2, ossia esattamente l’area del triangolo di partenza. Abbiamo dimostrato facilmente che anche nel caso di un moto uniformemente accelerato l’area compresa tra la traiettoria della velocità e l’asse delle x è proprio lo spazio s dato da:

s = 1/2 vt       …. (3)

Il nostro moto è però uniformemente accelerato e dobbiamo far comparire l’accelerazione…

Possiamo “recuperare” quanto trovato nella Fig. 4, ossia:

v = at

Sostituendola nella (3) si ha:

s = 1/2 at²       …. (4)

Che è proprio la legge oraria di un corpo che si muove di moto uniformemente accelerato. Lo spazio descrive una parabola in funzione del tempo.

Nel caso che non si partisse dall’origine, ma da un punto di ascissa s = s₀ con una velocità iniziale v₀ (caso più generale possibile), l’equazione precedente diventerebbe la ben nota:

s = s₀ + v₀t + ½ at²   …. (5)

Ecco, quindi, le poche formule fondamentali da conoscere e utilizzare:

s = s₀ + v₀t                                    (A)    legge oraria del moto rettilineo uniforme

s = s₀ + v₀t + 1/2 at²                 (B)    legge oraria del moto uniformemente accelerato

v = v₀ + at                                      (C)    legame velocità - tempo nel moto uniformemente accelerato

che ovviamente si semplificano se si considerano, al tempo t = 0,  v₀ = 0 e s₀ = 0

Vediamo di fare subito un esempio che implichi solo moti rettilinei uniformi. Siamo nel caso più semplice, ma l'esercizio ci permette di risolvere un problema reale con una buona approssimazione.

Un motoscafo in un fiume 

Il luogo del problema è un fiume in cui la velocità della corrente è v_C, costante (Fig. 1).

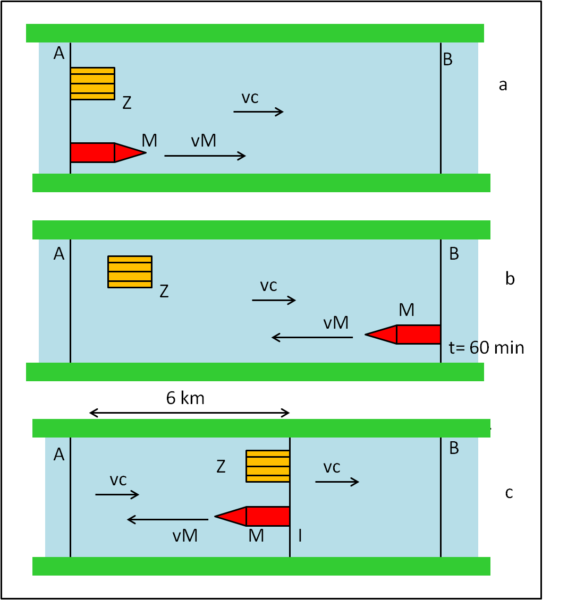
In un certo punto A, un motoscafo M affianca una zattera Z (Fig. 1a). Il motoscafo viaggia a una velocità costante v_M, mentre la zattera Z è spinta solo dalla corrente.

Dopo 60 minuti il motoscafo raggiunge il punto B e decide di tornare indietro, mantenendo sempre la sua velocità v_M. Consideriamo nullo il tempo in cui il motoscafo inverte la rotta (Fig. 2b).

Dopo un certo periodo di tempo il motoscafo incontra nuovamente la zattera Z nel punto I, che dista 6 km dal punto A (Fig. 3c).

Determinare la velocità della corrente v_C.

 

Chi vuole provare a fare da solo può fermarsi qui...

 

Poniamo il tempo t = 0, quando le due imbarcazioni si trovano in A e consideriamole già in movimento.

La zattera Z viaggia solo spinta dalla corrente, per cui la sua velocità è v_C. Il motoscafo, quando si muove verso destra, all'andata, ha una velocità che è la sua v_M più quella della corrente, ossia:

v_Ma= v_M + v_C                     .... (1)

mentre quando torna indietro la sua velocità risulta essere:

v_Mr = v_M - v_C                           ....(2)

In poche parole, all'andata viene spinto dalla corrente, mentre al ritorno il motoscafo deve rallentare, dato che  la corrente si oppone al suo movimento.

Vediamo di scrivere l'equazione del moto per il motoscafo. Come detto è un moto rettilineo uniforme che si svolge in due parti, una in cui la velocità è v_Ma e una in cui la velocità è v_Mr. L'unica formula da utilizzare è la (A), ossia s = so + vt. Possiamo considerare s0 = 0  ( il moto inizia  a partire da punto A) e scrivere

Moto di andata (da A a B):

s_a = AB = v_Ma t_a                      .... (3)

t_a è il tempo necessario a raggiungere B. AB = s_a è lo spazio percorso all'andata.

Moto di ritorno (rispetto a B):

sr = BI = - v_Mr t_r                 .... (4)

s_r è lo spazio percorso dal motoscafo da B fino all'incontro con la zattera e t_r è il tempo trascorso. Abbiamo messo il segno meno allo spazio percorso al ritorno in quanto il motoscafo ha invertito la rotta e si riavvicina al punto A.

Lo spazio finale percorso dal motoscafo (AI), rispetto ad A,  è dato dalla somma di quello di andata e quello di ritorno:

s_f = AI = s_a +  s_r = AB + BI

Possiamo scrivere, dalle (3) e (4):

s_f = v_Ma t_a - v_Mr t_r

Ricordando la (1) e la (2), si ha:

sf= (v_M + v_C)ta - (v_M  - v_C)t_r

Ma noi conosciamo lo spazio finale s_f = AI ed esso vale 6 km.

6 = v_Mt_a + v_C t_a - v_Mt_r + v_C t_r

6 = v_M (t_a - t_r) + v_C (t_a + t_r)

Conosciamo, però, anche t_a che è uguale a 1 ora (60 minuti) e possiamo scrivere:

6 = v_M(1 - t_r) + v_C(1 + t_r)                                .... (5)

Analizziamo, adesso, il moto della zattera. Essa ha viaggiato per 1 ora più t_r a una velocità v_C, percorrendo 6 km. Ossia:

6 = v_C (1 + t_r)                                                         .... (6)

Possiamo uguagliare i secondi membri della (5) e (6) e ottenere:

v_M (1 - t_r) + v_C(1 + t_r) = v_C(1 + t_r)

v_M(1 - t_r) = 0                                 .... (7)

dato che v_M è sicuramente diversa da 0, la (7)  ci dice che

tr = 1 h

Dalla (6) abbiamo,  perciò:

6 = v_C (1 + 1) = 2 v_C

da cui

v_C = 6/2 = 3 km/h

Un esercizio semplice, in quanto utilizza soltanto la formula (A), ma che in qualche modo stimola anche il ragionamento...

Gli esercizi continuano...