(Q) Cade la neve ... ****

10/09/23

(Q) Cade la neve ... ****

Categorie: Fisica classica Tags: Scritto da: Vincenzo Zappalà Commenti:3

Mentre sto continuando a preparare articoli molto divulgativi sulla fisica classica, non potevo fare annoiare i più esperti (qualcuno c'è senz'altro, oltre a Maurizio e Andy...) e quindi ecco un bel quiz "fisico" adatto a loro. Ho messo 4 asterischi non certo per i calcoli da fare, ma solo per  l'impostazione dell'analisi del problema che, comunque, usa il linguaggio della fisica, ossia la matematica, ad un livello decisamente basso. Un problema  schematizzato e non certo molto realistico, che ha, però, una soluzione un po' laboriosa, ma sicuramente divertente.

Che sia data oppure no una soluzione, noi lo descriveremo passo dopo  passo  come un esercizio che è, in pratica, di sola cinematica.

Problema

In un paesino di montagna inizia a nevicare al mattino. La nevicata è molto fitta e l’accumulo di neve cresce a un ritmo costante. A mezzogiorno si mette in azione lo spazzaneve che percorre 2 km la prima ora e 1 km la seconda. Esso mantiene una velocità che è inversamente proporzionale all’altezza della neve accumulatasi.

Si chiede: a che ora ha iniziato a nevicare?

 

Articoli correlati

3 commenti

  1. Fabrizio
    11/09/2023 at 09:16

    Propongo questa soluzione che contiene alcuni passaggi matematici con integrali. Spero di non avere frainteso il quiz.

    Indico con h il tempo trascorso in ore dall'inizio della nevicata.

    La neve accumulata, a, è proporzionale al tempo trascorso, cioè una costante moltiplicata per h: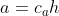 a=c_a h

    La velocità dello spazzaneve è inversamente proporzionale alla neve accumulata, cioè una costante diviso a:

    v_s=\dfrac{c_s}{a}=\dfrac{c_s}{c_ah}=\dfrac{c}{h}   Ho accorpato in un unica costante il rapporto tra le due costanti.

    Lo spazio percorso dallo spazzaneve è la velocità per il tempo. Poiché la velocità è variabile nel tempo, devo usare l'integrale per fare il calcolo. Indico con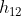 h_{12} il tempo trascorso fino a mezzogiorno.

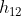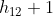    La distanza percorsa dallo spazzaneve tra  h_{12} e h_{12}+1 è 2 volte la distanza percorsa dallo spazzaneve tra  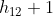h_{12}+1 e h_{12}+2.

    \int_{h_{12}}^{h_{12}+1}\dfrac{c}{h}dh=2\int_{h_{12}+1}^{h_{12}+2}\dfrac{c}{h}dh.    La costante c appare a destra e sinistra e può essere eliminata.

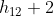    Poiché l'integrale di 1/h è ln(h), avrò che

    \ln({h_{12}+1})-\ln({h_{12}})=2[\ln({h_{12}+2})-\ln({h_{12}+1})]

    La differenza tra logaritmi è il logaritmo del rapporto tra gli argomenti. La moltiplicazione di un logaritmo è il logaritmo della potenza dell'argomento. Avrò quindi che:

    \dfrac{{h_{12}+1}}{{h_{12}}}=\dfrac{({h_{12}+2})^2}{{(h_{12}+1)^2}}   da cui l'equazione  (h_{12}+1)^3=h_{12}(h_{12}+2)^2

    Fortunatamente i termini di 3° grado si semplificano è ho una equazione di secondo grado:

    h_{12}^2+h_{12}-1=0  che ha come soluzione positiva h_{12}=\frac{\sqrt{5}}{2}-\frac{1}{2}.

    Quindi deve avere iniziato a nevicare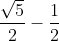 \frac{\sqrt{5}}{2}-\frac{1}{2} ore prima di mezzogiorno.

     

  2. Vincenzo Zappalà
    11/09/2023 at 09:47

    che piacere risentire Fabry (che ci sta anche preparando un bel regalo) :-P ! Lascio ancora il quiz aperto per vedere se si muovono anche altri "esperti"

  3. Maurizio Bernardi
    11/09/2023 at 11:30

    Ottimo, condivido impostazione e calcolo. Bravo Fabrizio .

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.