Il problema che andiamo a risolvere riguarda uno dei tanti che sono stati inseriti nell'esame per l'ingresso all’istituto indiano di tecnologia. L'ho scelto, in quanto riguarda un argomento astrofisico, ma i problemi proposti spaziano dalla fisica, alla chimica e alla matematica. L'esame è considerato uno dei più difficili al mondo. Tuttavia, il problema del nostro articolo non è di per sé molto difficile e ben si adatta alle capacità medie del nostro Circolo. Ciò che rende unico l'esame, in generale, è il grande numero di problemi da risolvere. Per riuscire a ottenere un punteggio adeguato non restano che un paio di minuti per ogni esercizio. In pratica, esperienza, conoscenza ed estrema rapidità!

Riporto pari pari il testo dell'esercizio. La soluzione che ci si aspetta è numerica, in modo che sia facile un controllo sull'esattezza del risultato:

Due stelle sferiche A e B hanno densità ρ_A e ρ_B, rispettivamente. A e B hanno lo stesso raggio, mentre la massa di B (M_B) è due volte quella di A (M_A). A causa di un processo di interazione, la stella A perde parte della sua massa e il suo raggio si dimezza, mantenendo comunque la forma sferica e la stessa densità. L'intera massa persa da A si va ad accumulare sulla stella B sotto forma di uno spesso guscio sferico. Questo guscio continua ad avere densità ρ_A. Se v_A e v_B sono le velocità di fuga  dopo l'interazione, il loro rapporto risulta essere: v_B/v_A = √(1o n/15^1/3). Il valore di n è .......

Non solo soluzione, quindi, ma anche secondo il giusto metodo...

Bene, chi vuole provare da solo è invitato a farlo, guardando il tempo impiegato. Noi descriveremo un metodo che ci porta proprio al valore richiesto di n.

Il problema può essere riassunto attraverso la Fig. 1

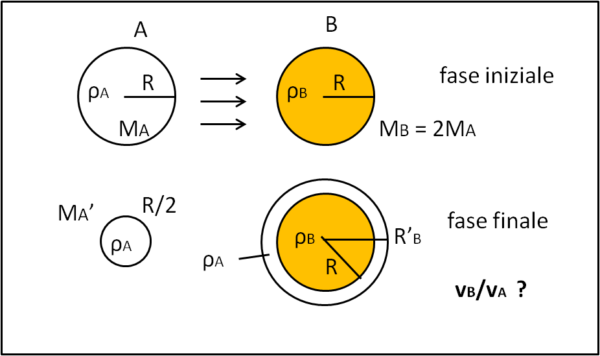
Analizziamo ciò che è conosciuto e ciò che dobbiamo trovare. Ovviamente, dobbiamo ricordare quanto vale la velocità di fuga.

v = √(2GM/R)

Nel nostro caso:

v_A = √(2GM_A'/R_A') = √(2GM_A'/(R/2)) = √(4GM_A'/R)                 .... (1)

v_B = √(2GM_B'/R_B')                                                                                .... (2)

Le grandezze necessarie per i calcolo sono la massa di A dopo l'interazione (M_A' ),il raggio della stella B dopo il ... "pasto" (R_B') e la sua massa M_B' .

Iniziamo da M_A'.

Essa è la massa di A, in funzione di MA, che rimane dopo il trasferimento di una sua parte su B.

Ci viene in aiuto la densità che rimane costante, ossia il rapporto tra le masse, dopo e prima del trasferimento, e i volumi rispettivi:

ρ_A = M_A/Vol_A = M_A'/Vol'_A

M_A' = M_A Vol'A/Vol_A = M_A R'³/R³ = M_AR³/(8 R³) = M_A/8

che inserita nella (1) ci regala il valore di v_A

v_A = √(4GM_A/(8R))

vA = √(GM_A/(2R)) 

Passiamo, ora, al calcolo di M_B'.

Il calcolo è facilissimo, dovendo solo aggiungere a M_B = 2M_A la massa ricevuta dalla stella A. Abbiamo visto che la massa rimanente è solo 1/8 della massa iniziale, il che ci porta a dire che la massa trasferita è 7/8 di M_A. Basta fare una somma:

M_B' = M_B + 7/8 M_A = 2M_A + 7/8 M_A

M_B' = (23/8)M_A

Ci resta da calcolare R_B' in modo da completare il calcolo di v_B.

Il modo migliore di agire è quello di calcolare il volume totale di B dopo il trasferimento di massa. Per far ciò dobbiamo calcolare il volume della massa proveniente da A (poco importa come si sistemi su B).

La densità di questa massa trasferita rimane costante per cui:

ρA = (7M_A/8)/Vol_A' = M_A/Vol_A

da cui

Vol_A' = 7/8 Vol_A

Risultato ovvio dato che 7/8 è anche il rapporto delle masse e quindi quello dei volumi essendo costante la densità.

VolB' = VolB + 7/8 VolA

Sia a sinistra che a destra abbiamo dei volumi di sfere, per cui

la stessa relazione vale per i raggi al cubo (volume della sfera = 4/3π R³)

R_B³ = R³ + 7/8 R³

R_B³  = 15/8 R³

R_B = 15^1/3 R/2

Inseriamo le due grandezze appena trovate (M_B' e R_B) nella (2)

v_B = √(2GM_B'/R_B) = √(2G(23/8)M_A/(15^1/3R/2)) = √(4G(23/8)M_A/(15^1/3R)) = √(G(23/2)M_A/(15^1/3R))

v_B = √(G(23M_A/(2 (15^1/3R)))

Non ci resta che fare il rapporto tra v_B e v_A

vB/vA = √(G(23M_A/(2 (15^1/3R)) · (2R/(GM_A)) = √(G 23M_A 2 R/(2 15^1/3RGM_A))

vB/vA = √(23/15^1/3)

Il risultato è, quindi:

n = 2.3

Ho sicuramente scritto dei passaggi che potevano anche essere evitati, per cercare di essere il più semplice possibile, ma, benché il procedimento sia alla portata di chiunque devo ammettere che due minuti è veramente un tempo "record", anche se sappiamo quanto siano bravi gli indiani nella matematica.

Magari, in seguito, proporremo qualche altro test di questo genere...