Categorie: Fisica classica
Tags: cinematica legge di Torricelli moto uniformemente accelerato
Scritto da: Vincenzo Zappalà
Commenti:0
(CIN) Equazione di Torricelli *
Questo articolo è inserito in Cinematica
Può capitare, nel moto uniformemente accelerato, che non vi sia bisogno del tempo e quindi si voglia legare direttamente la velocità con l'accelerazione, conoscendo lo spazio percorso.
Ricordiamo le due formule fondamentali
s = s0 + v0 t + 1/2a t2
v = v0 + at
Dalla seconda ricaviamo
t = (v - v0)/a
Andiamo a inserirlo nella prima formula
s = s0 + v0(v - v0)/a + 1/2 a (v - v0)2/a2
s = s0 +(v0v - v02)/a + 1/2(v2 + v02 - 2vv0)/a
2as = 2s0a + 2v0v - 2v02 + v2 + v02 -2vv0
2as = 2s0a + v2 - v02
v2 = 2a(s - s0) + v02 .... (1)
Essa, in pratica, ci permette di determinare la velocità finale conoscendo accelerazione e spazio percorso.
Se la posizione iniziale è posta uguale a zero e tale è anche la velocità iniziale, la formula si riduce a:
v2 = 2as .... (2)
Facciamo subito un esempio risolvendo un facile esercizio.
Una pistola spara un proiettile contro a un muro. Il proiettile tocca il muro con una certa velocità v0 e penetra per uno spazio s. Qual è l'accelerazione del proiettile all'interno del muro?
Consideriamo la (1)
la velocità finale è zero , dato che il proiettile si ferma. La velocità iniziale è v0. Consideriamo come origine s0 il punto in cui il proiettile tocca il muro:
0 = 2as +v02
2as = -v02
a = -v02/2s
Ovviamente l'accelerazione è negativa in quanto il proiettile viene decelerato.
Questa formula è stata introdotta da Evangelista Torricelli e la ben nota legge di Torricelli è un caso particolare di questa formula.
La legge dice che
la velocità di un fluido in uscita da un foro (di sezione molto piccola rispetto alle dimensioni del recipiente) è pari alla radice quadrata del doppio prodotto dell'accelerazione di gravità e della distanza "h" fra il pelo libero del fluido e il centro del foro che è stato praticato:
v = √(2gh)
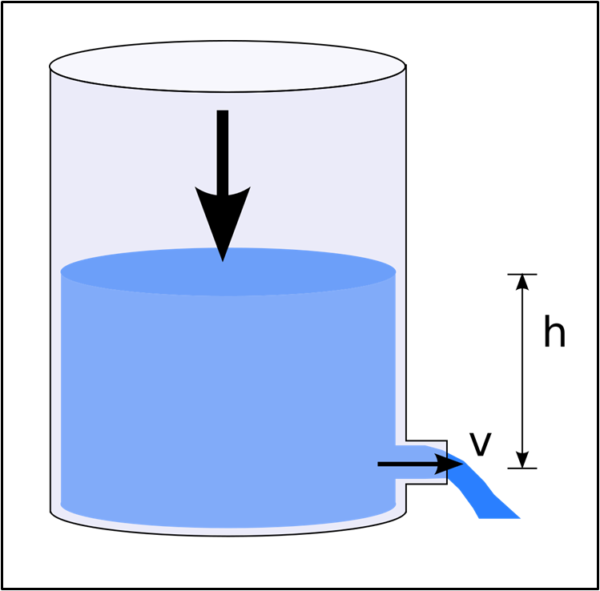
La velocità iniziale è uguale a zero così come lo è la posizione dell'acqua in superficie.
Applichiamo la (1) ponendo v0 = 0, ricordando che l'accelerazione non è altro che quella di gravità e che h è l'altezza dell'acqua, ossia lo spazio percorso dal fluido prima di entrare nel foro.
v2 = 2g(s - 0)
v = √(2gh)
La prossima volta inizieremo con qualche esercizio di cinematica a due dimensioni (quella lineare è decisamente troppo facile...).





