(QI) Come semplificare un'espressione "diabolica" ****
Mentre i comuni mortali sono alle prese con la cinematica e i momenti d'inerzia, ecco, per i più esperti (che, altrimenti, si girerebbero i pollici)una bella espressione da risolvere...
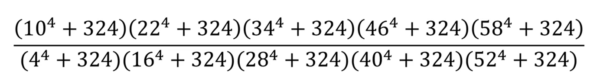
Ovviamente è proibito eseguire tutti i calcoli utilizzando il computer o calcolatrici in genere. Nessuno pretende, inoltre, che si effettuino a mano tutti i calcoli (poveri noi!).
La soluzione è molto meno impegnativa, come "lavoro bruto", ma bisogna eseguire qualche "semplice" passaggio algebrico e ridurre il tutto al calcolo di due semplici moltiplicazioni, un paio di somme e una divisione.
Si chiede, perciò, il risultato dell'espressione (con tutti i passaggi eseguiti).
Per aiutarvi un pochino, posso dire che Daniela sarà molto contenta di questo quiz e che , in fondo in fondo, il quiz ha a che fare con l'Astronomia.
QUI la soluzione
6 commenti
I fattori a denominatore e numeratore hanno una struttura comune.
)
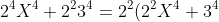Posso scriverli in questo modo
Elenco questi X chiamando A quelli a numeratore e B quelli a denominatore.
A: 5 11 17 23 29
B: 2 8 14 20 26
Da notare che alternando le due righe gli elementi consecutivi differiscono di 3.
Da notare anche che i fattori 2 al quadrato sono nello stesso numero a numeratore e denominatore, quindi si elidono.
Ciascuno dei termini rimanenti si può espandere in due fattori in questo modo:
=2^2X^4+3^4+2~&space;2&space;X^2&space;3^2-2&space;~2&space;X^2&space;3^2)
i primi 3 addendi sono un quadrato
=(2X^2+3^2)^2-2~&space;2&space;X^2&space;3^2)
applico la regola della differenza tra quadrati
=(2X^2+3^2-2X3)(2X^2+3^2+2X3))
aggiungo e sottraggo una stessa quantità
questi sono 2 fattori
Confronto i fattori che trovo a numeratore e denominatore
(2A^2+3^2+2A3))
(2B^2+3^2+2B3))
per identificarli li chiamo nell'ordine A-, A+, B- e B+.
Si elidono gli eventuali fattori uguali a numeratore e denominatore
Ovviamente sono uguali se A=B, ma non ce ne sono.
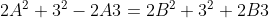
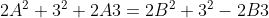
Possono essere uguali anche incrociando i termini:
o
Sviluppo la prima uguaglianza:
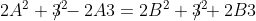
=2B(B+3))
Le soluzioni son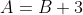o:
o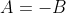 
(questa non ci serve poiché B sono positivi e non abbiamo A negativi)
Se vale questa condizione i fattori A- B+ si elidono.
In modo simile ricavo che se
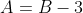i fattori in A+ e B- si elidono.
Esamino la lista B e verifico se B+3 e B-3 sono nella lista A: 5 11 17 23 29
B: 2 8 14 20 26
A=B+3 5 11 17 23 29 si elidono tutti gli A- e B+. Qualsiasi sia B, B+3 è sempre in A
A=B-3 no 5 11 17 23 si elidono tutti gli A+ e B- ad eccezione di 29+ e 2-.
Non c’è nessun B-3=29 e B-3=2-3=-1 non è in A.
Quindi ne rimangono 1 a numeratore (29+) ed 1 a denominatore (2-)
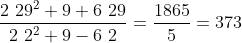Qui ho usato la calcolatrice.
Volendola fare senza calcolatrice conviene scriverla così:
La mia soluzione è leggermente più lunga, ma tutti i calcoli possono essere effettuati anche a mente.
Bravissimi i due "cavalieri" matematici Fabry e Andy!!! La soluzione di Andy sembra più lunga, ma poteva anche essere contratta ricordando proprio il prodotto telescopico. Quindi... perfetta così come quella più articolata di Fabry. E' un vero piacere ragionare... grazie!
Pubblicherò quanto prima la soluzione spiegando bene la nascita di un prodotto notevole, ben poco conosciuto.
Intanto, la nostra Dany potrebbe cominciare ad avvicinarsi a una grande matematica, che ha subito le solite angherie maschiliste: Marie-Sophie Germain. Troverà pane per i suoi denti e forse l'ispirazione per farcela conoscere meglio!
Gran bel personaggio questa Marie-Sophie Germain! Basti pensare che ha trovato il modo per farsi beffe del sistema pur di realizzare il sogno di studiare matematica, conquistandosi la stima di nientepopodimeno che Lagrange e Gauss.
Meriterebbe sicuramente un giro di applausi anche nel nostro Teatro, vediamo cosa si può fare...
ero sicuro del tuo (e nostro) interesse! Viva le donne
e qui mi associo