Diamo la soluzione dell'espressione "diabolica", ricordando la grande matematica Sophie Germain.

Notiamo che ogni parentesi è della forma:

x⁴ + 324

Ma 324 è divisibile per 4  dando risultato 81 che è, ovviamente, uguale a 3⁴. Per cui possiamo scrivere.

x⁴ + 324 = x⁴ + 4(3⁴)

A questo punto dobbiamo ricordarci  (o imparare) un'identità poco conosciuta, ma di grande utilità, dovuta a una grande matematica, Marie Sophie Germain:

a⁴ + 4b⁴ = (a² + 2b² - 2ab)(a² + 2b² + 2ab)

Provare per credere ...

Possiamo applicare l'identità al nostro caso e ottenere:

x⁴ + 4(3⁴) = (x² + 2 · 3² - 2· 3x)(x² + 2 · 3² - 2 · 3x) = (x² +18 - 6x)(x² +18 + 6x) = (x(x - 6) + 18)(x(x + 6) + 18)

Applichiamo il risultato alla prima parentesi del numeratore della nostra espressione:

(10⁴ + 324) = (10(10 - 6) + 18)(10(10 + 6) + 18) = (10(4) + 18)(10(16) + 18)

e alla prima parentesi al denominatore:

(4⁴ + 324) = (4(-2) + 18)(4(10) + 18)

Effettuiamo il rapporto tra di loro:

(10⁴ + 324)/(4⁴ + 324) = (10(4) + 18)(10(16) + 18)/(4(-2) + 18)(4(10) + 18)

Dobbiamo eseguire questo calcolo? Assolutamente no, dato che possiamo eseguire una notevole semplificazione: i termini colorati in rosso si elidono! Per cui:

(10⁴ + 324)/(4⁴ + 324) = (10(16) + 18)/(4(-2) + 18)

Non è certo difficile continuare a scrivere gli altri rapporti e, facendolo, ci troviamo di fronte a qualcosa di "magico":

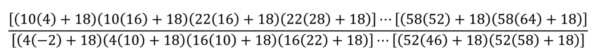
Non vi è bisogno di fare calcoli, dato che le parentesi al numeratore si eliminano con quelle al denominatore. Rimane solo la prima al denominatore e l'ultima al numeratore:

(58(64) + 18)/(4(-2) + 18)

Ci siamo imbattuti in un prodotto telescopico, come dice bene Andy! Perché si chiama telescopico? Basta guardare la figura che segue e che mostra un telescopio retrattile: ciò che appare molto lungo può ridursi a qualcosa di estremamente maneggevole...

Basta, perciò eseguire le semplici operazioni a cui l'espressione si è ridotta per ottenere il risultato finale che vale

373