Come indicato da Andy, la soluzione del quiz è veramente semplice. Infatti, non vi è nessun bisogno di calcolare le aree colorate, ma solo di quelle colorate a cui si è aggiunta una stessa area. Il tutto, quindi, si risolve considerando l'area di un quarto di cerchio e quella di metà cerchio. Vediamo la figura che segue e che illustra il piccolo "trucco".

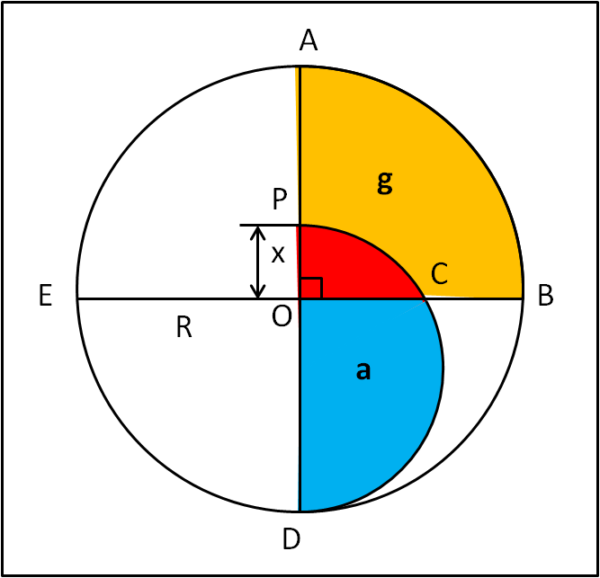
Aggiungiamo alle due aree colorate l'area colorata in rosso. Non ci resta che confrontare queste due nuove aree di facile determinazione. La loro uguaglianza implica anche l'uguaglianza delle due aree originali.

Area azzurra + area rossa = Area gialla + area rossa

semicerchio di raggio (R + x)/2   = quarto di cerchio di raggio R

(1/2)π (R + x)²/4 = 1/4 π R²

1/2(R² + x² + 2Rx) = R²

R² + x² + 2Rx = 2R²

x² + 2Rx - R² = 0

x = - R +/-√(R² + R²)

x = - R +/- R√2

Prendiamo ovviamente il valore positivo

x = R(√2 - 1)

Scusate... ma mi sorprendo sempre di più vedendo la difficoltà che esiste nell'affrontare questi semplici problemini.