Questa volta voglio modificare leggermente la strategia, per cercare di avvicinare anche i lettori meno esperti  a problemi geometrici di notevole complessità. In poche parole, descriverò la soluzione senza trascurare alcun passaggio, in modo da potergli assegnare due soli asterischi. Chiunque sarà, perciò, in grado di seguire la trattazione, facendo molta attenzione a ogni conclusione parziale e con la dovuta pazienza. Si impareranno e/o torneranno in mente molte proprietà interessanti del triangolo e del cerchio... Non ve ne pentirete!

La prima cosa da fare è, come al solito, capire esattamente cosa è necessario provare per dimostrare la tesi.

Angoli alla circonferenza

Consideriamo la nostra La nostra Fig. 1 di partenza

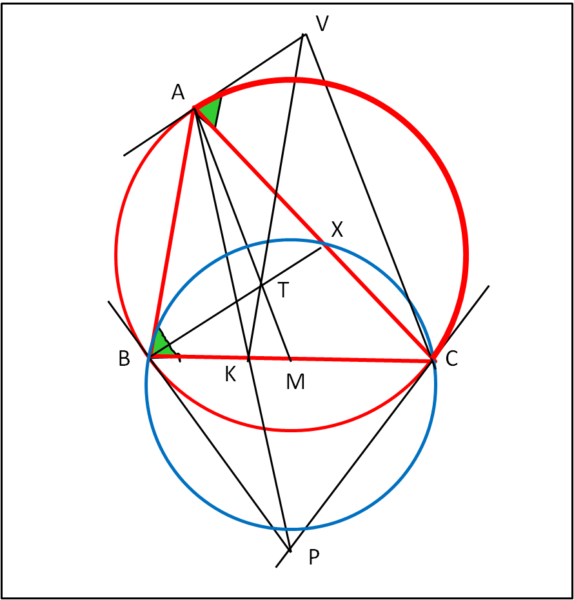
Dobbiamo dimostrare la tangenza di AV alla circonferenza rossa, La prima cosa che potrebbe venire in testa sarebbe di dimostrare che AV è perpendicolare al raggio che dal centro della circonferenza arriva al punto A. Purtroppo, non abbiamo indicato il centro come un dato del problema e non è certo il caso di complicare ancora di più la figura. Vediamo di trovare se esiste una relazione alternativa che dimostri la tangenza di AV.

Consideriamo l’arco di cerchio rosso AC più spesso e indichiamo in verde l’angolo alla circonferenza CBA. Sappiamo bene che tutti gli angoli alla circonferenza di uno stesso arco sono uguali. In particolare, nelle condizioni limite in cui il punto “variabile” sulla circonferenza coincida con uno degli estremi dell’arco, l’angolo alla circonferenza diventa l’angolo tra la tangente alla circonferenza e la congiungente i due estremi dell’arco. Mostriamo, ancora un volta, in Fig. 2, quanto abbiamo appenda detto a parole…

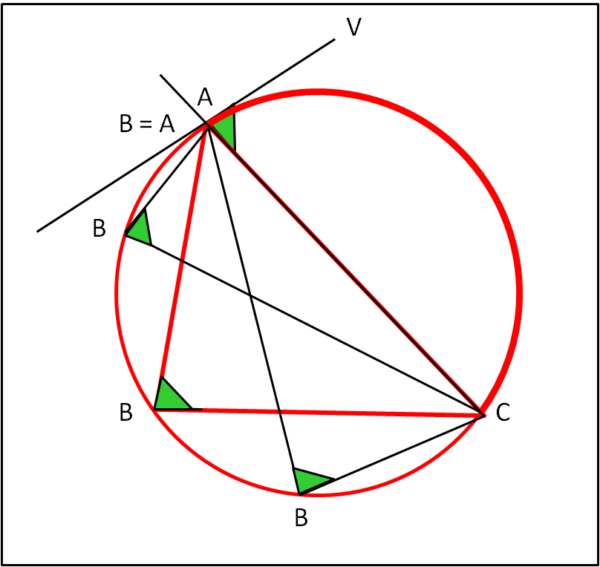
B è il punto sulla circonferenza che variando lungo di essa comporta sempre uno stesso angolo ABC. Quando B va a coincidere con A , l’angolo alla circonferenza è proprio quello tra la tangente in A e la congiungente AB.

Ne segue, quindi, che se dimostrassimo l’uguaglianza di CAV e CBA, dimostreremmo che la retta AV è proprio tangente alla circonferenza in A.

Triangoli simili

Riflettiamo un po’ sulla Fig. 1 e sugli angoli verdi che sembrano il punto chiave dell’intera faccenda. Riportiamola in Fig. 3.

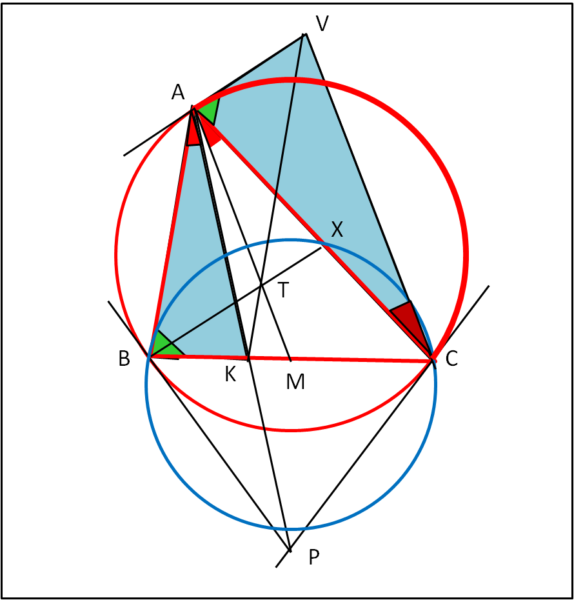
In particolare, osserviamo che gli angoli verdi appartengono ai due triangoli azzurri AVC e ABK. Triangoli che sembrerebbero essere simili tra loro… Possiamo cercare di provarlo? E perché no!?

Innanzitutto, analizziamo gli angoli segnati in rosso BAK e ACV. Che bello se fossero uguali! Non possiamo ancora provarlo, ma possiamo sfruttare il fatto che VC sia stata costruita come parallela ad AM. Questo parallelismo  implica immediatamente che l’angolo ACV sia uguale all’angolo  MAC (alterni interni di rette parallele tagliate da una trasversale).

Ne segue che se mostrassimo che MAC è uguale a BAK dimostreremmo anche che BAK è uguale ad ACV. Sarebbe un bel colpo verso la similitudine dei triangoli azzurri.

I più esperti, a questo punto, potrebbero sorridere, dato che esiste un teorema che stabilisce proprio quanto vorremmo dimostrare. Noi, però, facciamo finta di non conoscerlo e cerchiamo di dimostrarlo, ossia di dimostrare che MAC è uguale a BAK.

Un teorema poco conosciuto

Andiamo a considerare la Fig. 1 iniziale sotto un aspetto diverso e riproponiamola in Fig. 4.

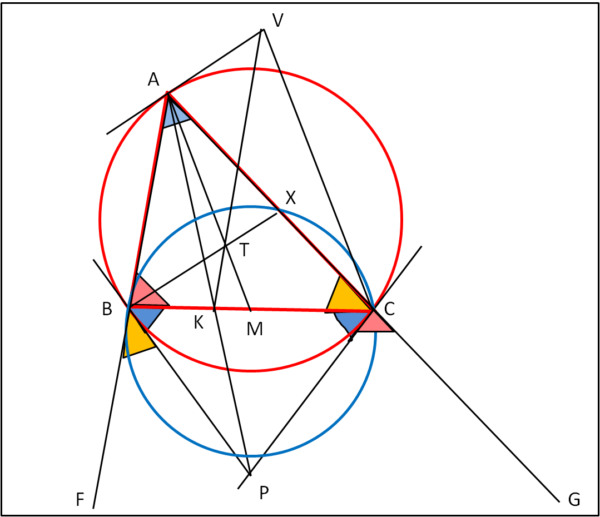
Per quanto dimostrato con la Fig. 2, relativamente agli angoli alla circonferenza, possiamo dire che l’angolo azzurro BAC è uguale all’angolo azzurro PBC, entrambi relativi all’arco BC (PB è tangente per costruzione).

BAC = PBC                              …. (1)

Torniamo al triangolo ABC.

La somma degli angoli interni di un triangolo è 180°. Abbiamo, perciò, che:

ACB  = 180 – ABC – BAC

Prolunghiamo il lato AB fino a un punto F a piacere. AF è una retta per costruzione. Ne segue che:

FBP = 180 – ABC – PBC

Ma, abbiamo appena visto (1) che:

BAC = PBC

Per cui:

ACB = FBP                            … (2)

In modo del tutto analogo, possiamo dire che BAC e PCB sono angoli alla circonferenza dell’arco BC e quindi:

BAC = BCP                …. (3)

Inoltre  è  ovvio che:

ABC  = 180 – ACB – BAC

Prolunghiamo il lato AC fino a G.

Abbiamo che:

PCG = 180 – ACB – BCP

Ma abbiamo appena dimostrato (3) che

BAC = BCP

Per cui:

ABC = PCG                     …. (4)

Fermiamoci un attimo a ragionare …

Le relazioni appena trovate ci permettono di ribadire alcune interessanti conclusioni che sono evidenziate dai colori dei vari angoli. In particolare abbiamo anche trovato che gli angoli azzurri sono uguali tra loro, ossia:

PBC = BCP

Ne segue che il triangolo PBC è isoscele e, quindi:

PB = PC

Diventa, allora, più che ragionevole pensare a una circonferenza di centro P e raggio PB = PC. Detto fatto nella Fig. 5

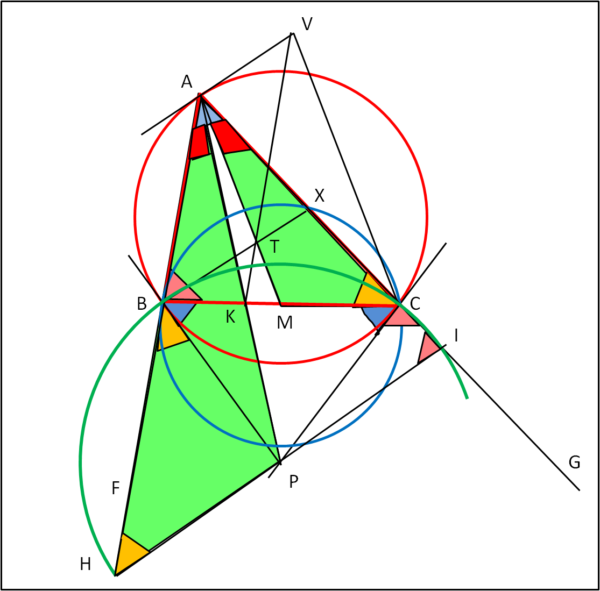
Tracciata la circonferenza verde non ci resta che considerare le due intersezioni di questa circonferenza con le rette AF e AG, indicandole con H e I.

PH e PB sono raggi della circonferenza per cui il triangolo HBP è isoscele, ossia:

HBP = PHB

Non possiamo dimenticare, però, che per la (2) vale anche:

ACB = FBP = HBP

Per cui:

PHB = ACB

In modo del tutto simile possiamo concludere che:

CIP = ABC

I colori assegnati agli angoli ci fanno vedere molto bene la situazione.

Facciamo ora molta attenzione alle apparenze... Dalla figura sembrerebbe ovvio dire che AHI è un triangolo. Ma così non è, dato che noi abbiamo tracciato i segmenti PH e PI separatamente, unendo il centro P con due punti della circonferenza e NON abbiamo tracciato un unico segmento HI che passi per P. Teoricamente AHPI potrebbe essere un quadrilatero.

Se così fosse, però, la somma dei suoi angoli dovrebbe essere 360°.

Sommiamo gli angoli del supposto “quadrilatero”:

BHP + HPI + PIC + BAC = 360°                        …. (5)

Tuttavia, abbiamo appena dimostrato che

BHP = ACB

e che

PIC = ABC

Per  cui la (5) diventa:

ACB + HPI + BAC + BAC = 360°             …. (6)

Sappiamo però che, in quanto angoli interni del triangolo ABC, deve valere la relazione:

ABC + ACB + BAC = 180

Sostituendo nella (6) si ha:

180 + HPI = 360

HPI = 180°

Ne segue che H, P e I devono stare su una stessa retta e il supposto “quadrilatero” diventa un semplice triangolo.

Essendo AHI un triangolo possiamo sfruttare l’uguaglianza degli angoli per dire che ABC è simile ad AHI

Ancora un piccolo sforzo…

I dati di partenza ci dicono che M è il punto medio di MC. Sappiamo, però, che anche P è il punto medio di HI, dato che HI è sicuramente un diametro del cerchio verde. La similitudine di ABC e HAI ci permette di dire che:

AH/AC = BC/HI

Dividiamo sia BC che HI per 2 e la proporzione rimane valida

AH/AC = (BC/2)/(HI/2)

Ma la metà di BC è MC, mentre la metà di HI è HP. Per cui:

AH/AC = MC/HP

Sappiamo inoltre che

AHP = ACM

Per il secondo criterio di similitudine (due lati proporzionali e l’angolo compreso uguale), i due triangoli azzurri ACM e APH devono essere simili.

Ne segue che

HAP = MAC

Abbiamo raggiunto un punto importante del problema, ma la strada è ancora lunga, per cui preferisco fermarmi qui e rimandare la seconda parte, in modo che possiate digerire per bene quanto appena scritto.

Ovviamente, questa prima parte potrebbe servire come trampolino di lancio per chi volesse arrivare alla fine da solo. Sarà difficile, ma lasciatemi sperare...

continua …