Per la sfera non abbiamo problemi a scegliere l'asse di rotazione: basta che sia un diametro e passi, perciò, per il centro di massa. Utilizziamo la Fig. 1.

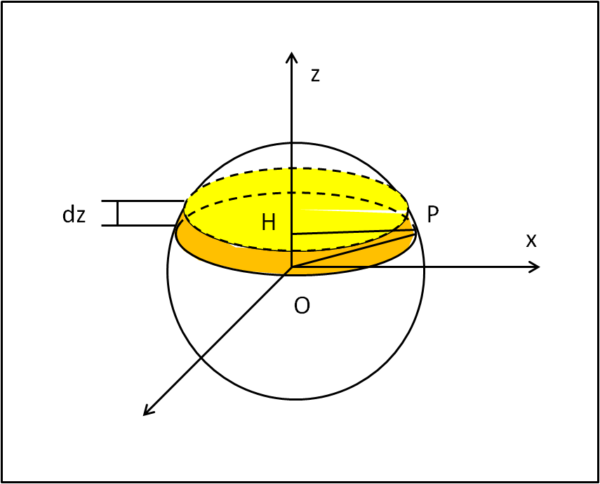
Iniziamo da una sfera piena e definiamo la sua densità:

ρ = M/(4/3 πR³)                              .... (1)

L'asse di rotazione sia z. Tagliamo una "fettina" sottile di sfera (gialla) il cui spessore sia dz. Possiamo considerare il volume di questa fettina pari a quella di un cilindro pieno di altezza dz. Il suo volume è dato da:

dV = πHP²dz                                       .... (2)

la massa dm della fettina è data, ovviamente, da:

dm = ρ dV                                            .... (3)

Il momento d'inerzia della fettina non è altro che il momento d'inerzia di un cilindro pieno di altezza dz che ha come raggio di base HP, ossia:

dI = 1/2 dm HP²

Applichiamo il teorema di Pitagora al triangolo OHP e si ha:

HP² = R² - z²

Con qualche sostituzione (dV dalla (2) e dm dalla (3)), il momento d'inerzia dI diventa

dI = 1/2 πρ(R² - z²)dz (R² - z²) = 1/2πρ(R² - z²)² dz

Sviluppiamo il quadrato

dI = 1/2 πρ (R⁴ - 2R²z² + z² )dz

Non ci resta che integrare tra z = 0 e z = R per ottenere il momento d'inerzia di metà della sfera. Per il momento d'inerzia di tutta la sfera basta moltiplicare per 2:

I = πρ∫₀^R (R⁴ - 2R²z² + z⁴)dz = πρ(∫₀^R R⁴ dz -∫₀^R 2R²z² dz + ∫₀^R z⁴ dz)

L'unica variabile è z, per cui gli integrali sono elementari e abbiamo:

I = πρ([R⁴ z]₀^R  - [2R²(z³/3)]₀^R  + [z⁵/5 ]₀^R)

I = πρ (R⁴R - 2R²R³/3 + R⁵/5) = πρ R⁵( 1 - 2/3 + 1/5) = πρ R⁵(15 -10 +3)/15 = (8/15) πρ R⁵

Inserendo il valore della densità, dato dalla (1)

I = (8/15)π MR⁵ /((4/3) πR³) = MR²(8/15)(3/4)

I = 2/5 M R²

 

Passiamo ora al momento d'inerzia di un guscio sferico, utilizzando la Fig. 2

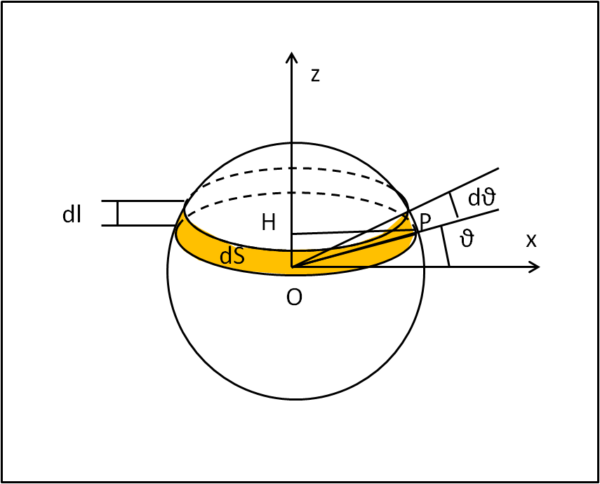
Questa volta consideriamo una sezione dS del guscio la cui altezza è data da dl. Possiamo ovviamente scrivere che

dl = R dθ                                    .... (1)

L'area dS può essere scritta come se fosse quella di una superficie cilindrica che disti HP dall'asse di rotazione e che abbia altezza dl:

dS = 2π HP dl

Introduciamo, come sempre, la densità del guscio sferico (densità di superficie) che è pari al rapporto tra massa totale M e la superficie sferica (4πR²)

ρ = M/4πR²

Nel caso della nostra fettina di guscio sferico, abbiamo:

dm= ρ dS = ρ 2πHP dl = M 2π HP dl/(4πR²) = M HP dl/(2R²)

Ma HP può essere scritto come

HP = R cosθ

per cui:

dm = M R cos θ dl/(2R²)

dalla (1)

dm = M R cos θ R dθ /(2R²)                                               .... (2)

Possiamo perciò scrivere il momento d'inerzia dell'anello sottile cilindrico di massa dm come:

dI = dm HP²

dI = dm(Rcosθ)² = M R cosθ R dθ (R cosθ)² /(2R²) = M R²cos³θ dθ/2

Il momento d'inerzia appena scritto ha come variabile soltanto l'angolo θ, per cui, per ottenere quello dell'intero guscio sferico, basta integrare tra 0 e π/2 e poi moltiplicare per 2, dato che integrando tra 0 e π/2 si ottiene il momento di mezzo guscio sferico

I = 2 MR²∫₀^π/2 cos³θ dθ/2 = MR²∫₀^π/2 cos³θ dθ

Per risolvere l'integrale, scriviamo la ben nota relazione:

cos²θ = 1 - sin²θ

e la usiamo al posto del quadrato del coseno all'interno dell'integrale

I = MR²∫₀^π/2 cos²θ cos θ dθ  = MR²∫₀^π/2 (1 - sin²θ)cos θ dθ

I = MR²(∫₀^π/2 cosθ dθ - ∫₀^π/2 sin²θ cos θ dθ)

Moltiplichiamo e dividiamo per 3 il secondo integrale

I = MR²(∫₀^π/2 cosθ dθ - (3/3)∫₀^π/2 sin²θ cos θ dθ)

notiamo che la derivata di sin³θ  vale 3 sin²θ cosθ, mentre quella di sin(θ) è proprio cos(θ). In definitiva possiamo scrivere:

I = MR² ([sin θ]₀^π/2 - [sin³θ/3]₀^π/2)

I = MR² (1 - 1/3)

I = 2/3 MR²