Questo articolo è inserito in Dinamica

 

Stiamo ancora esercitandoci con vari problemi di cinematica, ma, nel frattempo, il nostro amico Michele ha chiesto di non dimenticarci dell'accelerazione centripeta e centrifuga che, a suo dire (e probabilmente ha ragione) rappresentano ancora un problema per molti.

Senza introdurre forze vere e/o apparenti, spieghiamo in modo "cinematico" estremamente semplice la differenza fondamentale tra le due accelerazioni. Utilizzeremo una "breve" avventura spaziale di un ricchissimo magnate del XXI secolo o giù di lì.

Prima di cominciare, ricordiamoci bene cosa ci hanno insegnato Giordano Bruno e Galileo Galilei: "Se ci muoviamo di moto rettilineo uniforme, nessuno è in grado di stabilire se ci muoviamo noi o tutto ciò che ci sta attorno". In poche parole, dobbiamo ricordarci la relatività di Galileo e il primo principio della dinamica da Newton: un corpo che si muove di moto rettilineo uniforme continua a muoversi nello stesso modo se niente lo viene a disturbare.

Diventa perciò obbligatorio capire bene il significato di sistema di riferimento. Se si sceglie quello del viaggiatore, lui si sente fermo e afferma che è tutto ciò che gli sta attorno che si muove. Se si assume quello di un osservatore esterno, lui dice che è il viaggiatore che si muove, mentre lui sta fermo.

Questi sono concetti che devono essere patrimonio di tutti, altrimenti diventa inutile proseguire nelle spiegazioni, per semplici che siano...

E veniamo alla nostra avventura spaziale.

Un ricchissimo magnate decide di compiere un viaggio spaziale su un'astronave, governata solo dall'Intelligenza Artificiale. Il magnate M non si fida di piloti e personaggi simili, dato che vede in tutti solo potenziali pericoli per le sue ricchezze (in)degnamente acquisite.

L'astronave viene costruita secondo i suoi gusti e, in particolare, con un ampio finestrone F che gli permetta una vista meravigliosa e una porta U di facile apertura da cui possa uscire per immergersi nello spazio profondo: vedrà la Terra sotto di lui e si sentirà veramente il padrone del mondo. Gli hanno detto che la partenza è un momento abbastanza fastidioso a causa di accelerazione o qualcosa del genere e quindi si fa dare un sonnifero di breve durata per svegliarsi quando ormai l'astronave avrà raggiunto la velocità di crociera.

Tutto fila perfettamente liscio ed è ormai nelle sicure mani dell'IA, la quale, ovviamente, segue le direttive che le sono state impartite direttamente dal magnate. Il magnate guarda il finestrone e rimane un po' dubbioso... Lui si sente perfettamente fermo, mentre è la Terra che sta viaggiando a velocità sostenuta, allontanandosi sempre più. Ma non è il caso di approfondire più di tanto, dato che lui vede veramente il mondo ai suoi piedi.

Si guarda un po' attorno e si accorge che è legato saldamente a una comoda poltrona P, solidale, ovviamente, con l'astronave. No, via quei legami di tipo "terrestre", lui vuole sentirsi libero di muoversi all'interno dell'abitacolo. E via anche quella porta che lo separa dallo spazio, dato che può indossare una tuta che gli permetterà di avere ossigeno a sufficienza anche nello spazio attorno a lui per un tempo lungo come l'intero viaggio.

Detto fatto: prima o poi deciderà di uscire, ma per adesso rimane seduto sulla sua poltrona comodissima. L'ha proprio progettata lui e l'ha voluta di un materiale che non causasse attriti fastidiosi, perfettamente liscio come la sua tuta. Il viaggio continua senza problemi e il magnate si sente sempre più a suo agio, ormai quasi convinto che lui sia veramente fermo e che sia lo spazio che si muova. Ovviamente, la sua velocità è esattamente quella dell'astronave e niente all'interno di essa gli appare muoversi, lui per primo: il sistema di riferimento non può che apparire fermo.

E' ora di rompere un po' la tranquillità di un viaggio che sta diventando monotono e comanda all'IA di fare qualcosa per ravvivare la situazione. Passano pochi istanti, ma che succede? Quella stupida macchina non ha eseguito assolutamente nessuna manovra. Tutto è sempre uguale a prima, lui continua a sentirsi fermo come tutti gli strumenti dell'astronave.

No, no, un momento ... qualcosa sta succedendo, non tutto è fermo! Chi si muove è proprio lui e sta dirigendosi senza alcuna esitazione verso il portello di uscita che aveva lasciato aperto. Accidenti! qualcosa lo spinge senza pietà, quasi volesse scacciarlo dall'astronave. Ma lui non è ancora pronto e non si è legato nessun modo all'astronave. Cerca di aggrapparsi a qualcosa ma la spinta è troppo violenta. In breve il nostro magnate si trova nello spazio e si allontana sempre di più dall'astronave. Come è stato possibile che solo lui si sia mosso? Ormai poco importa cercare di usare la ragione, dato che l'ossigeno non durerà per molto. E sono anche inutili i suoi improperi contro l'IA che lo ha cacciato dall'astronave. Accidenti non si era mai fidato degli uomini, ma non pensava di non doversi fidare nemmeno di una stupida macchina.

Bene, queste sono le condizioni in cui fanno la loro comparsa l'accelerazione centrifuga e quella centripeta, dato he l'astronave ha iniziato a muoversi di moto circolare uniforme. La sua velocità è rimasta invariata come modulo, ma non come direzione! Tuttavia, l'astronave e tutto ciò che è solidale con essa continuano ad apparire fermi nel sistema di riferimento dell'astronave. Se il magnate fosse legato alla poltrona si sentirebbe fermo, ma non lo è più! Il magnate, non può seguire l'astronave, ma è costretto a continuare nel suo moto rettilineo uniforme. Niente, infatti, lo ha disturbato, dato che niente lo lega all'astronave. Siamo di fronte a due moti: quello circolare dell'astronave e quello rettilineo uniforme del magnate. I due moti sono entrambi effettuati a velocità costante, ma hanno direzioni diverse.

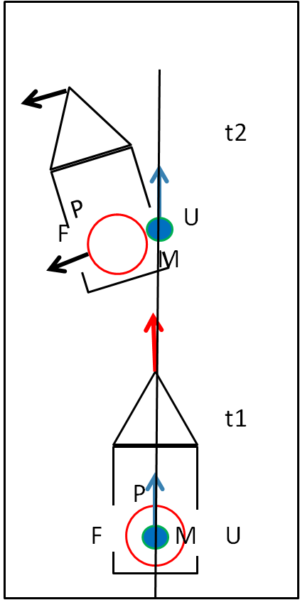
Vediamo in Fig. 1 quello che sta succedendo...

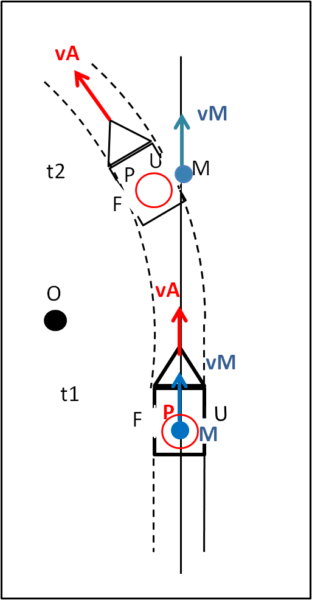
Al tempo t1, l'astronave e il magnate, slegato, mantengono il moto rettilineo uniforme e il magnate non si accorge di essere indipendente dall'astronave. La velocità dell'astronave e la sua sono esattamente le stesse come modulo e direzione. Tutto appare fermo al magnate. Al tempo t2, però, l'astronave subisce un "disturbo", ossia il suo motore le impone  una variazione della direzione, verso sinistra. La sua velocità compie, perciò, un angolo rispetto a quella precedente. Insieme all'astronave si muovono tutte le apparecchiature che sono vincolate ad essa. Tutto il sistema di riferimento astronave ha cambiato direzione, ma al magnate tutto ciò continua ad apparire perfettamente fermo. Il magnate, invece, non è vincolato all'astronave e quindi prosegue nella direzione della freccia azzurra. Non può che concludere che qualcosa lo sta spingendo verso l'esterno.

La Fig. 2 mostra cosa percepisce realmente il magnate.

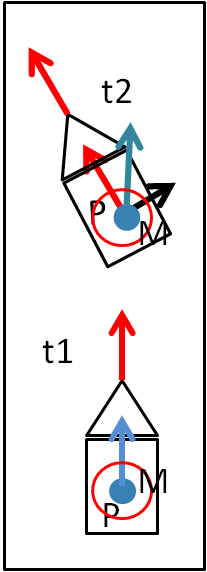
Il vettore rosso relativo al moto dell'astronave (e della poltrona P) fa un angolo rispetto a quello azzurro del magnate e possiamo facilmente separare il vettore  azzurro del magnate in due componenti: una che va nel verso dell'astronave e una che è perpendicolare alla direzione dell'astronave. La prima componente segue perfettamente il moto dell'astronave e quindi non causa nessuna variazione nel sistema di riferimento. L'altra componente, invece, è quella che sembra portare fuori il magnate dall'astronave, dirigendolo in direzione del portello e quindi del vuoto.

Il magnate si sente disturbato nel suo moto ed è costretto ad ammettere che rispetto a quello "fisso" dell'astronave, lui subisce una variazione di velocità che lo porta verso l'uscita, ossia sente un'accelerazione che va in direzione perpendicolare al moto dell'astronave, l'accelerazione centrifuga appunto.

La Fig. 3 ci mostra il tutto considerando immobile il sistema astronave.

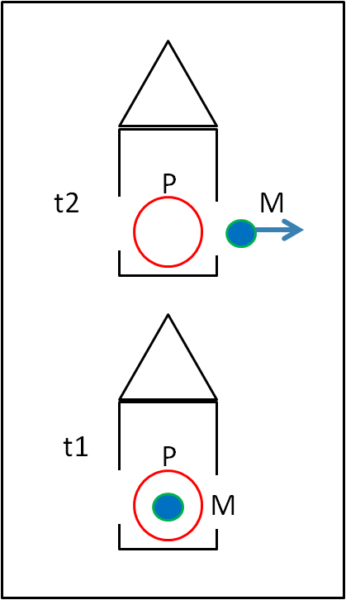
Le due astronavi, ai tempo t1 e t2, dovrebbero coincidere perché l'astronave viene considerata un sistema fisso, che non si muove. L'unico moto  apparente è quello verso destra del magnate. La parola "apparente" non è, però,  del tutto corretta ... Il magnate sente realmente la spinta che lo caccia verso il vuoto dello spazio ed ha pienamente ragione in quanto si sta spostando rispetto al sistema dell'astronave che assume fisso.

A questo punto non ci rimane che guardare tutto il viaggio dall'esterno, ossia attraverso un osservatore O che appartiene al  sistema di riferimento immobile dello spazio. Lui vede la Fig. 4, dove un'astronave viaggia di moto rettilineo uniforme con il magnate al suo interno.

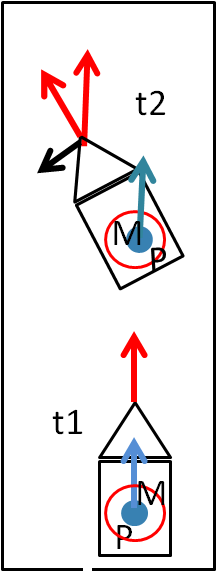
All'istante t2, però, vede che l'astronave piega verso sinistra iniziando un moto circolare uniforme. In altre parole, conclude che il moto dell'astronave è separabile in due componenti, una che continua come nell'istante precedente e una diretta verso sinistra, in modo perpendicolare alla traiettoria, che causa lo spostamento.  Il magnate, invece, non è vincolato all'astronave e perciò continua a muoversi soltanto di moto rettilineo uniforme.  In questo suo moto rettilineo incontra il portello che è aperto e quindi si trova nello spazio, mentre l'astronave continua a cambiare direzione. Il magnate non subisce alcun disturbo e prosegue a muoversi sempre nella stessa direzione. Lui non subisce alcuna accelerazione, ma è l'astronave che subisce una variazione di velocità, ossia un'accelerazione centripeta, diretta perpendicolarmente al moto dell'astronave, verso sinistra, come mostra la Fig. 5, dove le due astronavi sono viste dall'osservatore O veramente in posizioni diverse.

Le due accelerazioni sono una opposta all'altra, ma hanno lo stesso modulo. Qual è quella vera? Entrambe sono vere! Ciò che cambia non è l'accelerazione, ma solo il modo di descrivere il moto, ossia l'avventura, che rimane sempre la stessa.

Spero di avere accontentato Michele (e magari non solo lui...).