Questo articolo è inserito in Cinematica

 

Proseguiamo con i nostri esercizi di cinematica, passando ai casi bidimensionali. Chi la fa da padrone è il moto parabolico (o del proiettile), dove a un moto rettilineo uniforme si somma un moto uniformemente accelerato. Spesso e volentieri il secondo moto è quello relativo alla caduta di un corpo  a causa della gravità terrestre. Ne segue che l'accelerazione viene considerata costante e non è altri che la costante di gravitazione g = 9.8 m/s².

Facciamo un esempio che faccia uso di quasi tutte le le equazioni fondamentali.

(1) Siamo su un ponte che attraversa un fiume e lanciamo una pietra, con una velocità vo m/s, in modo tale da formare un angolo a con la linea orizzontale. Cronometriamo il tempo totale t_T in cui la pietra si  trova in aria, prima di cadere nell'acqua.

Vogliamo determinare

(I) La distanza s, rispetto al ponte, del punto di caduta nell'acqua.

(II) L'altezza h del ponte

(III) La massima altezza H raggiunta dalla pietra nel suo volo in aria? 

(IV) La velocità vf con cui la pietra cade in acqua?

Come al solito, sospendete la lettura se volete rispondere da soli...

 

Ricapitoliamo i dati in nostro possesso:

vo = velocità di lancio

a = angolo di lancio rispetto all'orizzontale

t_T = tempo totale passato in aria

Inseriamo la Fig. 1 che riassume sia i dati in nostro possesso sia quelli da calcolare (colorati in rosso).

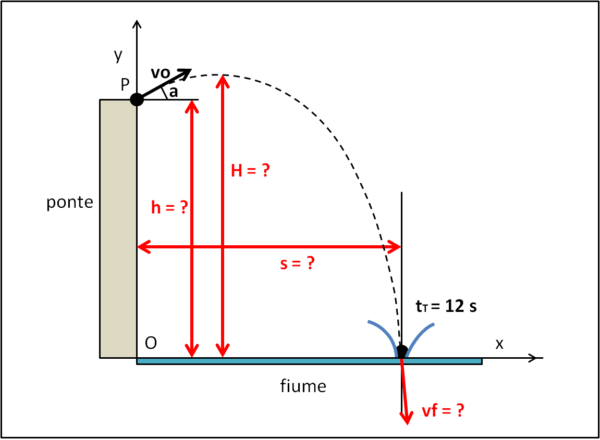
Prendiamo come origine O degli assi cartesiani  il punto posto sulla verticale del punto di lancio P e situato sul pelo dell'acqua.

Separiamo la velocità di lancio nelle sue due componenti lungo x e y:

vo_x = vo cos a

vo_y = vo sin a

Lavoriamo, per adesso, soltanto sulla componente verticale. Il moto della pietra è un moto uniformemente accelerato, dove al moto dovuto alla componente y della velocità iniziale si deve sommare il moto dovuto alla gravitazione.

Scriviamo la legge oraria della pietra per effetto di questo moto:

y = yo + vo_y t - 1/2g t²

Ciò che non conosciamo è yo, ossia l'altezza del ponte (yo = h, punto di lancio). Tuttavia, se poniamo t = t_T sappiamo che la pietra deve toccare l'acqua, ossia y = 0. Per cui:

0 = h + vo_yt_T - 1/2 gt_T²

Il segno meno tiene conto che l'accelerazione di gravità va verso le y negative, da cui:

h = - vo_yt_T + 1/2 gt_T²

che risponde alla domanda (II).

Consideriamo adesso solo la componente orizzontale della velocità. La gravità non influisce assolutamente, per cui siamo di fronte a un moto rettilineo uniforme, la cui legge oraria può scriversi:

s = s₀ + vo_x t

Poniamo t = t_T, e s₀ = 0, ricavando s

s = vo_x t_T

che risponde alla (I).

Dedichiamoci alla massima altezza raggiunta. Possiamo scrivere nuovamente la legge oraria del moto verticale:

y = y0 + vo_yt - 1/2gt²                          .... (1)

Questa volta, però, siamo interessati al tempo t relativo al raggiungimento della massima altezza y, ossia H. Nessun problema, basta derivare la (1), uguagliarla a zero e ottenere il valore t_M di t che corrisponde alla massima y.

dy/dt = vo_y - gt_M = 0

t_M = vo_y/g

A questo punto basta sostituire t_M nella (1) e ottenere il valore per cui la y raggiunge il massimo valore H:

H = h + vo_yt_M - 1/2gt_M² 

e abbiamo risposto anche alla (III)

Una piccola nota da non dimenticare. Siamo di fronte a un moto parabolico  nelle due dimensioni x e y, in cui la x e la y sono spazi  percorsi dalla pietra, ma siamo di fronte anche a un moto parabolico della coordinata y rispetto al tempo (moto orario). Non confondiamoli!

Non ci rimane che rispondere alla (IV).

Continuiamo a tenere separati i due moti, in modo da ricavare la velocità finale vf. La componente vf_x deve essere uguale alla vo_x, dato che il moto rettilineo è uniforme. La componente  finale della y si ricava, invece, dall'equazione che lega velocità e accelerazione nel moto uniformemente accelerato:

vf_y= vo_y - gt_T

Trovate le due componenti non ci resta che sommarne i quadrati e farne la radice quadrata:

vf =  -√(vf_x² + vf_y²)

Abbiamo, ovviamente, considerato il valore negativo, dato che la velocità finale è rivolta verso il basso.

Il gioco è fatto!

 

(2) Aggiungiamo un esercizio che ripete praticamente quello precedente, cambiando i termini noti e quello incognito.

Questa volta l'incognita è l'angolo a formato dalla direzione della velocità iniziale vo e dalla linea orizzontale.  Conosciamo, invece, la massima altezza raggiunta H e la distanza d percorsa dalla pietra lungo la linea orizzontale  (Fig. 2).

Notiamo che l'altezza del punto di partenza è uguale a quella di arrivo ed entrambi valgono zero.

Consideriamo il moto lungo y e applichiamo l'equazione di Torricelli alla componente v_y.

v_y² = vo_y ²- 2g y

Nel nostro caso v_y² corrisponde al punto di massima altezza in cui la velocità si azzera e y risulta essere H

0 = vo_y² - 2g H

vo_y² = 2g H   

ossia: 

vo² = 2g H/sin²a               .... (1)

Calcoliamo il tempo t in cui si raggiunge la massima altezza H, ossia la v_y = 0.

0 = voy - gt

t = vo_y/g 

t =  v0 sin a/g               .... (2)

Dal moto lungo x, sappiamo, però che:

s = s0 + vo_xt

nel nostro caso s = d/2  (corrisponde al punto di massima altezza) , ossia

d/2 = vo cos a t

al posto di t inseriamo quanto trovato nella (2)

d/2 = v0² sin a cos a/g

vo² = g d/(2 sin a cos a)                  .... (3)

Uguagliando la (1) e la (3), otteniamo:

2g H/sin²a = g d/(2 cos a  sin a)

4 g H cos a sin a = g d sin²a

Semplificando e dividendo entrambi i membri per sin a, abbiamo:

4 H cos a = d sina

sin a/cos a = 4H/d

tan a = 4H/d