Questo articolo è inserito in Cinematica

 

Moto circolare uniforme

Finora ci siamo occupati di moti mono o bidirezionali in cui il corpo in oggetto subiva uno o più moti rettilinei uniformi e/o uniformemente accelerati. Passiamo ora a un moto più complesso, quello circolare uniforme e a quello armonico che deriva direttamente da lui.

Ricordiamo che il moto rettilineo uniforme manteneva una velocità costante sia come modulo (l'intensità)  sia come direzione e verso. Il tutto era racchiuso nel suo nome: uniforme (a modulo costante) e rettilineo (direzione e verso  costanti).

Ora, invece, imponiamo che il corpo in movimento segua una traiettoria circolare attorno a un certo punto, pur mantenendo il modulo della velocità invariato. Nuovamente, essendo in cinematica, non ci interessa sapere come e perché il moto sia di questo tipo. Interessa solo saper descrivere le sue caratteristiche fondamentali.

Iniziamo a definire la sua velocità che, come modulo, assume la stessa formula del moto rettilineo uniforme:

v = s/t

Questa scrittura conferma che a parità di tempo trascorso lo spazio percorso rimane sempre lo stesso, ossia la classica definizione di velocità costante.

Sappiamo, però, che dopo un certo intervallo di tempo P, il corpo si ritrova esattamente nello stesso punto della sua traiettoria circolare. Quanto è lunga la  traiettoria percorsa in questo intervallo di tempo che abbiamo chiamato periodo P? Facilissimo da calcolare: essa è pari a 2πR, dove R è il raggio, ossia la distanza sempre uguale tra corpo che si muove e punto fisso O attorno a cui ruota. Possiamo, allora, permetterci di scrivere una banale proporzione:

Se il corpo, in un intervallo di tempo P, compie un tragitto pari a 2πR, in un intervallo di tempo t descrive uno spazio s che si ricava dalla relazione:

2πR/P = s/t

Ma s/t è proprio il modulo della velocità, che, quindi, può essere definita come:

v = 2πR/P                     .... (1)

Essa prende il nome di velocità tangenziale e vedremo tra poco perché. Resta indubbio il fatto che essa cambi direzione istante dopo istante dato che il percorso è circolare.

Potremmo, però, cercare di introdurre un nuovo tipo di velocità che non abbia problemi di direzione: la velocità angolare.

Definiamola come la variazione dell'angolo θ rispetto al tempo. Se il moto è circolare e uniforme questo valore rimane sempre costante. Sappiamo infatti che il percorso s effettuato in tempi uguali deve rimanere lo stesso. Ma esiste una ben nota relazione tra angolo e spazio percorso (che altri non è che l'arco di circonferenza corrispondente a θ):

s = R θ                 .... (2)

La (1) diventa:

v = s/t = Rθ/t = R (θ/t)

Chiamiamo, come abbiamo appena detto, θ/t = ω = velocità angolare. Ne segue che tra la velocità tangenziale e quella angolare esiste la relazione:

v = Rω                        .... (3)

Questa velocità ω ha dei grandi vantaggi rispetto a v. Essa è non solo costante per un certo percorso circolare, ma per tutti i percorsi circolari uniformi di centro O (Fig. 1).

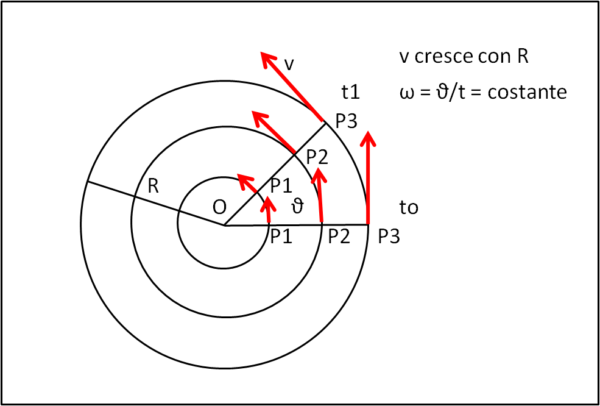
Qualsiasi sia R, la variazione di θ rispetto al tempo non cambia. In altre parole, tutti i corpi con la stessa velocità angolare si muovono in modo solidale tra loro, ossia stanno tutti sulla congiungente il centro con i punti P. Quella che cambia è solo la velocità tangenziale che è costretta ad aumentare al crescere di R (come ci dice la (3)) affinché il punto P riesca a rimanere sempre allineato con i punti delle altre circonferenze. Cambia lo spazio percorso nell'unità di tempo, ma non l'angolo.

Torniamo alla (1) e proseguiamo nell'analisi del nostro moto

Il modulo è costante come volevamo, ma cosa dire della direzione? Beh... questa cambia istante per istante, ma deve mantenere il corpo sulla circonferenza. In altre parole, la velocità deve avere una direzione che sia sempre tangente alla circonferenza, punto dopo punto. Il che vuole anche dire che la direzione della velocità è sempre ortogonale al raggio R che unisce il centro O con la posizione variabile di P.

Ma, allora, cos'è che vieta al punto di descrivere una traiettoria rettilinea? Un "qualcosa" che obbliga la velocità costante in modulo a variare costantemente la direzione. Questo "qualcosa" deve quindi essere un'accelerazione, dato che essa è proprio uguale alla variazione della velocità rispetto al tempo. Un'accelerazione che non cambi l'intensità della velocità (il modulo), ma che sia capace di cambiargli costantemente la direzione in modo che il corpo rimanga sempre alla stessa distanza dal centro O della traiettoria. Questo tipo di accelerazione viene chiamata accelerazione centripeta, ossia un'accelerazione che è diretta verso il centro (torneremo tra poco sul nome).

Attenzione: per adesso abbiamo solo visto che la velocità è sempre tangente alla traiettoria, ma non abbiamo ancora dimostrato che l'accelerazione che permette tutto ciò è diretta verso il centro.

In realtà, la risposta sarebbe immediata ricordando che la derivata di un vettore a modulo costante è un vettore perpendicolare ad esso. L'accelerazione è la derivata della velocità e quindi deve essere perpendicolare ad essa e, perciò, diretta verso il centro. Tuttavia, non abbiamo bisogno di introdurre le derivate, ma basta un po' di sana geometria elementare.

Consideriamo due punti della traiettoria P1 e P2 abbastanza vicini tra loro, che rappresentano due posizioni successive del corpo ruotante P, ai tempi t1 e t2.  Spostiamo P2 con la sua velocità v2 e portiamolo a coincidere con P1 che ha velocità v1 (Fig. 2).

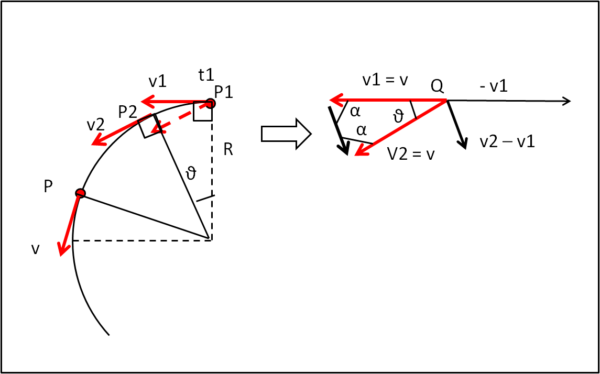
Otteniamo un triangolo sicuramente isoscele, dato che i lati v1 e v2 devono avere la stessa lunghezza. La variazione di velocità è data dalla differenza tra i vettori v2 e v1, ossia v2 - v1. I due angoli (uguali) sono anche uguali all'angolo formato da P1O e P2O, dato che è racchiuso tra rette perpendicolari ad essi (v2 e v1). A noi interessa sapere dove è diretta e quanto vale v2 - v1.

Ricordiamo che la variazione di velocità deve essere istantanea ossia dobbiamo far tendere l'angolo θ a zero, il che implica che la differenza t2 - t1 tenda anch'essa a zero. Ma cosa succede agli angoli α uguali tra loro? Sappiamo che la somma degli angoli di un triangolo vale 180°, ossia 2α + θ = 180°. Ma θ tende a zero, per cui 2α tende a 180 °, ossia  ogni angolo α tende a 90°. Ne segue che la differenza v2 - v1 tende ad essere perpendicolare rispetto alla velocità istantanea v. Ma la velocità v è sempre perpendicolare alla congiungente P con O e, quindi, la variazione v2 - v1 non può che essere diretta verso il centro. In poche parole, abbiamo dimostrato che la variazione di velocità rispetto al tempo (ossia l'accelerazione) è sempre perpendicolare al vettore velocità, istante per istante.

Un po' meno semplice è determinare il modulo di questa accelerazione, che, finalmente, abbiamo capito perché sia stata chiamata centripeta, ossia "verso il centro". Per superare questo piccolo ostacolo dobbiamo fare uso del concetto di limite che fino ad ora abbiamo solo sfiorato.

Scriviamo nuovamente ciò che abbiamo trovato in modo più matematico, dicendo che l'accelerazione non è altro che il limite, per t2 - t1 = Δt che tende a zero, della differenza di velocità Δv = v2 - v1 divisa per l'intervallo di tempo Δt. Questa scrittura è esattamente ciò che abbiamo dedotto poco fa:

a = lim _Δt→0 Δv/Δt

Moltiplichiamo e dividiamo il numeratore per 2.

lim _Δt→0 2(Δv/2)/Δt

Dal triangolo isoscele possiamo ricavare che:

Δv/2 = v sin (Δθ/2)

lim _Δt→0 Δv/Δt  = lim _Δt→0 2(v sin (Δθ/2)/Δt = 2v lim _Δt→0 sin (Δθ/2)/Δt                  (2v è una costante)

Moltiplichiamo e dividiamo l'argomento del limite per Δθ

lim _Δt→0 Δv/Δt = 2v lim _Δt→0 (sin (Δθ/2)/Δθ)/(Δt/Δθ) = 2v lim _Δt→0(sin (Δθ/2)/Δθ)(Δθ/Δt)

Riportiamo dentro al limite il 2

lim _Δt→0 Δv/Δt = v lim _Δt→0(sin (Δθ/2)/(Δθ/2))(Δθ/Δt)

Il limite del prodotto è uguale al prodotto dei limiti

lim _Δt→0 Δv/Δt = v lim _Δt→0(sin (Δθ/2)/(Δθ/2)) lim_Δt→0 Δθ/Δt

A questo punto dobbiamo ricordare un limite importantissimo, ossia il limite del rapporto tra il seno di un angolo e lo stesso angolo. Esso vale 1.

lim _x→0sin(x)/x = 1

Nel nostro caso quando Δt tende a zero, lo fa anche Δt, per cui

lim _Δt→0(sin (Δθ/2)/(Δθ/2)) = 1

Conosciamo già bene cosa rappresenta lim_Δt→0Δθ/Δt. Esso non è altro che la velocità angolare ω. Ne segue:

a = lim _Δt→0 Δv/Δt = v 1 ω

a = v ω 

oppure, ricordando la (3)

a = v²/R

oppure, ancora:

a = ω²R

Il procedimento che abbiamo adottato può risultare un po' complicato per qualcuno, per cui di seguito ne adottiamo un altro probabilmente più semplice, anche se fa sempre uso della trigonometria.

Torniamo al nostro triangolo isoscele che ha due lati uguali (v1 = v2 = v), che formano un angolo Δθ tra di loro. Il terzo lato è, ovviamente, Δv

Possiamo applicare al triangolo il teorema di Carnot:

Δv² = v² + v² - 2v² cosΔθ = 2v2 - 2v cosΔθ = v²(2 - 2 cosΔθ)

dividiamo ambo i membri per v²

Δv²/v² = 2(1 - cosΔθ)

Moltiplichiamo e dividiamo il secondo membro per  (1 + cos Δθ)

Δv²/v² = 2(1 - cosΔθ)(1 + cos Δθ)/(1 + cos Δθ) = 2 (1 - cos²Δθ)/(1 + cos Δθ) = 2 sin²Δθ/(1 + cos Δθ)

Per Δθ che tende a diventare piccolissimo, possiamo scrivere l'angolo al posto del seno, mentre il coseno tende al valore 1. Il secondo membro diventa:

2 Δθ²/(1 + 1) = Δθ²

Ossia:

Δv²/v² = Δθ²

Estraendo la radice quadrata da ambo i membri, otteniamo:

Δv/v = Δθ

Ricordando la (2), possiamo scrivere:

Δv/v = Δs/ R

Δv = Δs v /R

L'accelerazione è definita come rapporto tra variazione di velocità divisa per la variazione del tempo, ossia:

a = Δv/Δt =  (Δs/Δt )v/R

ma Δs/Δt non è altri che la velocità v, per cui:

a = v²/R

oppure, ricordando la (3)

a = v v/R = v ω = ω²R

 

Non ci rimane adesso che determinare la legge oraria del moto circolare uniforme. Per comodità useremo l'angolo θ per determinare la posizione del punto P lungo la sua traiettoria. E' poi immediato passare all'arco s, conoscendo il raggio R, ossia la relazione (2).

Per determinare questa legge è necessario introdurre il concetto di limite e derivata, anche se in modo estremamente banale.

La velocità angolare non è altro che la derivata dell'angolo rispetto al tempo:

ω = dθ/dt

ω dt = dθ

Questa, nel suo piccolo, è un'equazione differenziale a due variabili separabili, t e θ. Integriamola tra t = 0 e t  e tra θ = θ0 e θ per ricavare lo spazio percorso, che in questo caso è l'angolo corrispondente  all'intervallo di tempo trascorso.

∫₀^t ω dt = ∫_θ0^θ dθ

ω t = θ - θ0

θ= θ0 + ω t 

Essa è del tutto simile alla legge oraria del moto rettilineo uniforme, quando si consideri l'angolo percorso al posto dello spazio e la velocità angolare ω al posto della  v.

Non compare, ovviamente, l'accelerazione dato che essa è insita nel moto stesso.

 

Il moto circolare uniforme introduce subito un altro moto estremamente importante in fisica: il moto armonico semplice.

Consideriamo il punto P che ruota attorno all'origine O. Introduciamo le coordinate cartesiane x e y.

Il moto si ripete dopo il tempo necessario a far compiere 360° all'angolo θ, ossia dopo un periodo P. Possiamo perciò considerare il grafico solo in questo intervallo di tempo:

Al variare del tempo t varia l'angolo θ e l'ordinata del punto P non è altri che il raggio R moltiplicato per il seno di θ, mentre l'ascissa è il coseno moltiplicato per R (Fig. 3)

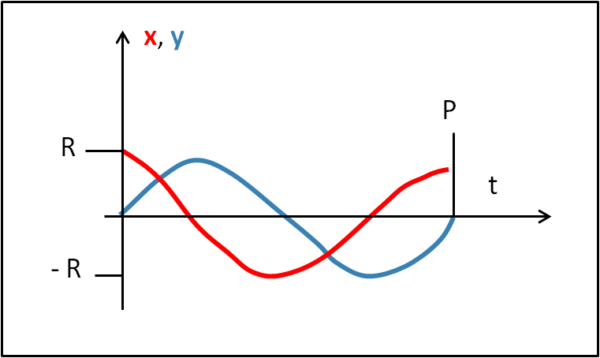
E' immediato tracciare la variazione di y e x rispetto al tempo. Esse descrivono delle sinusoidi spostate di 90° l'una rispetto all'altra. Possiamo perciò concludere che il moto armonico è la proiezione sul diametro di un moto circolare uniforme.

Nota 1:  Nel moto circolare uniforme nasce spontaneamente un'accelerazione. Non confondiamo, però, questa accelerazione con quella che deriva da un moto circolare uniformemente accelerato, equivalente al moto rettilineo uniformemente accelerato. In questo caso si introduce un 'accelerazione che va nella stessa direzione e verso della velocità tangenziale, ossia fa variare il modulo della velocità. Lo tratteremo la prossima volta.

Nota 2: A questo punto possiamo ribadire la differenza tra accelerazione centripeta e centrifuga. La prima è quella che nasce spontaneamente dal moto circolare e che viene osservata da un osservatore esterno. Lui vede il punto P con una certa velocità tangenziale di modulo costante che viene continuamente deviata nella sua direzione da un'accelerazione diretta verso il centro di rotazione. Il punto P, invece, si considera fermo (la sua velocità è costante in modulo) e quindi sente come disturbo tutto ciò che lo sposta rispetto a questa situazione. Lui è vincolato al centro della traiettoria circolare, ma non lo sa, e, quindi, la sua tendenza ad andare di moto rettilineo lo porta a essere spinto verso l'esterno rispetto al moto circolare. L'accelerazione centrifuga, perciò, può anche essere considerata "apparente" per chi vede il tutto da fuori, ma non lo è affatto per chi si sta muovendo di moto circolare uniforme: lui la sente e come!