Questo articolo è inserito in Cinematica

 

Non pensavo che questo problemino di cinematica risultasse così ostico. E pensare che bastava ricordarsi di Galileo e del suo piano inclinato per avere una risposta assolutamente quantitativa, dato che qualsiasi sia il percorso del boscaiolo, vincolato alle condizioni del problema, il risultato non cambia.

Ne segue che questa soluzione è altamente didattica perché mette in luce una caratteristica del moto sul piano inclinato che, probabilmente, non è conosciuta dai più...

Iniziamo con questa caratteristica che ci permetterà di concludere rapidamente il problema, aggiungendo un tocco di dinamica elementare. Inseriamo la Fig. 1.

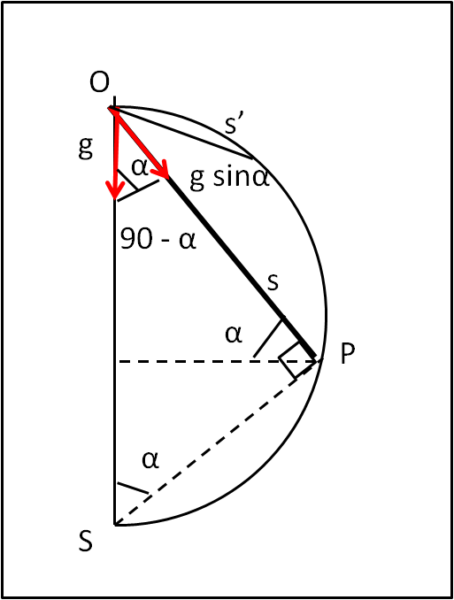
Disegniamo una semicirconferenza OPS. Tracciamo da O una corda qualsiasi OP di lunghezza s. Poniamo in O un corpo P che sia libero di strisciare lungo il piano inclinato OP, soggetto all'accelerazione g. Sul moto di P influisce solo la componente g sin α.

Scriviamo la legge oraria di P soggetto a un moto uniformemente accelerato, che parte da so = 0 con velocità vo = 0:

s = 1/2 g sin α t²

Ricaviamo il tempo necessario a P per raggiungere la circonferenza:

t = √(2s/g sin α)               .... (1)

Completiamo il triangolo rettangolo OPS tracciando il segmento PS.

Possiamo scrivere:

s = 2R sin α

Sostituiamo s nella (1) e otteniamo;

t = √(4 r sin α/(g sin α))

t = 2√(r/g)                        .... (2)

Ne segue che il tempo per partire da O e raggiungere la semicirconferenza è indipendente dalla lunghezza del tragitto s. Ad esempio, il tempo per percorrere s' è identico a quello necessario a percorrere s e, al limite, per cadere da O fino a S.

La relazione (2) risolve quasi immediatamente il nostro problema, Usiamo la Fig. 2 che schematizza la configurazione della gara.

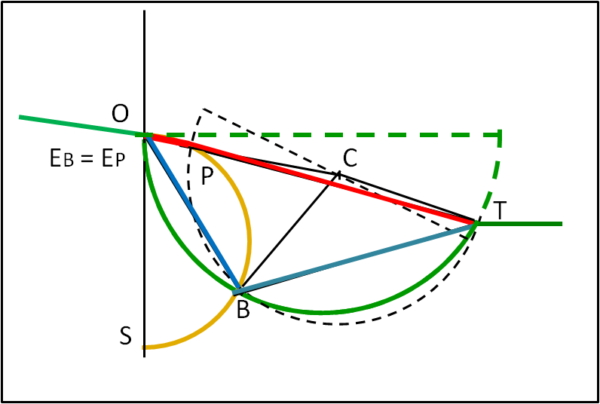
Il tragitto rosso è quello del principe, mentre quello azzurro è quello del boscaiolo. Essi arrivano nel punto O = EB = EP nello stesso istante e con la stessa velocità. Notiamo bene che il percorso "spezzato" azzurro tocca in un punto qualsiasi B la circonferenza verde che delimita proprio i punti in cui il boscaiolo può scendere.  La posizione di B può essere qualsiasi lungo questa semicirconferenza a patto che stia sempre più in  basso del traguardo T (il boscaiolo deve risalire).

Tracciamo da O il diametro verticale della circonferenza arancione che passi per B. Esiste una e una sola circonferenza con queste caratteristiche. Bene, a questo punto  confrontiamo la semicirconferenza di Fig. 1 con quella arancione di Fig. 2. Siamo nelle stesse identiche condizioni e possiamo concludere che qualsiasi sia la corda tracciata da O il tempo impiegato a percorrerla è una costante. Il che vuol dire che il tempo che il principe impiega per raggiungere P è identico a quello che il boscaiolo impiega ad arrivare in B.

Da questo momento in poi, il principe deve ancora percorrere il tragitto PT, mente il boscaiolo quello BT. Possiamo dimostrare in modo formale che il primo tragitto è sempre PIU' LUNGO del secondo, anche se visivamente il risultato è chiaro.

Tracciamo la circonferenza tratteggiata che passi per P, B e T.  C sia il suo centro. La corda PT sottende un angolo al centro PCT che è decisamente maggiore dell'angolo BCT sotteso dalla corda BT. Il che dimostra che BT è sempre più corto di PT.

Nella posizione relativa C e B dei due contendenti, B ha, quindi, davanti a sé un percorso nettamente più corto.

Ed ecco la ciliegina finale di dinamica...

Quando P e B giungono in O (posizioni EP ed EB) la loro energia meccanica è la stessa. Per la conservazione dell'energia essa deve rimanere costante. Il che significa che se il boscaiolo scende in B, più in basso di T, lungo il tragitto più corto BT, egli  possiede un'energia potenziale sicuramente più piccola di quella del principe. Ne segue che deve essere maggiore la sua energia cinetica, ossia la sua velocità.

Conclusione:

tragitto più corto e velocità maggiore: il boscaiolo vince sempre qualsiasi sia il punto B della semicirconferenza verde. che, ricordiamo, deve essere per ipotesi di partenza più basso di T.

Niente da fare... il piano inclinato è un pozzo senza fondo...