La corsa sugli slittini (soluzione analitica)

Il quiz sulla corsa con gli slittini  proposto recentemente da Vincenzo e  la relativa soluzione, squisitamente Galileiana,  costituiscono una esemplare pagina didattica sulla cinematica relativa al piano inclinato.

In questo breve articolo propongo  una soluzione analitica alternativa. Come sappiamo le soluzioni analitiche sono soluzioni formali, che non si accompagnano contestualmente al significato fisico, quindi Galileo  farà qualche bizza, tuttavia un valore aggiunto da questa soluzione è la possibilità di valutare la convenienza di ogni configurazione dello scenario di gara e  di individuare quella che sarebbe ottimale per il boscaiolo

Utilizzerò come riferimento il centro del cerchio come polo e l'angolo formato da un raggio rotante  a partire dal punto di inizio della discesa. La scelta di questo genere di  coordinate "polari", oltre a essere coerente con le gare sulla neve, è un modo semplice di schematizzare le relazioni tra le distanze percorse dai concorrenti .

Iniziamo il disegno fissando centro e raggio del cerchio che contiene i tre punti I (inizio) T(traguardo e P (punto di svolta). Il centro è C e il raggio è r.

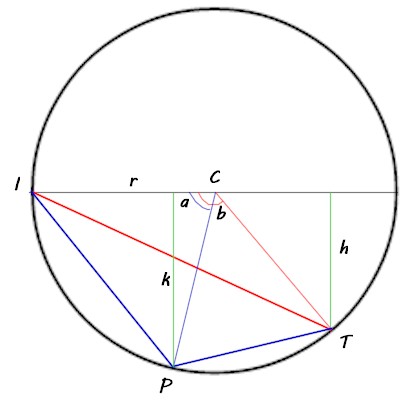
Fissiamo i tre punti avendo cura che P sia più in basso di T cosicché il boscaiolo veda che lo aspetta un tratto in salita per arrivare al traguardo.

Ora i punti lungo l'arco di cerchio in base all'angolo tra l'orizzontale e la retta che congiunge il centro C e il punto sulla circonferenza.

Indichiamo con la lettera “a” l'angolo che corrisponde al punto di svolta P e con la lettera “b” l'angolo che corrisponde al punto T.

Completiamo con le due quote “k” e “h” che rappresentano i dislivelli rispetto al punto di partenza I del Punto di svolta P e del punto del Traguardo T.

Le tre distanze IT (percorso diretto) , IP (tratto discesa) e PT (tratto salita) hanno le seguenti espressioni:

IT = 2r sen b/2 (IT è la base del triangolo isoscele ICT)

IP = 2r sen a/2 ( IP “ ICP)

PT= 2r sen (b/2 – a/2) ( PT “ PCT)

Le misure dei dislivelli sono le seguenti:

k = r sen a

h = r sen b

Esprimiamo ora le velocità iniziali e finali nei tratti IT IP e PT

tratto IT Vi= 0 Vf = radq(2gh)

IP = 0 = radq(2gk)

PT = radq(2gk) = radq(2gh) la stessa velocità finale del tratto IT

Possiamo quindi scrivere le velocità medie su tre tratti.

Velocità media su IT = ( 0 + radq(2gh) ) /2 = radq(2gh) / 2

Velocità media su IP = ( 0 + radq(2gk) ) /2 = radq(2gk) / 2

Velocità media su IT = (radq(2gk + radq(2gh) ) /2 = (radq(2gk) + radq(2gh)) / 2

Conosciamo le tre distanze e le velocità medie con cui sono percorse, quindi possiamo valutare i rispettivi tempi di percorrenza come rapporto tra spazio e velocità, esplicitando i valori di k e h.

Tempo IT = 2r sen (b/2) / radq (gr/2)* radq(sen b)

IP = 2r sen (a/2) / radq (gr/2) * radq(sen a)

PT = 2r sen( b/2 – a/2) / radq (gr/2) * radq(sen a) + radq( sen b)

Sottraiamo dal tempo IT la somma di IP e PT e troviamo il ritardo R del principe rispetto al boscaiolo. Se il risultato è positivo il boscaiolo è più veloce e vince.

Tempo IT – (tempo IP + tempo PT) = R < 0 vince il principe > 0 vince il boscaiolo

Se non ci interessa il valore dei minuti e secondi di distacco, ma vogliamo solo sapere chi vince, possiamo rimuovere tutti i coefficienti costanti comuni alle formule che si semplificano così:

R = sen b/2 / radq(sen b) - sen( a/2) / radq(sen a) - sen(b/2-a/2) / ( radq(sen a) + radq (sen b).

Il risultato è calcolabile per una data configurazione, ossia assegnati il punto del traguardo e il punto intermedio P possiamo sapere chi vince (e anche con quale distacco temporale), ma essendo indeterminata la configurazione (a parte il vincolo che P stia sotto T) occorre valutare tutte le posizioni possibili, quindi esaminare il grafico della funzione. Nel fare questo conviene fissare l'intervallo iniziando da Alfa = 0, ossia comprendendo l'intero arco e vedere l'andamento anche nel caso di punti P al di sopra di T. Sarà anche possibile trovare il massimo della funzione R , ossia la posizione di P in cui si realizza il distacco più consistente.

Nella figura seguente è rappresentato l'andamento di R nella ipotesi che  il traguardo T sia fissato in corrispondenza all'angolo b di 130°

Il valore di R è sempre positivo, quindi vince sempre il boscaiolo, qualsiasi sia il punto di svolta P.  Questa conclusione corrisponde a quanto emerge dalla soluzione cinematica.

La vittoria più schiacciante si realizza per P corrispondente all'angolo a=39,6°, come illustrato in questa figura:

Notiamo che in questa configurazione il punto P si trova al di sopra, di T, diversamente dalla ipotesi proposta nel quiz.

Cambiando la posizione del punto T ossia, fissando valori di b di volta in volta diversi, si ottengono grafici del tutto simili e si osserva che il punto di massimo si colloca generalmente scegliendo il punto P corrispondente un angolo “a” di circa un terzo dell'angolo “b”.

Naturalmente, per avere valori rigorosi, si potrebbe pensare derivare la funzione R, azzerare la derivata e trovare la coordinata che corrisponde al punto di massimo e poi anche il  conseguente valore del massimo, ma già dal grafico si può avere una idea abbastanza precisa.