Il quiz era piuttosto semplice e riguardava il confronto tra due moti circolari uniformi eseguiti con velocità angolare diversa.

Il primo moto è quello della lancetta piccola (delle ore). La sua legge oraria è:

θh = θoh + ωh t

dove ω è la velocità angolare pari alla variazione dell'angolo in funzione del tempo.

Vale la relazione:

ωh = 2π/P = 2π/12 = π/6

P è il periodo della lancetta delle ore ed è uguale a 12 ore.

Quindi, partendo dalle ore 0, abbiamo:

θh = 0 + π t/6 = π t/6

che vuole anche dire che in un'ora la lancetta percorre un angolo di π/6 = 30°

Per la legge oraria della lancetta dei minuti si ha:

θm = 0 + 2π t = 2π t

Infatti in un'ora viene percorso un angolo di 2π (ωm = 2π/1). Le due lancette partono assieme e noi siamo interessati alle configurazioni in cui:

θm - θh = π/2

Per cui:

2π t - π t/6 = π/2

da cui il tempo t della prima "quadratura" (la lancetta dei minuti va più veloce di quella delle ore):

t = (1/2)(6/11) = 0.2727 ore

Questo dato è sufficiente per svolgere l'intero esercizio, dalle ore 0 alle ore 12...

Infatti, la seconda "quadratura" si avrà quando l'angolo tra le due lancette è - 90° o, se preferite, quando è 270° = 3/2 π.

2π t - π t/6 = - π/2

t = - 0.27273 h

il che vuole anche dire che si avrà quando la lancetta dei minuti sta per raggiungere quella delle ore distanziata dello stesso intervallo temporale precedente.

E' più conveniente inserire 3/2 π (i tempi negativi sono un po' strani....) e, otteniamo, ovviamente:

2π t - π t/6 = 3π/2

t = 9/11 = 0.81818 h

Ma questo valore non è altri che tre volte 0.27273 h.

Una combinazione? Nemmeno per sogno! Ricordiamoci infatti che i due moti sono uniformi e quindi le differenze temporali variano linearmente. Indicando con Δt il valore costante 0.27273 h, la Fig. 1 illustra molto bene ciò che capita.

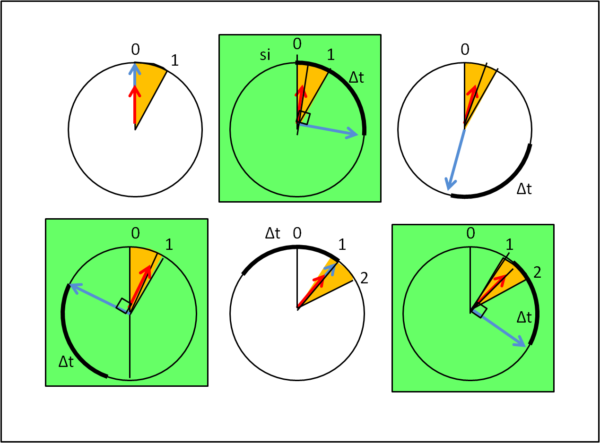
Vediamo chiaramente che per ogni aggiunta di Δt, la configurazione passa dalla quadratura all'allineamento delle lancette (in verso opposto e uguale).

Quanto sintetizzato nella figura è esattamente quanto detto con una semplice formula ricorrente nel commento di Andy del 6/11 alle 0:19, che ripropongo di seguito.  Prendendo i valori dispari dell'indice k siamo proprio nelle configurazioni di quadratura (colorate in verde). Ovviamente, 3/11 è proprio la nostra frazione di ora Δt.

k = 1    Ora = 00 + 1 × 3/11 = 00:16:21,82

k = 3    Ora = 00 + 3 × 3/11 = 00:49:05,45

k = 5    Ora = 00 + 5 × 3/11 = 01:21:49,09

k = 7    Ora = 00 + 7 × 3/11 = 01:54:32,73

k = 9    Ora = 00 + 9 × 3/11 = 02:27:16,36

k =11   Ora = 00 + 11 × 3/11 = 03:00:00

k =13   Ora = 00 + 13 × 3/11 = 03:32:43,64

k =15  Ora = 00 + 15 × 3/11 = 04:05:27,27

.......