Continuiamo nella nostra carrellata dei momenti angolari di solidi regolari. Passiamo  a quello di un cono pieno che ha per raggio di base R e per altezza h.

Poniamo in Fig. 1 il nostro cono con il vertice in basso e poniamo l'origine in questo punto con l'asse del cono come asse z.

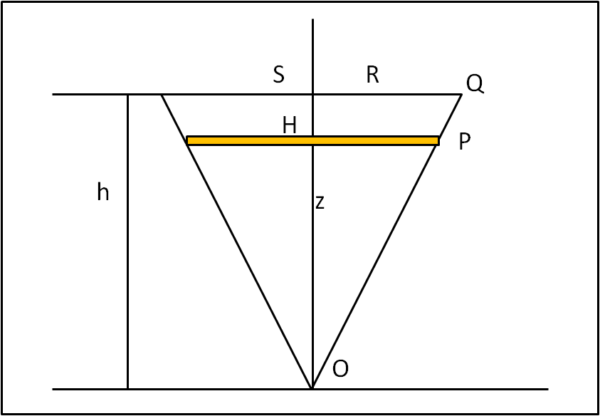
Prendiamo una fetta sottile del cono di altezza dz che si trovi a una distanza OH = z dal vertice. Dalla similitudine dei triangoli SQO e HPO possiamo scrivere:

HP = (R/h)z

Il suo volume infinitesimo risulta essere :

dV = π HP² dz = π (R²/h²)z² dz

e la massa

dm = π ρ(R²/h²)z² dz

Conosciamo, ormai, molto bene il momento d'inerzia di un disco sottile, che vale:

I = 1/2 m r²

nel nostro caso, il disco sottile ha, perciò, un momento d'inerzia pari a:

dI = 1/2 m HP² = 1/2 π ρ(R²/h²)z² dz · (R/h)²z²

dI = 1/2 π ρ(R⁴/h⁴)z⁴ dz 

Non ci resta che integrare per z che varia tra o e h

I = 1/2 π ρ(R⁴/h⁴)∫_o^h z⁴ dz

I = 1/2 π ρ(R⁴/h⁴) [z⁵/5]_o^h = 1/2 π ρ(R⁴/h⁴) h⁵/5 = 1/10 π ρ R⁴ h               .... (1)

La densità ρ del cono può scriversi come rapporto tra massa M e volume V

ρ = M/(πR² h/3) =  3M/πR² h

Sostituendo nella (1) otteniamo:

I = 1/10 π R⁴ h 3M/πR² h

I = (3/10) M R²

Il risultato ottenuto ci dice che il momento d'inerzia di un cono NON dipende dalla sua altezza, ma solo dalla massa e dal raggio di base.