Categorie: Matematica
Tags: divisione numero passaggi quiz rettangolo
Scritto da: Vincenzo Zappalà
Commenti:26
(QI) Chi va piano va sano e va lontano? **
Un quiz veramente ridicolo, lo ammetto. Tuttavia, lo propongo lo stesso per vedere chi riesce a trovare la soluzione con il minor numero di passaggi.
Nella figura disegniamo un rettangolo di lati 15 e 6.
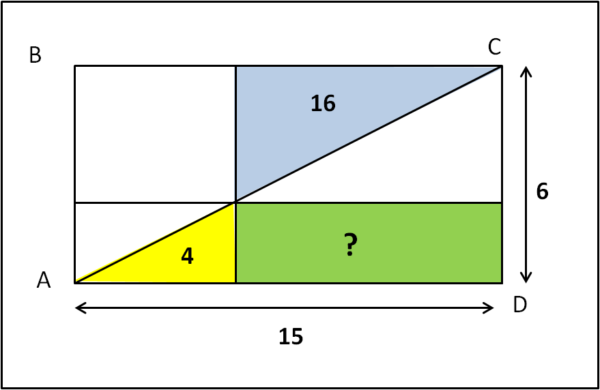
Lo dividiamo in 4 parti, tracciando la diagonale AC e due rette perpendicolari ai lati che identificano due triangoli rettangoli di area 16 e 4.
Determinare l'area del rettangolo verde.
Risparmiate passaggi, mi raccomando...






26 commenti
Caro Enzo, io farei così (lo metto in bianchetto per non mostrare il risultato e lasciare che altr@ possano rispondere senza venir influenzati dalla mia possibile soluzione).
Paolo
acci! sto diventando daltonico ?! Grazie Paolo...
C'è qualcosa che non quadra...
A prima vista, l'area del triangolo rettangolo bianco contrapposto a quello azzurro ha la stessa area 16,
per cui: Area verde = 15×6/2 - 16 - 4 = 25
Ma il triangolo giallo e quello azzurro sono simili (angoli opposti al vertice uguali) e le loro aree stanno nel rapporto di 4:1;
ciò significa che i lati del triangolo azzurro sono il doppio di quelli del triangolo giallo
ovvero GF = 2FE → 2FE + FE = 6 → FE = 2 ; GF = 4
allora AE = 2×(Area gialla)/2 = 4 → GC = 8 → AD = AE + GC = 4 + 8 = 12 anziché 15
e l'area verde sarebbe 8×2 = 16 anziché 25.
I dati forniti sembrano errati....
Area rettangolo = 90
area rettangolo verde = area quadrilatero bianco = (90-40)/2= 25
Lo dividiamo in 4 parti, tracciando la diagonale CD
Nel disegno sarebbe CA. Ma mi sembra di farti perdere solo tempo a correggere l'evidenza
Caro Professore, io dico che il primo passaggio è mettere a posto i dati del problema.
Area triangolo azzurro = 20 (invece di 16) area del giallo = 20/4 = 5 ( invece di 16/4 = 4)
Adesso si ragiona ...
la diagonale crea due triangoli uguali di area 90/2 = 45
a sinistra sopra il triangolo 5 ci sono 5 triangoli di area 5 ciascuno: totale 25
sommando il triangolo azzurro a questi 5 triangolini abbiamo 25 + 20 = 45 OK ! proprio metà giusta.
Tolgo da 90 ( 15*6) i 6 triangolini di sinistra da 5 ciascuno e resta 60 da dividere in tre rettangoli uguali di cui uno è il verde.
Morale, il triangolo verde ha area = 20
Ma non bastava dire subito che il lato di base del rettangolo è 2/3 di 15 e il lato altezza è 1/3 di 6 ?
così abbiamo subito area = 10 * 2 = 20
poi se i dati delle altre aree sono state scritte sbagliate... che importa?
Lei cosa ne pensa , Prof ?
Cerea !
Come mi aspettavo... ma, io ho chiesto "quanti passaggi per risolvere il problema". La soluzione potrebbe anche essere "problema impossibile" e io vorrei sapere che passaggi si devono fare per dimostrarlo . Però bisogna dimostrarlo...
Ad esempio, potrei dire "problema impossibile perché ci sono dei dati in più del necessario, discordanti tra loro"
ops... è partito il commento senza volerlo...
Andy ha dimostrato l'impossibilità del quiz applicando due metodi ed è una strada con un certo numero di passaggi.
Maurizio ha subito detto che i dati non sono giusti e poi ha modificato i valori... Ma dovrebbe dire che passaggi ha fatto per dire che i dati erano sbagliati...
Il quiz è un quiz dato alle olimpiadi e si basava proprio sulla capacità di dimostrare l'inconsistenza del problema.
La strategia che ho usato io è quella di prendere solo i dati necessari escludendone uno qualsiasi di quelli di troppo e verificare che quello escluso ha un valore errato.
Insomma, non fidarsi mai di un problema che dà troppi dati... in tal caso è meglio andare piano, ma lontano....
Spero di essere capito nelle mie intenzioni!
La richiesta del quiz era questa: Determinare l'area del rettangolo verde.
Sicuramente Oreste l'ha determinata e ha fatto un solo passaggio, ignorando i dati delle aree.
Dopo che me lo ha spiegato ( in privato, prima di pubblicare il suo commento) è stato facile ricalcolare le aree correggendo i valori sbagliati ( oltre che inutili).
triangolo azzurro base = 10 e altezza = 4 area = 20
triangolo giallo base = 5 e altezza = 2 area = 5
Facile no ?
Naturalmente ho pubblicato il mio commento prima di quello di Oreste.
In definitiva l'unico dato da considerare è che il rapporto tra le aree dei due triangoli, giallo e azzurro, è 1 a 4 , come ha messo bene in evidenza Andy, senza la necessità di conoscere i valori, giusti o sbagliati, delle due aree.
In maggior dettaglio:
area triangolo azzurro = 4 * area triangolo giallo
quindi i lati del triangolo azzurro valgono il doppio di quelli del triangolo giallo
15 corrisponde a base azzurro + base giallo = 3 basi giallo
6 corrisponde ad altezza azzurro + altezza giallo = 3 altezze giallo
base giallo = 15/3 = 5 e altezza giallo = 6/3 = 2 area giallo = 5*2/2 = 5
area azzurro = 4 volte 5 = 20
caro Mau,
tu dici:
Sicuramente Oreste l'ha determinata e ha fatto un solo passaggio, ignorando i dati delle aree.
Ciò vorrebbe dire che Oreste ha lavorato solo sui lati 6 e 15 per determinare l'area verde? Ma come ha fatto?
In realtà, Oreste ha anche scritto:
Ma non bastava dire subito che il lato di base del rettangolo è 2/3 di 15 e il lato altezza è 1/3 di 6 ?
Ma è un indovino o cosa?
Oreste indovino?
Area triangolo azzurro = 4 * area triangolo giallo
quindi i lati del triangolo azzurro valgono il doppio di quelli del triangolo giallo
15 corrisponde a 3 basi giallo
6 corrisponde a 3 altezze giallo
E pertanto..
base rettangolo = 2/3 di 15
altezza rettangolo 1/3 di 6
Conclusione Oreste non è un indovino, peccato!
Forse ho interpretato male il problema, ma mi sembra ci siano requisiti incompatibili tra loro.
La mia interpretazione è questa.
I triangoli colorati ed il triangolo ADC sono simili.
Chiamo h1 e b1 i cateti del triangolo giallo e e h2 e b2 i cateti di quello celeste.
h1/b1=CD/AD=2/5 e h1*b1=8 seguirebbe che h1=4/√(5) e b1=2√(5)
Poiché h2=6-h1 e b2=15-b1 è già determinato anche il valore di h2*b2 a circa 44,33... che invece per il requisito sull'area azzurra dovrebbe essere 32.
In pratica, fermo restando il rettangolo 15×6,
bisogna cambiare, alternativamente, i valori delle aree dei triangoli rettangoli giallo e azzurro;
(i triangoli rettangoli giallo, azzurro e ACD sono tutti simili tra loro).
Se tengo fisso il valore 16 dell'area del triangolo rettangolo azzurro, devo variare il valore dell'area del giallo:
Se tengo fisso il valore 4 dell'area del triangolo rettangolo giallo, devo variare il valore dell'area dell'azzurro:
Correzione: nella prima figura i rapporti sono tra ACD e FGC...
Sorry!....
Però, Andy, tenendo fisso un triangolo e cambiando l'altro si perde sempre il rapporto di 1 a 4 tra le loro aree.
Siamo tutti d'accordo, credo, che esiste una incongruenza tra i dati.
Se consideriamo validi i valori dei lati di tutta la figura, base 15 e altezza 6, allora i valori delle aree dei triangoli sono incompatibili.
I valori delle due aree non possono essere entrambi corretti.
Nella ipotesi di Andy uno dei due valori è corretto e l'altro sbagliato.
Nella ipotesi di Oreste il rapporto tra le aree è corretto ma ambedue i valori dichiarati sono sbagliati.
Non penso si possa dimostrare che una delle due ipotesi è più giustificata dell'altra.
C'è poi anche il caso che ambedue le aree siano diverse da quelle dichiarate e il loro rapporto non sia 1 a 4.
La determinazione dell'area del rettangolo dipende dalla ipotesi prescelta. (arbitrariamente)
Ma potrebbero anche essere giuste le aree dei due triangoli e sbagliate le misure dei lati del rettangolo complessivo.
Anche in questo caso proliferano le possibilità
potrei avere un triangolo azzurro di area 16 data da: base 8 e altezza 4 . Quindi un triangolo giallo di base 4 e altezza 2. In questo caso le misure globali sarebbero 12 x 6
oppure un triangolo azzurro di area 16 data da : base 16 e altezza 2. Quindi un triangolo giallo di base 8 e di altezza 1. In questo caso le misure globali sarebbero 24 x 3
O ancora infinite altre combinazioni.
La risposta al quiz è che non si può determinare nulla.
Andy ha capito cosa intendo dire...
Poco mi interessa quale sia il dato sbagliato, ma bisogna dimostrare che uno deve esserlo di certo.
Se non pensassi a questo potrei trovare il solito 25.
La mosca al naso deve saltare quando mi accorgo senza fare calcoli che i dati sono ESUBERANTI per risolvere il problema. Mi devo chiedere come mai? Considero allora quelli sufficienti, ad esempio, 15, 6 e 16 per l'area (basterebbero loro...) e risolvo il quiz, verificando, però, che il 4 sia un valore ammissibile. Se trovo un valore diverso poco m'importa di trovare un rettangolo diverso: il problema come è stato dato è IMPOSSIBILE, ossia non può essere reale!
Non ho chiesto, infatti, quali siano i valori corretti per avere una soluzione... ma la SOLUZIONE al quiz con i dati originari!
Beh.... certo che se usa il rapporto delle aree la cosa è diversa. Ma tu dici:" Sicuramente Oreste l'ha determinata e ha fatto un solo passaggio, ignorando i dati delle aree." Il che vuol dire che non ha tenuto conto dei valori delle aree e, quindi, nemmeno del loro rapport0. E invece, poi mi dici che ha usato il rapporto... Insomma, una cosa o l'altra. Oreste ha una doppia personalità?
Direi che il tutto è riassunto nella frase di Andy:
Se tengo fisso il valore 16 dell'area del triangolo rettangolo azzurro, devo variare il valore dell'area del giallo.
Il che vuol dire che il problema è impossibile, dato che fissa anche l'area gialla.
Bastava dire: problema impossibile perché almeno un dato è sbagliato. Non posso sapere quale sia e, quindi, non so cosa dovrei risolvere.
E questa è stata giudicata la risposta più logica.
Eppure alle 13.56 lo avevo spiegato in modo chiaro ....
Nella ipotesi di Oreste il rapporto tra le aree è corretto ma ambedue i valori dichiarati sono sbagliati.
Si vede che non lo hai visto.
Caro Mau,
Sicuramente l'intervento sia tuo che di Oreste ha creato confusione... Resta il fatto che lui ha detto di non curarsi delle aree, mentre invece ha giudicato corretto il loro rapporto. La cosa non mi quadra: se non considero le aree non devo nemmeno considerare il loro rapporto.
Questa frase è stata detta da Oreste (così, almeno, dici tu):
Sicuramente Oreste l'ha determinata e ha fatto un solo passaggio, ignorando i dati delle aree.
E, invece, lui dice direttamente:
Area triangolo azzurro = 4 * area triangolo giallo
Il che vuol dire che le ha considerate e come!
Comunque, alla fine ci siamo capiti, ma Oreste crea sempre dei problemi aggiuntivi...
Lo dici tu stesso...
Ma potrebbero anche essere giuste le aree dei due triangoli e sbagliate le misure dei lati del rettangolo complessivo.
E questo sarebbe stato un metodo corretto per dire che il problema era impossibile. Un'alternativa alla descrizione di Andy...