Questo articolo è inserito in Cinematica

 

Così come il moto rettilineo uniforme poteva subire un'accelerazione costante, così può succedere per il moto circolare uniforme. L'accelerazione che viene imposta ha la direzione della velocità tangenziale e, quindi, modifica il modulo di questa velocità che deve, comunque far restare il punto P sulla circonferenza. Ne seguono alcune caratteristiche generali.

la velocità tangenziale cambia sia il modulo che la direzione.

La velocità angolare cambia costantemente, dato che un aumento della velocità tangenziale implica di percorrere, a parità di tempo, un angolo maggiore.

L'accelerazione tangenziale è costante in modulo, ma varia costantemente in direzione dato che è sempre parallela alla velocità tangenziale

L'accelerazione centripeta (che niente ha a che fare con l'accelerazione impressa tangenzialmente) è costretta a variare da punto a punto, in quanto cambia il modulo della velocità tangenziale e di conseguenza l'accelerazione centripeta che valeva

ac = v²/R

oppure

ac = ω²R

dove abbiamo visto che la velocità angolare varia istante per istante.

L'unica grandezza che rimane costante nel tempo è l'accelerazione tangenziale a_T applicata al punto P. Essa, però, rimane costante in modulo ma non in direzione dato che è costretta a  seguire la stessa variazione direzionale della velocità tangenziale.

Possiamo, infine,  introdurre  un'accelerazione angolare α che rimane costante.

La Fig. 1 riassume queste grandezze.

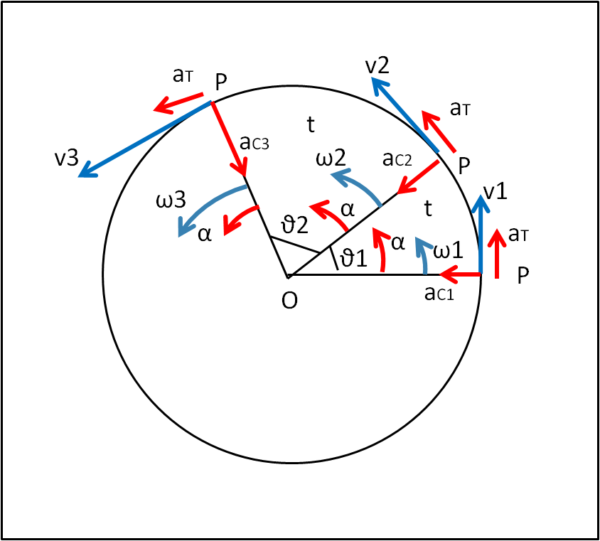
Come vediamo, esistono due vettori accelerazione perpendicolari tra loro, quello tangenziale a_T e quello  relativo alla accelerazione centripeta a_C. Possiamo sommare i due vettori e ricavare il modulo dell'accelerazione totale a_tot

at_ot = √(a_T² + a_C²)

l'accelerazione  angolare , costante, è uguale alla variazione della velocità angolare divisa per il tempo.

α = Δω/Δt

Ma  la velocità angolare  è data da:

ω = R v

per cui

α = R Δv/Δt

Ricordando che

a_T = Δv/Δt

otteniamo:

α = R a_T

che è un'importante relazione tra una grandezza vettoriale e una angolare. Essa conferma, ovviamente, che se è costante a_T deve esserlo anche α.

Ricaviamo ora, attraverso derivate e integrali veramente banali, la legge oraria del moto uniformemente accelerato.

Scriviamo l'accelerazione angolare in termini di variazione infinitesima di ω rispetto al tempo:

α = dω/dt

ossia

dω = α dt

Poniamo il tempo iniziale uguale a zero, a cui corrisponde una velocità angolare ω₀, e integriamo ambo i membri:

∫_ω0^ω dω = α∫₀^t dt

ω - ω₀ = αt

ω = ω₀ + αt

Questa è la relazione che esprime la velocità angolare in funzione del tempo.

Essa può anche essere scritta come:

dθ/dt = ω₀ + αt

Oppure

dθ = (ω₀ + αt) dt

Integriamo ambo i membri

∫_θ0^θ dθ = ∫₀^t (ω₀ + αt) dt

∫_θ0^θ dθ = ∫₀^t ω₀ dt + ∫₀^tαt dt

θ - θ₀ = ω₀ t + α t²/2

da cui la legge del moto

θ = θ₀ + ω₀ t + α t²/2

che del tutto simile alla legge oraria del moto rettilineo uniformemente accelerato

s = s₀ + v_o t + a t²/2

dove al posto dello spazio si consideri l'angolo θ e al posto della velocità e accelerazione lineare si considerino velocità e accelerazione angolare.

Leghiamo le due leggi trovate nel solito sistema:

ω = ω₀ + αt

θ = θ₀ + ω₀ t + α t²/2

Ricaviamo il tempo dalla prima e inseriamolo nella seconda (o viceversa), ottenendo:

ω² = ω₀² + 2 α(θ - θ₀)

che è la cosiddetta equazione senza tempo, del tutto simile, ovviamente, all'equazione di Torricelli:

v² =  v₀² + 2a(s - s₀)