Questo articolo è inserito in Cinematica

Ecco un simpatico problemino in cui facciamo un passo in avanti: non solo entra in gioco l'accelerazione, ma lo fa aumentando in modo uniforme, ossia siamo di fronte a ciò che si chiama strappo o, in inglese, jerk. Ne abbiamo già parlato QUI, ma adesso vedremo di affrontarlo senza complicarci troppo la vita. Ecco il problema:

L'accelerazione di un oggetto cresce in modo uniforme ed essa vale a₀ al tempo zero, mentre raggiunge il valore a₁, al tempo t₁. La velocità al tempo zero vale v_o.

Domanda 1:

Quanto vale la velocità v_t dell'oggetto al tempo generico t ?

L'accelerazione varia in modo uniforme e ci conviene inserire in un grafico (Fig. 1) le informazioni che abbiamo. Sull'asse delle ordinate poniamo l'accelerazione, mentre sull'asse delle ascisse inseriamo, come sempre, il tempo.

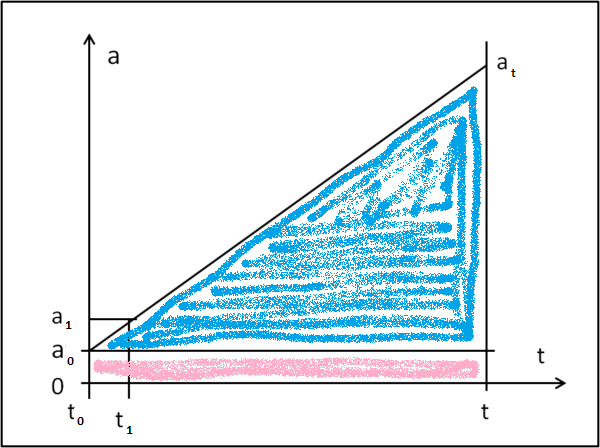
L'accelerazione, variando in modo uniforme, viene ovviamente descritta da una retta. Essa vale a₀ al tempo t = 0 e a₁ al tempo t = t₁.

E' immediato scrivere:

(a₁ - a₀)/(t₁ - 0) = (a_t - a₀)/(t - 0)

dove t è un tempo generico e a_t l'accelerazione corrispondente. Da questa semplice proporzione si deriva la variazione di accelerazione  a_t - a_o

(a_t - a₀) = (a₁ - a₀) t/t1             .... (1)

Sappiamo benissimo che l'accelerazione è la derivata della velocità. Ne segue che la velocità non è altro che l'integrale dell'accelerazione. Nel caso in esame non è necessario calcolare l'integrale, ma basta considerare come variazione di velocità l'area sotto la retta che rappresenta l'accelerazione, nell'intervallo t - 0. In poche parole, l'area del rettangolo rosa più l'area del triangolo azzurro:

v_t - v₀ = a₀t +1/2 (a_t - a₀) t

dalla (1)

v_t = v₀ + a₀t + 1/2(a₁ - a₀) t²/t₁ 

che è l'espressione richiesta.

 

Diamo ora qualche valore numerico:

a₀ = 2 m/s²

a₁ = 3 m/s²

t₁ = 1 s

t = t₂ = 10 s

v₀ = 1 m/s

Domanda 2

Determinare lo spazio percorso nel primo secondo e tra 9 e 10 secondi

Riprendiamo la relazione appena trovata che lega la velocità con il tempo:

v_t = v₀ + a₀t + 1/2(a₁ - a₀) t²/t₁ 

e sostituiamo i valori numerici

v_t = 1 +2t + 1/2 t²

Questa relazione ci dice che il grafico della velocità in funzione del tempo è una parabola, che possiamo facilmente disegnare. In Fig. 2 riportiamo una rappresentazione solo qualitativa, dato che con i valori in nostro possesso il grafico avrebbe problemi di inserimento.

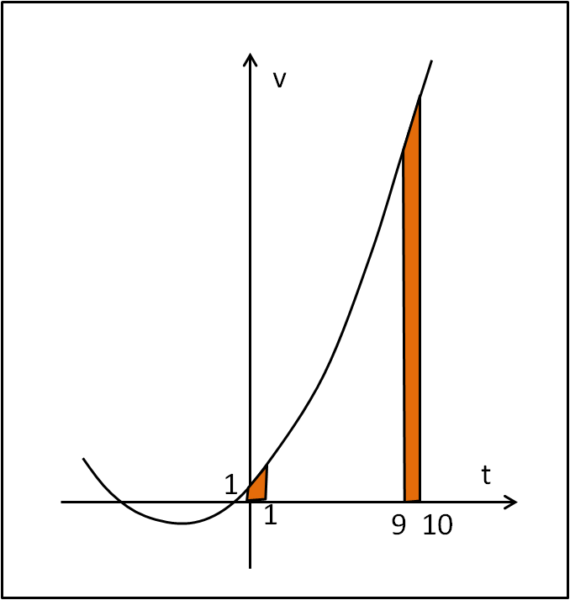
Ricordiamo che lo spazio percorso è l'integrale della velocità, per cui basterebbe calcolare gli integrali di questa relazione tra 0 e 1 secondi e tra 9 e 10 secondi, ossia le aree colorate in arancione.

La limitatezza degli intervalli di tempo richiesto e il tipo di curva, di ci permettono di risolvere il problema approssimando i tratti di parabola con tratti rettilinei. In altre parole, basta trovare l'area dei due trapezi di Fig. 2. Per far ciò, dobbiamo ancora trovare i valori della velocità nei vari estremi temporali:

v₀ = 1     m/s     (dato del problema)

v₁ = 1 + 2 + 0.5 = 3.5 m/s

v₉ = 1 + 18 + 81/2 = 59.5 m/s

v₁₀ = 1 + 20 + 100/2 = 71 m/s

Abbiamo tutti i dati per calcolare le aree riportate in Fig. 3,  dove abbiamo separato i due tratti di parabola per riportare le  misure corrette.

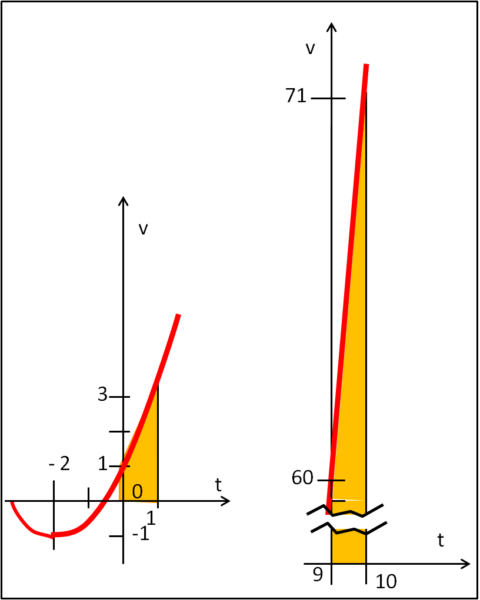
s₁ = (v₀ + v₁) (t₁ - t_o)/2 = 4.5/2 = 2.25 m

s₂ = (v₁₀ + v₉)(t₁₀ - t₉)/2 = 65.25 m

Il problema potrebbe finire qui, ma a noi non fanno certo paura gli integrali definiti, soprattutto se le funzioni sono composte da potenze della variabile x. Nel nostro caso la funzione è una funzione di secondo grado e, in particolare, una parabola.

Non ci resta allora che calcolare l'integrale della nostra parabola nell'intervallo temporale 0-1.

s₁ = ∫₀¹(1 + 2t + t²/2) dt = ∫₀¹ dt+ 2∫₀¹t dt+ 1/2∫₀¹ t² dt

s₁ = [t]₀¹ + 2[t²/2]₀¹ + 1/2[t³/3]₀¹ = 1 +1 + 1/6

s₁ = 2.167 m

s₂ = ∫₉¹⁰(1 + 2t + t²/2) dt = ∫₉¹⁰ dt+ 2∫₉¹⁰t dt+ 1/2∫₉¹⁰ t² dt

s₂ = [t]₉¹⁰ + 2[t²/2]₉¹⁰ + 1/2[t³/3]₉¹⁰ = 1 + 19 + 45.167

s₂ = 65.167 m

Ovviamente, l'errore ottenuto con l'approssimazione è minore per tempi più alti, quando la curva è praticamente assimilabile a una retta.

Beh... direi che era proprio facile e capisco perché i più esperti non siano intervenuti.  Mi stupisco, però, che nessuno abbia voluto provare: mancanza di tempo o paura di sbagliare? Il primo caso è più che accettabile, il secondo non molto. Ricordiamoci che è più facile imparare sbagliando che evitando i problemi.