(QI) Pochi dati, ma buoni! **

07/12/23

(QI) Pochi dati, ma buoni! **

Categorie: Matematica Tags: Scritto da: Vincenzo Zappalà Commenti:12

Dopo nuclei che si divertono a rompersi e a unirsi, treni che fischiamo, evoluzione cosmologica, torniamo alla cara geometria (Euclide si è un poco alterato della vostra poca passione a riguardo...).

Il problema da risolvere è piuttosto semplice, ma abbisogna di un minimo di fantasia, almeno, per come l'ho pensato io...

Consideriamo due assi cartesiani x e y, e disegniamo un triangolo isoscele QUALSIASI che abbia la base posta sull'asse delle x come mostra la figura che segue.

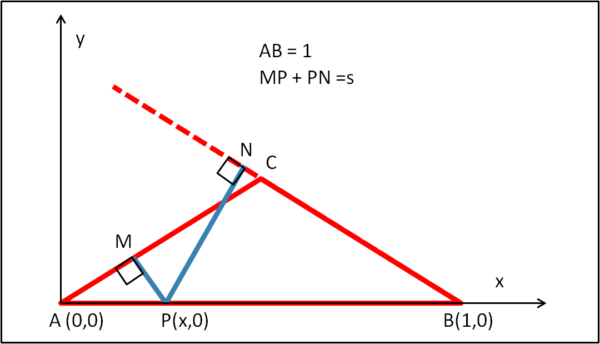
Prendiamo un punto P QUALSIASI sulla base del triangolo. Tracciamo da P le perpendicolari ai due lati uguali del triangolo isoscele o, se necessario, sul loro prolungamento e chiamiamo M e N i punti di intersezione.

Poniamo

AB = 1

PM + PN = s (noto).

Si chiede di calcolare l'area del triangolo, in funzione di x.

Un consiglio: provate a risolvere il problema con triangoli sia acutangoli che ottusangoli...

P.S.: Vediamo se qualcuno riesce a risolverlo in modo diverso (e migliore) dal mio.

QUI la soluzione

Articoli correlati

12 commenti

  1. leandro
    09/12/2023 at 13:05

    MAP è simile a NPB

    h2/h1 = (1-x) /x

    1/x = h2/h1 +1 = ( h2+h1 ) / h1

     

    h1 = s x

    ma MAP è simile a HCA

    h1 /l1 = h / (1/2)

    h = 1/2 h1/l1 = 1/2 s x /l1

    ma

    l1 = \sqrt{x^{2}-h_{1}^{2}}

    quindi

    h = \frac{1/2 s x }{\sqrt{x^{2}-h_{1}^{2}}}

    sostituendo l'espressione di h1

    h = \frac{1/2 s x }{\sqrt{x^{2}-(sx))^{2}}}

    h = \frac{1/2 s }{\sqrt{1-s)^{2}}}

    Area = 1/2 h = \frac{1/4 s }{\sqrt{1-s)^{2}}}

    ps: fatto senza AI.

     

     

     

     

     

  2. Vincenzo Zappalà
    09/12/2023 at 18:23

    caro Leandro, controlla bene la radice quadrata... mi dà l'idea che tu abbia scritto (1 - s)2 invece di (1 - s2).

    Se sei d'accordo ti invito a trovare una soluzione ancora più semplice, che fa tesoro di una "strana" e poco conosciuta proprietà del triangolo isoscele.

  3. leandro
    09/12/2023 at 22:47

    sì,    in effetti l'espressione corretta è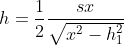 h = \frac{1}{2} \frac{s x}{\sqrt{x^{2}-h_{1}^{2}}}

    da cui

    Area = \frac{1}{2} h = \frac{1}{4} \frac{s}{\sqrt{(1- s)^{2}}}

    Per il triangolo sto pensando alle due altezze relative ai lati obliqui, vediamo un po'

     

  4. Vincenzo Zappalà
    10/12/2023 at 08:10

     

    Caro Leandro,

    Mi sa che continui a sbagliare...

    Se l'espressione corretta è

    h = 1/2 sx/V(x2 - h12)

    allora il risultato è diverso dal tuo...

    h = 1/2 sx/V(x2 - s2x2) = 1/2 sx/V(x2(1 - s2)) =1/2 sx/(xV(1 - s2)) = 1/2 s/V(1 - s2)

     

    In ogni modo, vi è un sistema ancora più semplice che non ha assolutamente  bisogno di spaccare s in h1 e h2

  5. leandro
    10/12/2023 at 10:44

    Mi ero dimenticato il giroscopio laser. In ogni triangolo isoscele la somma delle due altezze

    relative agli obliqui è costante (cioè s).

    Nel caso particolare in cui le altezze si trovino a metà della base (unitaria) , il triangolo si

    divide in due triangoli rettangoli uguali la cui altezza è s/2.

     

  6. Vincenzo Zappalà
    10/12/2023 at 11:14

    Caro Leandro...

    dai le risposte a pezzi e il risultato continua a non essere giusto.

    1. confermi che il tuo ultimo risultato è sbagliato ?
    2. dimostra che la somma delle altezze relative ai due lati uguali è sempre la stessa
    3. trova l'area, sfruttando quest'ultima relazione

    Cerchiamo di essere chiari nei commenti, altrimenti si rischia di creare inutile confusione.

    Ti pregherei di riportare ogni singolo passaggio, Come ben sai non interessa tanto il risultato finale, ma il modo con cui ci si arriva...

  7. leandro
    10/12/2023 at 11:25

    AD^2 = (1/2)^2 + (s/2)^2 = \frac{1}{4} (1+ s^{2})

     

    ma AOD è simile a AOC

    AC : 1/2 = 1/2 : AD

    da cui AD= 1 / (4 AC)

    sostituendo nell'espressione di AD

    (\frac{1}{4 AC})^2 = \frac{1}{4} (1+s^2)

    AC= \frac{1}{\sqrt{1+s^2}}

    Da cui l'area = AC  s/2 =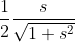 \frac{1}{2}\frac{s}{\sqrt{1+s^2}}

     

     

     

     

  8. leandro
    10/12/2023 at 11:55

     

    La so solo con la trigonometria

    detto DAE = FBE= \alpha

    DE + EF = AE sin \alpha + EB sin \alpha = (AE+EB) sin \alpha = costante er il triangolo isoscele dato.

     

     

  9. Vincenzo Zappalà
    10/12/2023 at 15:49

    caro Leandro,

    hai di nuovo sbagliato un segno...

    Hai ragione, si può fare anche senza trigonometria in un modo piuttosto semplice...

  10. Arturo Lorenzo
    10/12/2023 at 16:44

    ciao a tutti

    io utilizzo la similitudine tra triangoli.  In particolare, i triangoli APM e PBN sono simili (hanno i tre angoli omologhi congruenti) , cioè:

    x/(1-x) = PM/PN      1)

    inoltre sappiamo che PM+PN=s     2)

    da cui , mettendo a sistema la 1) e la 29, si ottiene:

    PN=(1-x)s

    PM=x s

    Da Pitagora applicato al triangolo rettangolo APM ottengo AM= x radq(1-s^2)

    Ora considero i triangoli APM e AHC. Anche questi sono simili, per cui:

    x s / h = xradq(1-s^2)/(1/2)

    da cui, esplicitando rispetto ad h, ottengo

    h=s/(2*radq(1-s^2))

    A questo punto l'area del triangolo è base per altezza /2 cioè

    Area= s / (4*radq(1-s^2))

    Da notare che nella formula dell'area compare s , non x. Cioè, qualunque posizione abbia il punto P sulla base AB del triangolo, l'area del triangolo sarà sempre la stessa (come era ovvio che fosse).

     

     

     

  11. Arturo Lorenzo
    10/12/2023 at 18:50

    Aggiungo quella che mi sembra una possibile dimostrazione semplice del fatto che la somma PM+PN nel triangolo isoscele è costante. Faccio riferimento alla figura allegata.

    Inizialmente faccio coincidere P con A. In questo caso, banalmente MP=0 e PN=s. Ora sposto il punto P lungo la base e lo pongo in P'. Chiamo M' e N' i punti sui due cateti ottenuti mandando le perpendicolari ad essi dal punto P'. Gli angoli M'P'A e N'P'B sono congruenti (perchè lo sono gli altri due angoli omologhi e la somma dei tre angoli di un triangolo è sempre pari a 180°). Ora disegno (linee tratteggiate) il triangolo simmetrico di ABC rispetto alla base AB e prolungo il segmento P'N' dalla parte di P' fino ad incontrare in M'' il lato del triangolo simmettrico. Ora, l'angolo M''P'A è congruente all'angolo BP'N' perchè opposti al vertice. Quindi, per la proprietà transitiva della congruenza, l'angolo M''P'A è congruente all'angolo M'P'A. Inoltre, l'angolo M''AP' è congruente all'angolo M'AP' per costruzione . Allora i triangoli AM'P' e AM''P' sono congruenti per il secondo teorema di congruenza. Quindi M'P' = M''P' . Ne discende M'P'+P'N'=M''P'+P'N'=AN=s (perché ANN'M'' parallelogramma) . Ciò accade per qualsiasi posizione di P sulla base AB.

    Sempre se non ho dato qualcosa per scontato.

    (scusate il foglietto di carta disegnato a mano, ma non avevo di meglio in questo momento)

  12. Andy
    11/12/2023 at 12:43

    Condivido la dimostrazione di Arturo circa la determinazione dell'area del triangolo isoscele ABC in funzione solamente di s.

    Una dimostrazione immediata circa la costanza del segmento somma s in un triangolo isoscele, potrebbe schematicamente essere la seguente:

    La somma delle perpendicolari ai lati obliqui condotte da un punto qualsiasi sulla base è sempre costante, anche quando una delle perpendicolari intercetta il prolungamento di un lato obliquo (formule in blu), ed è pari al prodotto delle misure di base × altezza / lato obliquo.

    É interessante notare che nel caso di un triangolo equilatero (che è anche un caso particolare di triangolo isoscele), la somma s è pari all'altezza del triangolo stesso (dato che b = a), che a sua volta è un caso particolare del teorema di Viviani secondo il quale:

    in un triangolo equilatero, dato un punto qualsiasi interno ad esso, la somma delle perpendicolari condotte da quel punto ai lati è pari all'altezza.

    In questo caso la terza perpendicolare è nulla.

Lascia un commento

*

:wink: :twisted: :roll: :oops: :mrgreen: :lol: :idea: :evil: :cry: :arrow: :?: :-| :-x :-o :-P :-D :-? :) :( :!: 8-O 8)

 

Questo sito usa Akismet per ridurre lo spam. Scopri come i tuoi dati vengono elaborati.