Continuo con esercizi di geometria piuttosto simpatici. In questo periodo un po' caotico non riesco a fare di più... Chi ama la geometria può trovare interessante l'ultimo commento di Andy.
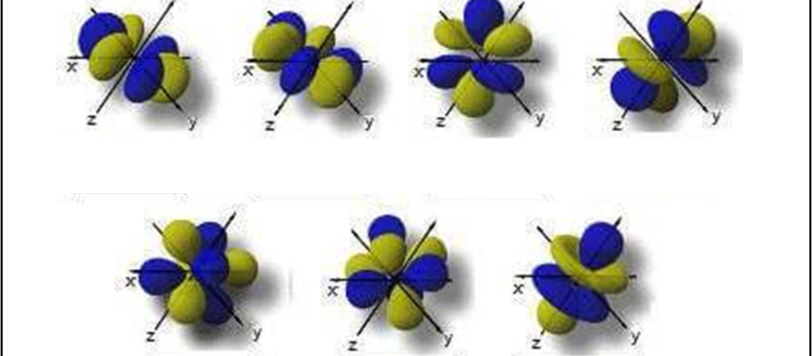
Lasciamo da parte il nucleo e spostiamoci verso l'esterno inserendo gli elettroni nei loro orbitali. In pratica, descriviamo il modello quantistico dell'atomo.
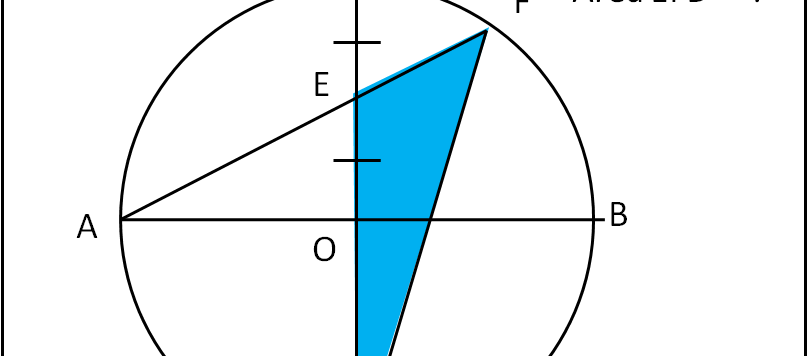
Un esercizio che poteva, come sempre, essere risolto in vari modi. Mi compiaccio con Giorgio, Andy, Giorgio, Leandro e Maurizio. Io ho voluto aggiungere un pizzico di trigonometria...
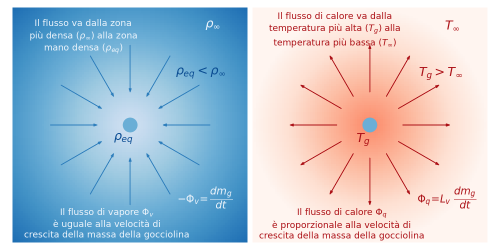
In questo articolo e nel prossimo articolo vedremo che la condensazione può far crescere le goccioline attivate fino a raggiungere la dimensioni delle goccioline nelle nuvole (r ≈10µm). Vedremo anche che la sola condensazione non può far continuare la loro crescita fino alle dimensioni delle gocce di pioggia (r ≈1mm). Cercheremo di entrare nei meccanismi del processo di crescita per mezzo della condensazione. Questo passaggio ci permetterà di farci un'idea dei tempi necessari per la crescita tramite la condensazione. Vedremo che la crescita del raggio delle goccioline rallenta all’aumentare del raggio e che l’andamento della crescita nel tempo è circa proporzionale alla radice quadrata del tempo.
Concludiamo la nostra trattazione molto semplificata introducendo i colori, gli anticolori e il meccanismo utilizzato per lo scambio di colore tra quark, quello che origina l'interazione forte. Infine viene spiegato come nessun quark può essere osservato isolato.
Un quiz sicuramente facile, almeno nella prima parte. La seconda richiede un po' d'impegno in più.
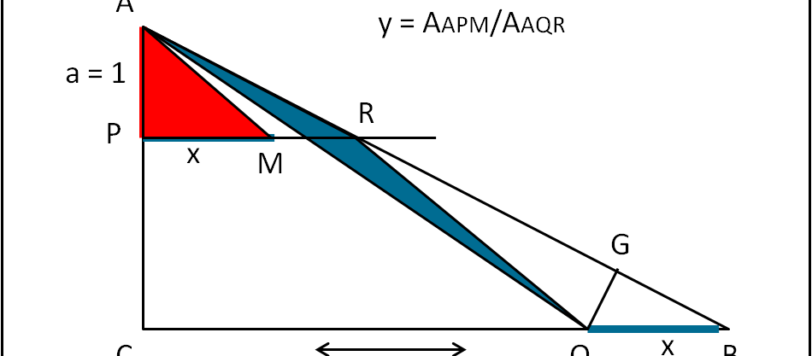
Ernesto (oltre che Andy, ovviamente) hanno risolto il quiz. Tuttavia, benché risolto in modo molto semplice si può ancora velocizzarlo. Basta ricordare che l'area di un triangolo è uguale a 1/2 del prodotto di un qualsiasi lato per la relativa altezza.
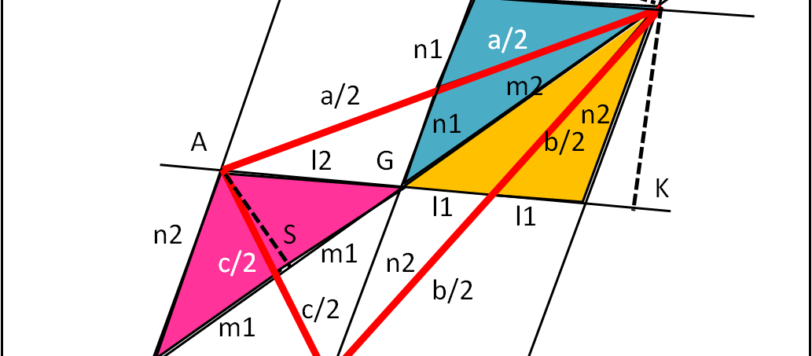
E' inutile ripeterlo: io mi diverto a inventare costruzioni geometriche e risolvere teoremi in modo non monotono e noioso. Ecco come una semplice rotazione può portare velocemente a dimostrare due teoremi relativi alle mediane di un triangolo qualsiasi.
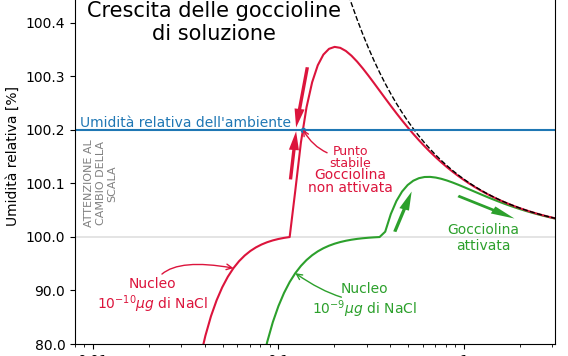
Tutti gli articoli della serie "Con la testa tra le nuvole" sono disponibili QUI Nel precedente articolo abbiamo visto che il vapore acqueo puro è molto improbabile che condensi fino a formare le goccioline contenute nelle nubi. La formazione delle goccioline è ostacolata dalla loro tensione superficiale. Le nubi comunque in natura si formano. È […]
Un quiz geometrico estremamente semplice che necessita di un minimo di ragionamento. Sia dato un triangolo rettangolo ABC, retto in C. Sul cateto AC fissiamo una lunghezza unitaria AP. Da P tracciamo la parallela a CB che incontra l'ipotenusa AB nel punto R. Consideriamo un punto Q qualsiasi sul cateto CB e sia QB = […]
Questo articolo e il successivo vorrebbero farci entrare di nascosto e in modo molto cauto nella Cromo Dinamica Quantistica (QCD), simile alla Elettro Dinamica Quantistica (QED) che studia i legami tra cariche elettriche.
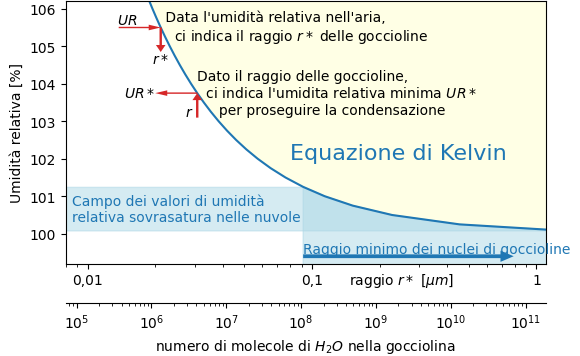
In questo articolo esamineremo il grafico della equazione che indica i valori della umidità relativa e del raggio dei punti di equilibrio (equazione di Kelvin).
Dall’esame del grafico potremo individuare dove si collocano i valori di r* per le umidità relative che si trovano usualmente nelle nuvole.
Cercheremo di farci una idea della possibilità che goccioline di acqua pura possano raggiunge un raggio superiore a questi valori di r* e quindi avere la possibilità di proseguire la loro crescita.
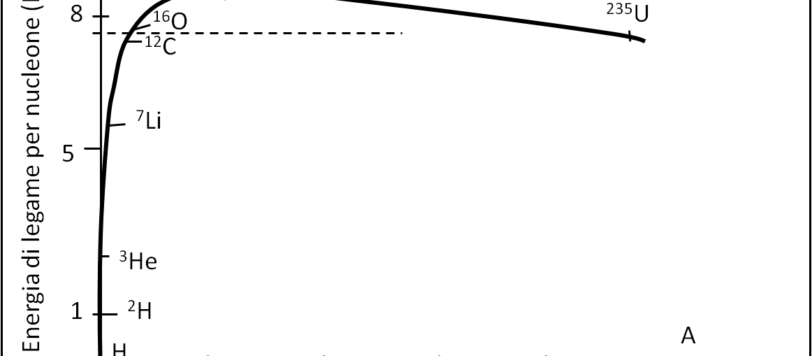
Finalmente, con grande fatica e con l'aiuto degli amici del blog, sono riuscito a completare questo breve articolo che affronta la stabilità di un legame. Vi state accorgendo che gli articoli sulla fisica nucleare appaiono un po' " a casaccio". L'idea è quella di allargarmi verso i quark e la cromodinamica quantistica. Se e quando ci riuscirò non so... ma poi penso di riordinare i vari articoli e costruirne uno che sia organizzato molto meglio. Speriamo in bene...
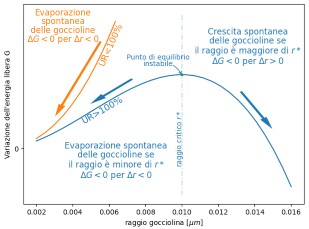
In questo articolo vedremo come cambia l’equilibrio tra vapore acqueo ed acqua liquida quando l’acqua liquida ha la forma di una gocciolina sferica.
Esamineremo il fenomeno dal un punto di vista termodinamico. Vedremo che la grandezza termodinamica che caratterizza il fenomeno è l’entropia. Vedremo anche che i fisici hanno trovato una grandezza, denominata energia libera, fortemente legata all’entropia, che in molti casi di interesse ci dice l’andamento dell’entropia. L’energia libera sarà la nostra guida per capire in quali condizioni il vapore acqueo tende a condensarsi sulla gocciolina facendola crescere e in quali condizioni la gocciolina tende ad evaporare. Queste condizioni dovranno tenere anche conto della tensione superficiale che tiene insieme la gocciolina.