Tutti gli articoli della serie "Con la testa tra le nuvole" sono disponibili QUI

Nell’articolo precedente abbiamo visto che una superficie piana di acqua pura liquida è in equilibrio dinamico con il vapore acqueo sovrastante quando la pressione (parziale) del vapore acqueo ha un particolare valore detto pressione di vapore saturo. La pressione di vapore saturo è normalmente indicata con e_s, mentre la pressione di vapore generica è normalmente indicata con e.

La pressione di vapore saturo fa da riferimento nella definizione dell’umidità relativa. L’umidità relativa è definita come rapporto tra la pressione di vapore attuale e la pressione di vapore saturo nelle stesse condizioni. L’umidità relativa è normalmente espressa in percentuale, UR=e/e_s 100%.

Quando la pressione del vapore è più bassa della pressione di vapore saturo, vale a dire quando e < e_s, cioè UR<100%, prevale l’evaporazione.

Viceversa, quando la pressione del vapore è più alta della pressione di vapore saturo, vale a dire quando e > e_s, cioè UR>100%, prevale la condensazione.

Il valore della pressione di vapore saturo dipende dalla temperatura. Più bassa è la temperatura, minore è la pressione di vapore che porta all’equilibrio tra condensazione ed evaporazione. La relazione (approssimata) che lega e_s e la temperatura è l’equazione di Clausius-Clapeyron.

A questo punto sembrerebbe possibile affermare che le nubi si formano quando una porzione d’aria umida si raffredda fino a che la sua la pressione di vapore saturo raggiunge la pressione di vapore nell’aria.

In modo equivalente sembrerebbe possibile affermare che le nubi si formano quando una porzione d’aria umida si raffredda fino a che la sua la temperatura raggiunge la sua temperatura di rugiada.

Questo può accadere quando una porzione d’aria sale e salendo si raffredda espandendosi per la minore pressione che incontra. Nell’articolo precedente abbiamo visto un diagramma “skew T -log p” che visualizza questa situazione.

La descrizione del fenomeno è sostanzialmente corretta, ma c’è un problema:
finora abbiamo considerato la condensazione del vapore acqueo su una superficie piana di acqua liquida, mentre nelle nuvole la condensazione deve avvenire su goccioline di acqua liquida approssimativamente sferiche.

Ripartiamo da questo punto.

In questo articolo vedremo come cambia l’equilibrio tra vapore acqueo ed acqua pura liquida quando l’acqua liquida ha la forma di una gocciolina sferica. Esamineremo il fenomeno dal un punto di vista termodinamico. Vedremo che la grandezza termodinamica che caratterizza il fenomeno è l’entropia. Vedremo anche che i fisici hanno trovato una grandezza, denominata energia libera, fortemente legata all’entropia. In molti casi di interesse l’energia libera è considerata di più agevole impiego per stabilire l’andamento dell’entropia. L’energia libera sarà la nostra guida per capire in quali condizioni il vapore acqueo tende a condensarsi sulla gocciolina facendola crescere o la gocciolina tende ad evaporare riducendo le sue dimensioni. Queste condizioni dovranno tenere anche conto della tensione superficiale che tiene insieme la gocciolina.

~ ~ ~ ~

Incontriamo le grandezze termodinamiche che indicano il verso spontaneo dei processi

La teoria che abbiamo finora visto vale per la condensazione che avviene su una superficie piana di acqua. Nelle nubi la condensazione invece dovrebbe avvenire su goccioline che si sono formate nell’aria a partire dall’incontro casuale di molecole d’acqua.

Quando queste goccioline crescono perché su di esse si condensa del vapore acqueo, la loro superficie esterna aumenta. Per aumentare la superficie occorre vincere la tensione superficiale. La necessità di questa energia supplementare ha effetti importanti sulla possibilità stessa che il fenomeno avvenga spontaneamente in natura.

Il secondo principio della termodinamica ci dice che sono spontanei i fenomeni per i quali aumenta l’entropia totale. Il principio parla dell’entropia totale, vale a dire che il fenomeno è spontaneo se fa crescere la somma dell’entropia del sistema con l’entropia di tutto il resto che non fa parte del sistema.

La questione è di particolare interesse in chimica per capire come evolvono le reazioni. Le quantità dei prodotti finali di una reazione dipendono proprio da dove la reazione arriva ad un equilibrio nel quale per piccole variazioni dei prodotti ottenuti l’entropia totale non varia.

In particolare sono studiati i casi nei quali la reazione avviene in ambienti che mantengono due variabili termodinamiche costanti. Ad esempio temperatura e volume costanti o temperatura e pressione costanti. La crescita della nostra gocciolina viene spesso collocata proprio in quest’ultimo caso. La trattazione è approssimata, ma porta a conclusioni che non differiscono di molto da trattazioni più complesse.

In un ambiente a pressione e temperatura costante, il fisico-chimico Willard Gibbs ha individuato una grandezza che consente di determinare il verso delle variazioni di entropia totale esaminando solo lo stato termodinamico del sistema (la nostra goccia in formazione ed il vapore circostante). Questa grandezza, che ha le dimensioni di una energia, è stata denominata energia libera di Gibbs (normalmente indicata con la lettera G).

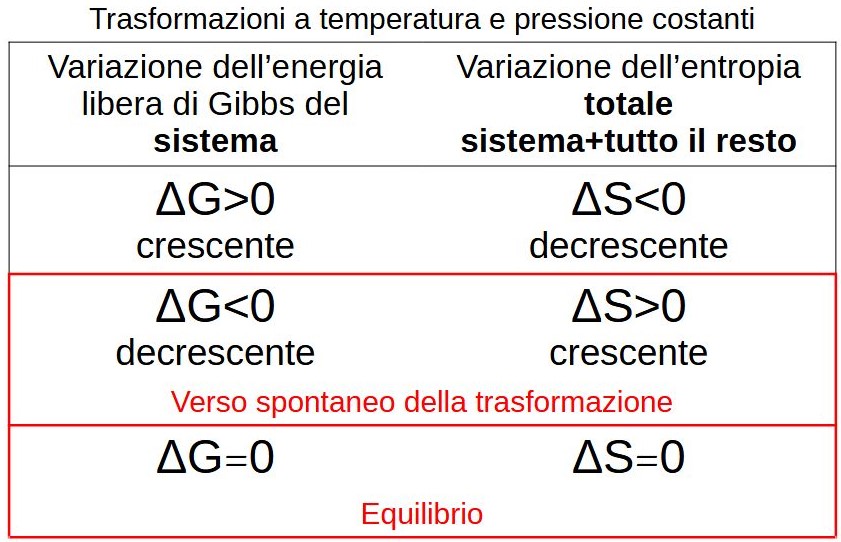
Gibbs ha dimostrato che il verso spontaneo di una trasformazione a temperatura e pressione costanti è quello con G decrescente, poiché in questo caso l’entropia totale è crescente.

Quando la trasformazione lascia invariato il valore dell’energia libera significa che la trasformazione è in equilibrio.

I testi dedicati alla fisica dell’atmosfera spesso partono direttamente da queste due ultime considerazioni. Sono partito dall’entropia poiché ho trovato interessante capire la relazione che le due affermazioni hanno con il secondo principio della termodinamica. Personalmente, mi ha chiarito il significato ed il legame con il secondo principio della termodinamica di affermazioni come: “un sistema evolve fino ad assumere la configurazione con energia minima”, che si incontrano spesso in testi di divulgazione.

~ ~ ~ ~

Applichiamo il punto di vista termodinamico alla condensazione ed evaporazione

Iniziamo ad applicare questi criteri di spontaneità e di equilibrio al processo di condensazione ed evaporazione dell’acqua. Nell’articolo precedente e nel riassunto fatto sopra l’abbiamo visto da un punto di vista prevalentemente microscopico. Riesaminiamolo da un punto di vista termodinamico utilizzando l’energia libera di Gibbs.

Per il momento trascuriamo l’effetto della tensione superficiale.

Riprendiamo la prima tabella mostrata sopra e per ciascuno dei 3 casi consideriamo come varia l’energia libera.

La nostra guida sono le due affermazioni fatte sopra:

• le trasformazioni spontanee vanno nel verso che riduce l’energia libera

• una trasformazione è in equilibrio quando l’energia libera non varia

Quando UR<100% il verso spontaneo della trasformazione è l’evaporazione.

Quindi, l’energia libera G diminuisce quando la gocciolina evapora. Considerando la nostra gocciolina sferica, possiamo affermare che, se UR<100%, G diminuisce quando il raggio della gocciolina si riduce.

Per ragioni analoghe possiamo dire che per UR>100% G diminuisce con la condensazione del vapore sulla gocciolina. Vale a dire quando il raggio della gocciolina aumenta.

Da queste considerazioni abbiamo ricavato una indicazione sulla relazione tra il raggio della gocciolina e la variazione di G dovuta alla condensazione/evaporazione.

Ora proviamo a mettere su un grafico l’andamento di questa relazione. La relazione dipende dal valore della umidità relativa e della temperatura. Quindi, fissando la temperatura, si potrebbe tracciare una curva per ciascun valore di UR.

Nella figura sotto ci sono solo due curve, una rappresentativa dell’andamento di una curva per valori di UR<100% ed una rappresentativa dell’andamento di una curva per valori di UR>100%.

Per UR<100% l’energia libera decresce con la riduzione del raggio, che equivale a dire che cresce con il crescere del raggio. Quindi la curva è crescente.

Per UR>100% l’energia libera decresce con la crescita del raggio. Quindi la curva è decrescente

Possiamo anche essere più precisi sulla forma di queste curve. La variazione dell’energia libera dovuta alla formazione di una gocciolina è proporzionale al cubo del raggio della gocciolina.

Se per UR>100% le condensazione di una gocciolina riduce G, significa che G_dopo<G_prima. La differenza tra prima e dopo è che dopo abbiamo una gocciolina di acqua liquida, prima avevamo la stessa quantità di acqua in fase vapore.
Quindi, quando UR>100%, la variazione di energia libera per la formazione di una gocciolina è ΔG=⁠ g_liquido-⁠g_vapore<0. Dove g_liquido è l’energia libera della quantità di acqua liquida nella gocciolina e g_vapore è l’energia libera della stessa quantità di acqua in fase vapore.

Se la quantità d’acqua fosse doppia avremmo che ΔG=⁠ 2(g_liquido-⁠g_vapore). Tutto questo può essere espresso dicendo che l'energia libera è una grandezza estensiva. Quindi la variazione di energia libera corrispondente alla formazione della gocciolina è proporzionale alla massa della gocciolina, la massa della gocciolina è proporzionale al suo volume, il volume della gocciolina è proporzionale al cubo del raggio. 

Quindi la curva della variazione di energia libera dovuta alla formazione della gocciolina per UR>100% è decrescente con il raggio e proporzionale al cubo del raggio della gocciolina.

Con un ragionamento analogo possiamo dire che per UR<100% la curva è crescente ed ancora proporzionale al cubo del raggio.

Evito le formule e la trattazione che permettono di calcolare i valori di G in funzione del raggio della gocciolina, mi limito a riportare il grafico.

Fin qui abbiamo considerato la sola variazione di G dovuta alla condensazione/evaporazione.

~ ~ ~ ~

Ora consideriamo anche l’effetto della tensione superficiale sull’energia libera

La crescita della gocciolina è accompagnata dalla crescita della sua superficie. Vale a dire dalla superficie che divide la fase liquida dalla fase vapore. Le molecole su questa superficie sono legate a quelle interne alla fase liquida, mentre il legame manca dalla parte della fase vapore. Questa asimmetria è all’origine della tensione superficiale che mantiene unita la gocciolina.

Nel grafico c’è l’andamento dell’energia libera dovuto alla tensione superficiale insieme a quelli dovuti alla condensazione/evaporazione.

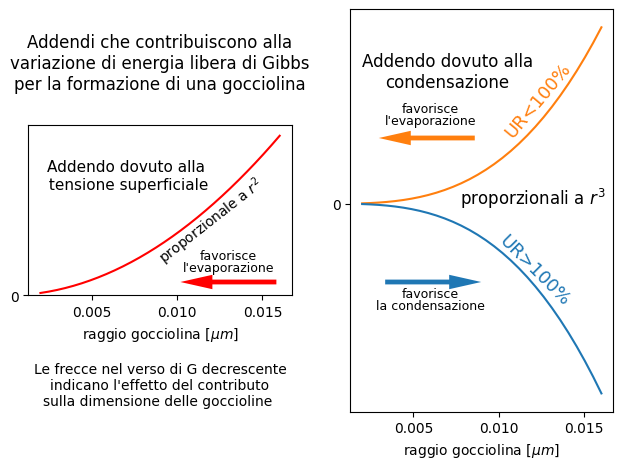
Esaminiamo qualitativamente l’addendo collegato alla tensione superficiale. La gocciolina crescendo aumenta la sua superficie esterna. Per aumentare la superficie esterna occorre fare del lavoro per vincere la tensione superficiale. Questo lavoro fa crescere l’energia libera G della gocciolina.

Questa energia libera si aggiunge a quella vista sopra per la condensazione/evaporazione. L’addendo è proporzionale alla superficie della gocciolina. Supponendo la gocciolina sferica, l’addendo sarà proporzionale al quadrato del raggio. Quindi sarà sempre positivo e crescente con le dimensioni della gocciolina.

~ ~ ~ ~

Ora dobbiamo sommare i due contributi.

Il grafico seguente ci sono le curve che otteniamo per il valore di UR<100% e per il valore di UR>100%.

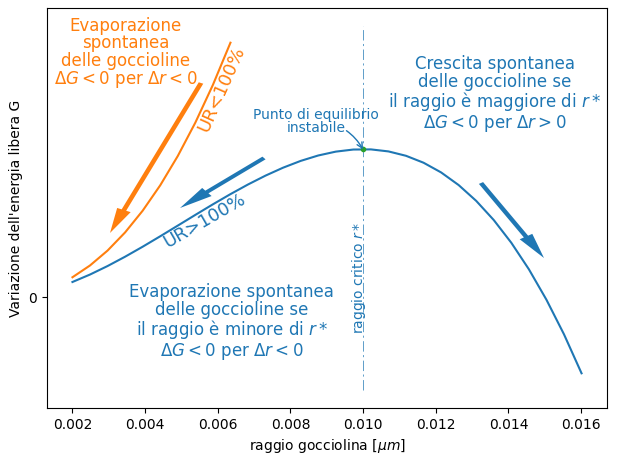
Per UR<100% sia il contributo della tensione superficiale sia il contributo della condensazione sono entrambi crescenti con il raggio. Quindi l’energia libera cresce con il raggio. Poiché le trasformazioni spontanee sono quelle con l’energia libera decrescente, le goccioline che si fossero casualmente formate in un ambiente con UR<100% sono destinate ad evaporare.

Per UR>100% il contributo della tensione superficiale, che cresce proporzionalmente al quadrato del raggio, si somma al contributo dovuto alla condensazione/evaporazione che decresce proporzionalmente al cubo del raggio.

Per goccioline piccole è preponderante l’effetto della tensione superficiale e G decresce con il decrescere del raggio, ΔG<0 per Δr<0. Poiché sono spontanei i fenomeni con G decrescente, queste goccioline tendono ad evaporare. Così si riduce il loro raggio e si riduce G.

Per goccioline grandi è preponderante l’effetto del secondo addendo e quindi G decresce con il crescere raggio, ΔG<0 per Δr>0. Il vapore nell’aria tenderebbe a condensarsi su queste goccioline. Così crescerebbe il loro raggio e si ridurrebbe G.

Tra le due zone c’è un raggio nel quale G ha un massimo. Un punto di equilibrio sebbene instabile. Questo punto di equilibrio è caratterizzabile con l’umidità relativa alla quale si riferisce la curva ed il raggio della gocciolina per il quale questo massimo si presenta. Non ho trovato una denominazione “ufficiale” per questo particolare raggio. Lo chiamo r* per comodità di esposizione.

~ ~ ~ ~

Per quanto visto in questo articolo possiamo arrivare a questa conclusione provvisoria

La crescita di una gocciolina di acqua pura può essere un fenomeno spontaneo solo un in ambiente con umidità relativa maggiore del 100% quando la gocciolina ha un raggio maggiore del raggio critico r*. Il valore di r* dipende dal valore dell’umidità relativa. In altre condizioni le goccioli di acqua pura tendono ad evaporare.

La formazione delle nuvole sembra condizionata alla possibilità che si formino goccioline di acqua con raggio maggiore del raggio critico che possano non evaporare e fare da nucleo per la condensazione di ulteriore vapore.

Nei prossimi articoli cercheremo di capire se e come questo ostacolo è superato.