Categorie: Matematica
Tags: divisione quadrato geometria quiz
Scritto da: Vincenzo Zappalà
Commenti:12
(QI) Dividiamo un quadrato in quattro parti (aggiornato) **
Consideriamo un quadrato di area A = 10.
Da un punto interno al quadrato tracciare i segmenti che lo collegano ai quattro vertici del quadrato. Essi devono dividere il quadrato in quattro triangoli, tutti diversi tra loro, ma che siano uno rettangolo e uno isoscele.
Si chiede di:
1. descrivere la costruzione dei triangoli con le caratteristiche richieste

2 Calcolare l'area dei quattro triangoli.






12 commenti
Il quadrato ABCD di area = 10 avrà un lato pari a √10. Dato che deve essere diviso in 4 triangoli (tra loro differenti) di cui uno rettangolo, inizio tracciando 2 segmenti consecutivi:
uno dal vertice A che chiamo AG di lunghezza 3 e l’altro dal vertice B che chiamo BG di lunghezza 1 sino a fare incontrare due estremi nel punto G, chiudendo il triangolo ABG.
Per il teorema di Pitagora, il triangolo ABG sarà rettangolo:^2&space;+&space;(BG)^2&space;=&space;(AB)^2) ↔
↔ 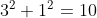
Prolungo AG sino a farlo incontrare con il lato BC nel punto H.
Il triangolo BGH è rettangolo per costruzione ed è simile al triangolo rettangolo ABG perché condividono l’angolo in H; e dato che BG/AG = 1/3, allora GH/BG = 1/3 → GH = 1/3 e quindi:
BH =^2&space;+&space;(GH)^2}) = √(1 + 1/9) = √(10/9) = √10 / 3.
= √(1 + 1/9) = √(10/9) = √10 / 3.
Successivamente da D traccio la perpendicolare al segmento AG, che incontra quest’ultimo nel punto E.
L’angolo ∠DAE = 90 – ∠GAB ; ma anche l’angolo ∠ABG = 90 – ∠GAB ,
per cui ∠DAE = ∠ABG , e quindi i due triangoli rettangoli AED e BAG sono simili;
e siccome posseggono anche uguale ipotenusa, saranno pure uguali:
DE = AG = 3 ; AE = BG = 1
Utilizzando DE come asse di simmetria, da D traccio un segmento che incontra AG nel punto F;
allora il triangolo ADF sarà isoscele, con base AF = 2×AE = 2.
Da F traccio la perpendicolare ad AB che incontra lo stesso AB nel punto L e il lato opposto DC nel punto K.
Allora il triangolo rettangolo ALF è simile ad ABG (condividono l’angolo al vertice A) per cui:
se AB/BG = √10 allora AF/FL = √10 → 2/FL = √10 → FL = 2/√10 = √10 / 5.
Ma essendo KL = BC = √10 si avrà che:
KF = KL – FL = √10 – √10 / 5 = (4/5)√10.
A questo punto, unendo F con C ottengo gli ultimi due triangoli FDC e FCH.
Conclude con il calcolo delle aree:
Area ABH = AB×BH / 2 = (√10)×(√10 / 3) / 2 = 10/6 = 5/3
Area ADF = AF×DE / 2 = 2×3 / 2 = 3
Area FDC = DC×KF / 2 = (√10)×( (4/5)√10 ) / 2 = (40/5) / 2 = 4
L’area di FCH si ottiene per differenza:
Area ABCD – (Area ABH + Area ADF + Area FDC) = 10 – (5/3 + 3 + 4) = 10 – 26/3 = 4/3
caro Andy,
tu hai fatto un caso che non corrisponde alla figura di copertina. Dovevo essere più chiaro...
I quattro triangoli devono avere un vertice in comune e gli altri due che coincidano con quelli del quadrato.
Modifico il testo per meglio chiarie la configurazione... Comunque... complimenti per l'esercizio svolto.
Caro Enzo,
ferme restando le costruzioni e le misure precedenti, aggiorno la figura, congiungendo F con B, di modo tale che F sia un vertice comune ai quattro triangoli:
Perché il punto sia interno al quadrato e non si trovi su un bordo (soluzione che non mi piacerebbe), occorre che il triangolo rettangolo abbia l'angolo retto in corrispondenza del punto interno stesso. Quindi traccio una circonderenza avente un lato del quadrato come diametro, in modo che tutti i suoi punti, se congiunti con i vertici di quel lato, producano un triangolo rettangolo. Ora devo individuare uno di questi punti che dia luogo anche ad un triangolo isoscele. La soluzione banale è scegliere il punto al centro del quadrato, così che i quattro triangoli siano uguali, e tutti sia rettangoli che isosceli. Ma questo non è divertente. Allora cerco un punto che sia distante da un vertice del quadrato quanto un lato dello stesso: quindi prendo uno dei due vertici del quadrato che non siano estremi del diametro precedente; uso questo vertice per tracciare una circonferenza con raggio pari al lato. L'intersezione fra le due circonferenze (quella non banale, non il vertice del quarato) è il punto richiesto. In questo modo, però, i triangoli isosceli sono due.
Per il calcolo dell'area, mi vedo costretto a metodi analitici, cosa che mi dà un po' fastidio...
Interessante Andy...
io ho usato un minimo di trigonometria, che sveltisce i passaggi. Comunque OK!
Forse andrebbe detto meglio come costruire il triangolo rettangolo e quello isoscele.
Aspettiamo ancora un paio di giorni e poi riporto la mia soluzione.
perfetto Giorgio.
Per il calcolo delle aree puoi usare la semplice geometria e magari un pizzico di trigonometria. Prova...
Traccio cerchio con diametro CB
Traccio cerchio centro A e raggio AB
Definisco O l'intersezione dei due cerchi
COB è rettangolo perché giace sul diametro di un cerchio
AO = AB forzano AOB ad essere isoscele.
Quindi AOB è diverso da COB.
DOC è diverso dagli altri perché
non è né rettangolo né isoscele
DOA è diverso perché, pur essendo isoscele
DO < OB essendo l'arco DO < dell'arco OB
Indicando con
L = lato/2
hi altezza relativa al triangolo Ai
A1 = L * h1
A2 = L * h2
A3= L* h3
A4= L*h4
h1+h2 = 2L
h3 + h4= 2L
A1+A2 = L*(h1+h2) = 2 L^2
A3+A4 = L*(h3+h4) = 2 L^2
Area A4 = 2 * A3 perché somma di due triangoli retangoli simili ad A3 ( ipotenuse uguale a lato).
e qui mi fermo.
correggo le aree dei triangoli
A1 = L * h1
A3 = L * h3
A2= L* h2
A4= L*h4
h1+h3 = 2L
h2 + h4= 2L
A1+A3 = L*(h1+h3) = 2 L^2
A2+A4 = L*(h2+h4) = 2 L^2
Traccio il cerchio 1, centro sul lato AB e raggio ½ √ 10 e interseco nel punto P il cerchio 2 , centro in C e raggio √ 10. APB è il triangolo rettangolo e BPC è il triangolo isoscele.
Traccio il cerchio 3, centro sul lato BC e raggio ½ √ 10 e interseco nel punto Q il cerchio 4 , centro in D e raggio √ 10.
Il triangolo BQC è identico a APB L'angolo BQC è di 90°. Anche l'angolo CQP è di 90°
CP è uguale al lato BC (raggi del cerchio 4)
Ciascuno dei due triangoli rettangoli BQC e PQC è uguale ad APB ed essi formano il triangolo isoscele BPC
i segmenti BQ , QP , AP sono uguali tra loro (doppia barretta)
posso calcolare l'area del triangolo rettangolo APB
area = ½ * AP* 2 AP = AP^2
dato che (Pitagora) AP^2 + 4 AP^2 = 10, ricavo AP^2= 2 e quindi AP = √2
Quindi il triangolo rettangolo ha area APB =2
Il triangolo isoscele BPC è composto da due triangoli rettangoli identici a APB
quindi la sua area vale il doppio di 2. Area BPC = 4
Unendo il punto P al vertice D identifico i due triangoli rettangoli APD e CPD
Questo triangolo CPD è in verità un secondo triangolo isoscele perché PC = CD.
La sua base CD vale √ 10 e la sua altezza h1 vale √ 10 meno l'altezza del
triangolo APB rispetto la sua base AB
Sappiamo che l'area di APB vale 2 quindi questa altezza vale 2 *2/ √ 10 = 4/√ 10
Allora h1 = √ 10 – 4/ √ 10
e posso calcolare l'area di CPD = (h1* √ 10) /2 = (10 – 4) /2 Area CPD= 3
resta solo da calcolare quanto vale l'area di APD
APD = area quadrato - somma aree ( APB + BPC + CPD )
area APD = 10 - 9 area APD = 1
Mamma mia, quante risposte! Sono arcicontento, ovviamente. Se riesco, oggi vi propongo la mia versione, ma vedo che tutte portano allo stesso risultato: 1, 2, 3 e 4! Questa volta ho aggiunto un pizzico di trigonometria, ma non era indispensabile...
Si può dirlo in altri termini.
ABE+DCE = 1/2 quadrato, quindi, dato che DCE=4*ABE, ABE=quadrato/10.
Perciò ABE+BEC+CEB=quadrato/10+2*quadrato/10+4*quadrato/10.
BEA= quadrato-(7/10 quadrato)= 3quadrato/10.
Da cui i quattro spicchi, sono 1,2,3,4