Tutti gli articoli della serie "Con la testa tra le nuvole" sono disponibili QUI

Nell’articolo precedente abbiamo visto che le particelle dell’aerosol atmosferico, in particolare quelle solubili in acqua, aiutano a formare i nuclei iniziali delle goccioline che formano le nuvole. Le particelle di aerosol consentono la formazione di questi embrioni di goccioline ai valori di umidità relativa normalmente presenti nelle nuvole. La crescita di alcune di queste goccioline si ferma in un punto di equilibrio. Per altre goccioline la condensazione sembra poter alimentare la loro crescita senza trovare ostacoli. Queste ultime goccioline sono dette attivate.

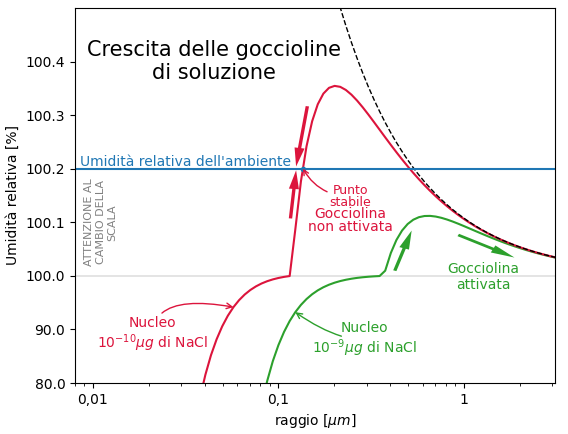
In questo articolo e nel prossimo articolo vedremo che la condensazione può far crescere le goccioline attivate fino a raggiungere la dimensioni delle goccioline nelle nuvole (r ≈10µm). Vedremo anche che la sola condensazione non può far continuare la loro crescita fino alle dimensioni delle gocce di pioggia (r ≈1mm). Cercheremo di entrare nei meccanismi del processo di crescita per mezzo della condensazione. Questo passaggio, oltre ad essere un approfondimento che mi è sembrato interessante, ci permetterà di farci un'idea dei tempi necessari per la crescita tramite la condensazione. Vedremo che la crescita del raggio delle goccioline rallenta all’aumentare del raggio e che l’andamento della crescita nel tempo è circa proporzionale alla radice quadrata del tempo.

~ ~ ~ ~

Il nostro obiettivo è capire fino a che punto la condensazione del vapore può far crescere le goccioline attivate e la velocità di questa crescita.

Una prima considerazione grossolana si basa sulla quantità di acqua (vapore e liquida) disponibile per la condensazione (oltre la saturazione) che si può trovare nelle nuvole. Un valore realistico può essere 1 grammo al metro cubo. Il numero di nuclei di condensazione adatti a formare goccioline possono essere circa 10⁹ per metro cubo. Si tratta di valori che in natura hanno una grande variabilità. Prendiamo i valori dati come possibili esempi utili per ragionare sugli ordini di grandezza.

Dai due valori dati, uniti al valore della densità dell’acqua liquida (ρ_l ≈ 1kg/lt), possiamo stimare l’ordine di grandezza del raggio medio delle goccioline supponendo che le goccioline si formino su tutti i nuclei di condensazione disponibili.

Se volete potete ricavare voi stessi il valore del raggio medio delle goccioline. Il calcolo è in appendice in fondo all’articolo.

Il raggio medio trovato (6,2 μm) è dell’ordine di grandezza del raggio delle goccioline all’interno delle nuvole (circa 10μm) ed è molto più piccolo di quello delle gocce di pioggia (circa 1mm).

Questo confronto ci fa pensare che quasi tutti i nuclei di condensazione attivati possono formare goccioline, ma solo un piccola parte si può trasformare in gocce di pioggia.

~ ~ ~ ~

Per capire meglio come avviene la crescita e farsi una idea della velocità di crescita occorre esplorare il processo che alimenta la condensazione sulle goccioline.

La spiegazione del processo di crescita delle singole goccioline per condensazione che propongo nel seguito è basata su una teoria formulata da J.C.Maxwell.

La teoria che vedremo contiene importanti approssimazioni che consentono di procedere nella trattazione. Comunque può essere utile a noi per conoscere gli elementi che influenzano la crescita delle goccioline e ai fisici per basare gli affinamenti che riducono le approssimazioni.

Devo dire che questa teoria è presentata solo nei testi più specialistici. Nei testi introduttivi sono riassunti i risultati e vengono date solo alcune indicazioni generali sul metodo utilizzato per ottenerli. A me è piaciuto molto il ragionamento seguito in questa teoria. Non è certo il lavoro più importante di J.C.Maxwell che lo ha scritto per una voce dell’Enciclopedia Britannica. Comunque è ancora molto citato. Mi è sembrato che possa farci dare uno sguardo sul modo di ragionare di un fisico del livello di J.C.Maxwell. Per questo ve la propongo in modo esteso, anche se non completo, cercando di contenere il livello di complessità. L’aspetto che mi ha colpito è la capacità di trovare la via per semplificare un problema, altrimenti praticamente irrisolvibile, con una serie di assunzioni che lo rendono gestibile ottenendo un risultato approssimato, ma comunque utile per capire il processo e basare successivi affinamenti. Queste assunzioni le troverete evidenziate nel testo che segue.

L’obiettivo della teoria è trovare la crescita nel tempo del raggio della gocciolina per effetto della condensazione sulla gocciolina del vapore acqueo circostante. Vale a dire la funzione che possiamo indicare con r_g(t) che rappresenta l’andamento del raggio della gocciolina nel tempo.

Questa funzione viene calcolata utilizzando la velocità di crescita del raggio della gocciolina dr_g/dt. A sua volta dr_g/dt è calcolata a partire dalla velocità di crescita della massa della gocciolina dm_g/dt.

Quindi la prima incognita a cui puntiamo è dm_g/dt.

La teoria di Maxwell considera due effetti prodotti dalla condensazione che accompagnano l’accrescimento della massa della gocciolina.

Il primo effetto riguarda la densità di vapore intorno alla gocciolina. La condensazione sottrae il vapore circostante la gocciolina che, trasformato in acqua liquida, accresce la massa della gocciolina. Quindi la densità del vapore nei pressi della singola gocciolina, ρ_eq, è minore della densità di vapore, ρ_∞, presente nelle zone tra le goccioline, zone dette interstiziali.

Il secondo effetto che accompagna la condensazione del vapore è il rilascio del calore latente. Il calore latente rilasciato causa un incremento della temperatura, T_g, nelle vicinanze della gocciolina. Quindi T_g sarà maggiore della temperatura delle zone interstiziali, T_∞.

La figura sottostante rappresenta una immagine qualitativa dell’andamento della densità e della temperatura attorno alla gocciolina oltre le immediate vicinanze. Il cerchietto al centro rappresenta la gocciolina, la densità del colore circostante vuole rappresentare la densità del vapore e la temperatura. Ovviamente la figura non ha nulla di realistico, tanto più che il vapore, così come ta temperatura, è sostanzialmente trasparente alla vista.

Quindi la densità del vapore cresce gradualmente allontanandosi dalla gocciolina, mentre la temperatura decresce gradualmente allontanandosi dalla gocciolina.

Concentreremo la nostra attenzione su questi “gradualmente” perché sono molto legati con la velocità di crescita della gocciolina. Cercheremo di sostituirli con una espressione più precisa.

Intanto vediamo se possiamo dire qualcosa in più sui valori della densità di vapore e della temperatura considerati sopra.

T_∞ e ρ_∞ (la temperatura e la densità di vapore dell’ambiente lontano dalla gocciolina) possiamo considerarli dati noti del problema poiché non dipendono dal processo di condensazione della singola gocciolina. La teoria assume, ragionevolmente, che T_∞ e ρ_∞ siano costanti almeno nel breve periodo di formazione della gocciolina. Da notare che, date le dimensioni della gocciolina in formazione, lontano qui significa circa ad 1mm che è 100-1000 volte il raggio della gocciolina in formazione.

Invece T_g e ρ_eq (i valori della temperatura e della densità del vapore sulla superficie della gocciolina) dipendono dal processo di condensazione e non sono noti a priori. Li dobbiamo considerare come incognite ausiliari del nostro problema che si aggiungono alla velocità di crescita della massa della gocciolina, dm_g/dt, che è l’incognita che si vuole determinare.

Però qualcosa possiamo dire su di loro. Abbiamo detto che la condensazione sottrae il vapore circostante la gocciolina. La condensazione può procedere fino a che la densità del vapore è maggiore di quella di equilibrio tra il vapore ed il liquido della gocciolina. La teoria che stiamo seguendo assume che la condensazione sia così “vorace” da portare la densità di vapore ad un valore molto vicino a questo limite. Tanto vicino da poter assumere che la densità di vapore ρ_eq sia quella di equilibrio liquido-vapore senza introdurre un errore significativo (da qui il suffisso eq).

Questa assunzione è molto importante perché lega in un modo noto, sebbene complesso i valori di T_g e ρ_eq. Nel primo articolo di questa serie abbiamo incontrato la legge di Clausius-Clapeyron che descrive la relazione tra l’umidità relativa e temperatura dei punti di equilibrio su una superficie piana di acqua pura. Nei successivi articoli abbiamo visto le correzioni da considerare quando l’acqua liquida è una gocciolina (legge di Kelvin) e quando il liquido è una soluzione (curve di Köhler). Utilizzando le proprietà dei gas, è possibile passare dall’umidità relativa alla densità del vapore. Evito di entrare nel dettaglio della relazione tra T_g e ρ_eq e nei complessi passaggi per ottenerla.

Possiamo comunque registrare che ρ_eq è legata a T_g da una funzione nota: ρ_eq=f( Tg). Questa relazione non ci dà da sola i valori di T_g e ρ_eq, ma sarà uno dei tasselli che permetterà di ricostruire il quadro completo.

~ ~ ~ ~

La crescita deve essere alimentata e la zona circostante la gocciolina deve essere raffreddata

L’effetto della condensazione sulla densità di vapore ci porta anche a pensare che ci debba essere un flusso di vapore, Φ_v, verso la gocciolina che alimenti la sua crescita. Se non ci fosse questo flusso di vapore, la gocciolina consumerebbe il vapore nelle immediate vicinanze fino a raggiungere l’umidità relativa di equilibrio liquido-vapore. A questo punto, senza il continuo apporto di vapore del flusso, cesserebbe la condensazione e la crescita.

Non meno importante è che ci sia un flusso di calore, Φ_q,dalla gocciolina e dalla sua zona circostante verso l’ambiente interstiziale. Se non ci fosse questo flusso di calore, la temperatura della gocciolina e della sua zona circostante crescerebbe fino a far cessare la condensazione.

Possiamo già mettere in relazione il flusso di vapore Φ_v ed il flusso di calore Φ_q tra loro e con la velocità di crescita della massa della gocciolina.

Faccio una premessa riguardo il verso del flusso. La convenzione è che il valore del flusso è positivo se segue quello delle coordinate. In questo caso usiamo la coordinata radiale, quindi è positivo se si allontana dalla gocciolina.

Il flusso di vapore Φ_v coincide con la velocità di crescita della massa della gocciolina a meno del segno.

Il segno meno indica che il flusso deve andare verso la gocciolina per avere una crescita della massa della gocciolina. Vale a dire che il flusso deve andare nel verso considerato negativo. Un po’ come in quei referendum dove per dire si al provvedimento occorre votare no e per dire no al provvedimento occorre votare si.

Quindi potremmo raggiungere l’obiettivo di individuare la velocità di crescita se riusciamo a determinare il valore del flusso di vapore Φ_v verso la gocciolina.

Il flusso di calore Φ_q è pari alla velocità di crescita della gocciolina moltiplicata per il calore latente specifico L_v, cioè rilasciato per unità di massa di vapore condensato.

Le due affermazioni fatte sopra credo richiedano una spiegazione.

La velocità di crescita della massa della goccioline è il rapporto tra la variazione di massa della gocciolina, dm_g, e l’intervallo di tempo, dt, nel quale è avvenuta.

Il valore del flusso di vapore Φ_v è il rapporto tra la massa di vapore che arriva o attraversa una superficie perpendicolare al flusso, nel nostro caso la superficie della gocciolina, diviso per l’intervallo di tempo trascorso. Assumendo che tutto il vapore condensi, la massa di vapore che arriva coincide con la variazione di massa della gocciolina. Quindi possiamo affermare che .

La seconda affermazione richiede un breve richiamo al significato del calore latente.

Il calore latente di evaporazione dell’acqua è il calore necessario per far evaporare l’acqua liquida. Latente perché non produce incremento di temperatura. L’evaporazione come la condensazione avvengono a temperatura costante. Quando il vapore condensa restituisce all’ambiente il calore latente assorbito nell’evaporazione in forma di calore sensibile, calore che può far incrementare la temperatura. Si può fare un parallelo con l’energia potenziale e l’energia cinetica. Il valore del calore latente di evaporazione/condensazione è normalmente riferito alla massa che lo ha prodotto. Ad esempio il calore latente dell’acqua è circa 2500 kJ/kg, che spesso viene indicato con Lv. Notate che il calore latente totale prodotto è proporzionale alla massa di acqua condensata. Ad esempio se si condensa sulla gocciolina una massa dmg=1,3 10-10 mg di vapore, il calore latente rilasciato sarà Se la condensazione è avvenuta in 1s, il flusso di calore rilasciato sarà Il calore latente di evaporazione lo sperimentiamo continuamente con la nostra termoregolazione. È possibile vederla all’opera anche con un banale esperimento. Occorre disporre di un termometro che non si gusta se esposto all’umidità, preferibilmente in grado di misurare il decimo di grado. Copritelo con un panno o una carta umida. Dopo che la temperatura si sarà assestata vedrete che la temperatura misurata è più bassa di quella dell’ambiente. La temperatura misurata in questo modo, con l’accortezza di rinnovare continuamente l’aria attorno al termometro, si chiama “temperatura di bulbo umido”. La sua differenza con la temperatura ambiente ci da una indicazione dell’umidità nell’aria. La teoria di Maxwell che stiamo utilizzando aveva lo scopo di spiegare proprio la relazione tra temperatura di bulbo umido e umidità nell’aria.

Se la velocità di crescita della massa della gocciolina è dm_g/dt, sarà rilasciato un flusso di calore Φ_q pari a L_v dm_g/dt che deve essere allontanato dalla gocciolina per non far salire la temperatura. Quindi possiamo affermare che: Φ_q = L_v dm_g/dt .

~ ~ ~ ~

Ora vediamo come questi due flussi sono generati e la loro relazione con quei due “gradualmente” detti sopra. Vale a dire con l’andamento della densità del vapore e della temperatura attorno alla gocciolina.

Il flusso di vapore ed il flusso di calore sono generati dalle differenze di densità di vapore e dalle differenze di temperatura che i due flussi tendono a compensare.

Possiamo considerare i due flussi come manifestazioni del principio di Le Châtelier: un sistema in equilibrio tende a reagire ad una perturbazione impostagli dall'esterno minimizzandone gli effetti. La perturbazione è creata dalla condensazione che sottrae vapore acqueo e fa aumentare la temperatura con il rilascio del calore latente. I due flussi tendono a ripristinare il vapore acqueo sottratto e ha ridurre la temperatura nelle vicinanza della gocciolina. Maggiore è la perturbazione, maggiore è la reazione.

In particolare, la teoria che stiamo seguendo assume che il flusso di vapore sia prodotto dalla diffusione. Vale a dire che si assume che il flusso sia causato dai moti casuali delle molecole di vapore in presenza di densità di vapore che varia nello spazio. In alcuni testi il tipo di accrescimento delle goccioline che stiamo esaminando prende il nome da questa assunzione e viene denominato per diffusione, altri testi lo chiamano per condensazione come ho fatto finora.

Il verso del flusso di vapore causato dalla diffusione va dalla zona più densa a quella mano densa. Quindi, nel nostro caso va in direzione radiale verso la gocciolina, che è proprio quello che serve.

Anche il flusso di calore, Φ_q , che nella teoria si assume dovuto alla conduzione, segue lo stesso principio. La dipendenza è con la temperatura. Il verso del flusso va dalla zona a temperatura più alta a quella più bassa. Quindi, nel nostro caso, si allontana dalla gocciolina, che è proprio quello che serve per disperdere il calore latente rilasciato dalla condensazione.

Per passare dalla descrizione qualitativa di questi due flussi ad una descrizione quantitativa dobbiamo considerare l’andamento della densità del vapore, ρ_v(r), e della temperatura, T(r), lungo gli assi radiali che hanno origine nel centro della gocciolina.

~ ~ ~ ~

Iniziamo a mettere su un grafico l’andamento della densità di vapore e della temperatura lungo uno degli assi radiali. Per la simmetria della configurazione possiamo assumere che ciò che accade su un raggio accada su tutti gli altri.

I valori ρ_eq, ρ_∞, T_g, T_∞ sono i valori agli estremi di ciascuno dei due grafici. ρ_eq e T_g sono i valori di densità e temperatura sulla superficie della gocciolina, cioè ad una distanza radiale pari al raggio della gocciolina r=r_g. ρ_∞, T_∞ sono i valori di densità e temperatura ai quali il grafico tende a raggi lontani dalla gocciolina. Matematicamente li consideriamo all’infinito.

Ora dobbiamo trovare come i due grafici raccordano questi valori. Lo faremo cercando di trovare le pendenze dei due grafici lungo un raggio.

Ad esempio, sotto c’è il grafico della densità del vapore ρ_v(r). L’andamento della parte tratteggiata che raccorda i due valori agli estremi non è noto. Cercheremo di trovarlo determinando il valore della pendenza lungo il grafico. Per pendenza intendo il rapporto tra la variazione dell’ordinata dρ_v e la relativa variazione dell’ascissa dr con dr abbastanza piccolo da confondere l’ipotenusa con la curva stessa. Matematicamente quando dr tendente a zero si ha la derivata della funzione che descrive la curva.

 

Dalla pendenza di queste curve dipendono il flusso di vapore ed il flusso di calore che abbiamo incontrato sopra. Più precisamente le grandezze che dipendono direttamente dalle pendenze delle curve sono le densità dei due flussi. Nel caso che stiamo esaminando sono il rapporto tra i flussi totali e l’area delle superfici delle sfere concentriche alla gocciolina.

La densità del flusso di vapore, che chiamo φ_v, dipende dalla pendenza della densità del vapore dρ_v /dr. Questa dipendenza è espressa da una legge nota come prima legge di Fick che rappresentiamo con l’espressione:

φ_v(r)= -D_v dρ_v /dr

Il segno meno esprime in forma matematica l’affermazione fatta sopra sul verso del flusso che va dalla zona più densa a quella meno densa.

D_v è denominato coefficiente di diffusione o diffusività del vapore nell’aria. Il suo valore di circa 2 cm²/s e dipende dalla temperatura e dalla pressione.

 

Analogamente, la densità del flusso di calore, che chiamo φ_q, dipende dalla pendenza della curva della temperatura dT/dr. L’espressione matematica di questa dipendenza è nota come legge di Fourier,:

φ_q(r)= - k_T dT /dr

k_T è la conduttività dell’aria. Vale circa 2,4 10^-2 J m^-1 s^-1 K^-1.

Ripeto le due relazioni che ci serviranno in seguito:

φ_v(r)= -D_v dρ_v /dr                           φ_q(r)= - k_T dT /dr

~ ~ ~ ~

La relazione tra il flusso totale di vapore e la densità di flusso

La teoria assume che la densità del vapore sia stazionaria. Vale a dire che i valori della densità del vapore rimangono invariati nel tempo anche se le singole molecole di vapore fluiscono continuamente verso la gocciolina. Una analogia può essere il livello dell’acqua in un fiume. Se diciamo che il livello dell’acqua è stazionario intendiamo dire che la profondità dell’acqua è costante, no che il fiume è congelato.

Da questa assunzione si ricava che il valore del flusso totale di vapore è lo stesso su qualsiasi sfera concentrica alla gocciolina.

Consideriamo la corona sferica tra qualsiasi due sfere concentriche ideali attorno alla gocciolina. Se la densità di vapore rimane invariata, significa che tanto vapore entra nella corona sferica attraversando la sfera esterna tanto vapore esce attraversando la sfera interna. Vale a dire che il flusso totale è uguale su ciascuna sfera.

Affinché il flusso totale rimanga uguale su tutte le sfere, occorre che la densità del flusso cresca mano mano che le sfere si riducono in modo che il prodotto tra densità di flusso e area della superficie della sfera rimanga costante: φ_v(r) 4 π r²= Φ_v= costante.

Quindi la densità del flusso di vapore è inversamente proporzionale al quadrato della distanza dal centro della gocciolina:

Ricordiamo anche che abbiamo visto sopra un’altra espressione di φ_v(r) :

φ_v(r)= -D_v dρ_v /dr

Da queste due relazioni otteniamo che:

In modo del tutto analogo si ottiene la relazione tra la pendenza della curva della temperatura e la densità di flusso del calore.

Quindi la pendenza della densità del flusso di vapore e la pendenza della temperatura sono inversamente proporzionali al quadrato della distanza dal centro della gocciolina.

Da notare che non possiamo trarre ulteriori informazioni da queste relazioni poiché i valori dei flussi di vapore e di calore non sono noti a priori.

~ ~ ~ ~

Abbiamo accumulato alcune informazioni sulle relazioni tra le grandezze fisiche che descrivono il processo che porta alla crescita della gocciolina.

Ciascuna delle relazioni trovate non è utilizzabile da sola per determinare i valori di queste grandezze poiché sono relazioni tra grandezze ancora incognite.

Per trovare i valori delle grandezze incognite occorre elaborare insieme queste relazioni.

Vale a dire ricavare dalle relazioni trovate, quello che in matematica è chiamato, un sistema di equazioni.

Nel prossimo articolo vedremo come sono utilizzate per trovare la velocità di crescita della gocciolina.

~ ~ ~ ~

APPENDICE

Stima del raggio medio delle goccioline che potrebbero formarsi utilizzando l’eccesso di acqua oltre la saturazione in una nuvola