Andy ha dato la risposta giusta (non c'era da dubitarne...). Io cerco, comunque, di restare ancora più  "terra-terra", dando il massimo risalto alla logica...

Disegniamo il nostro quadrato iniziale e poniamo il suo lato uguale a 1, per semplicità.

Dimostriamo innanzitutto la possibilità di dividerlo in un numero di quadrati n, che sia pari.

Purtroppo dobbiamo escludere subito la possibilità di avere n = 2. E' infatti impossibile dividere un quadrato in due quadrati.

Passiamo a n = 4. Ora tutto è più semplice: basta dividere i lati originari per 2 e, tracciando delle rette verticali e orizzontali, ottenere proprio 4 quadrati, tutti uguali tra loro, come mostra la Fig.1.

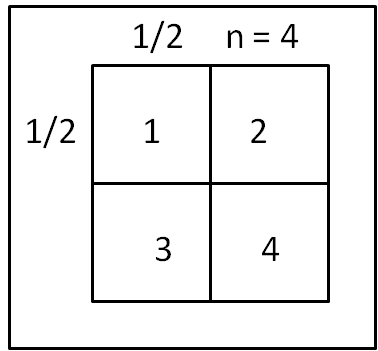
Da adesso in poi qualsiasi sia n la divisione è sempre possibile. Usiamo la seguente logica: dividere il lato iniziale in un numero di parti crescente, 1/3, 1/4, 1/5... ecc. Per 1/3 otteniamo la Fig. 2.

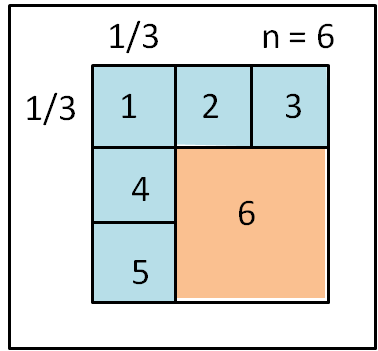
Prendiamo in considerazione la parte segnata in azzurro. Essa è, ovviamente, composta da 5 quadrati, tutti uguali tra loro, di lato 1/3. A questi 5 va aggiunta la parte rosa, che è sicuramente un quadrato avendo i lati uguali a 1 meno 1/3 . Abbiamo ottenuto una divisione in 6 quadrati di cui 5 uguali e uno più grande. Notiamo che 6 è proprio il doppio di 3.

Passiamo a n = 8. Questa volta dividiamo il lato in 4 parti e contiamo quanti sono i quadratini compresi nella parte azzurra di Fig. 3.

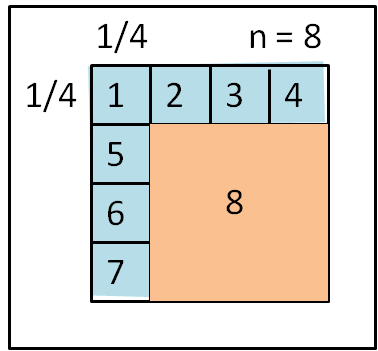
Essi sono 7. A questi aggiungiamo la parte rosa che è, ovviamente, un quadrato di lato 1- 1/4. Abbiamo ottenuto la divisione in 8 quadrati, di cui, nuovamente, 7 uguali tra loro e uno più grande. 8 è nuovamente il doppio di 4.

Senza ripeterci, possiamo continuare nella divisione del lato originario in 5, 6, 7, ecc. e ottenere, con la strategia precedente, una divisione in 10, 12, 14, ecc. quadrati. Continua, ovviamente, a valere la regola che il numero totale n di quadrati è il doppio della divisione eseguita sul lato originario.

In conclusione, abbiamo dimostrato che tutte le divisioni in un numero pari di quadrati sono sempre possibili, tranne che per n = 2.

Spostiamoci, adesso, su un numero di divisioni che sia dispari. Ovviamente 1 sola divisione ci lascia il quadrato immutato. E' possibile ottenere  n = 3 e n = 5? E' abbastanza immediato rispondere di NO. Tuttavia, occupiamoci per il momento di n = 7.  Risolviamo il problema dividendo il quadrato iniziale in 4 quadrati e segniamo in rosa il quadrato in basso a destra (uno qualsiasi andrebbe bene). Il quadrato rosa può essere considerato il quadrato originale e, di conseguenza, può essere diviso in un numero pari di quadrati. Per cui il quadrato rosa può sicuramente essere diviso in 4, 6, 8, 10 quadrati. Per completare il quadrato iniziale basta aggiungere i tre quadrati azzurri che rimangono (Fig. 4).

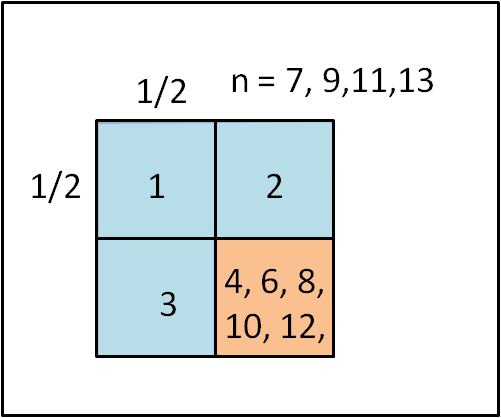
In tal modo possiamo concludere che al crescere del numero di quadrati in cui è diviso il quadrato rosa si possono sempre aggiungere 3 quadrati. Il numero di quadrati del quadrato rosa può essere 4, 6, 8, 10, ecc... e, quindi, il numero totale di quadrati è uguale a questo numero più tre, ossia 4 + 3 = 7, 6 + 3 = 9, 8 + 3 = 11, 10 + 3 =13, ecc... Possiamo concludere che tutte le divisioni in un numero dispari di quadrati è sicuramente possibile. Tuttavia, qual è il minimo numero  di quadrati ottenibile.  Per potere ottenere un numero uguale a 5, dovremmo dividere il quadrato rosa in due parti uguali che ormai sappiamo essere cosa impossibile. Il 5 quindi è un numero vietato, così come lo è, a maggior ragione, il numero 3 che vorrebbe dire far sparire nel nulla il quadrato rosa.

La risposta finale è, quindi:

La regola esiste e ci dice che è sempre possibile dividere un quadrato in n quadrati più piccoli, tranne che per n = 2, 3 e 5.