Categorie: Fisica classica Terra
Tags: Con la testa tra le nuvole processo di collisione e coalescenza velocità limite velocità terminale
Scritto da: Fabrizio
Commenti:5
Con la testa tra le nuvole - parte 6
Tutti gli articoli della serie "Con la testa tra le nuvole" sono disponibili QUI
Nell’articolo precedente abbiamo visto che il processo di diffusione/condensazione riesce a formare le goccioline all’interno delle nuvole. Lo stesso processo da solo non riesce a far crescere queste goccioline fino a farle diventare gocce di pioggia sia per il tempo che sarebbe necessario sia per la quantità di acqua liquida o potenzialmente condensabile disponibile.
| In questo articolo esploreremo un altro processo che può far crescere alcune delle goccioline fino a farle diventare gocce di pioggia. La crescita è dovuta alla collisione tra goccioline e alla successiva unione delle goccioline, detta coalescenza. La collisione tra le goccioline sarebbe rara se si muovessero alla stessa velocità. Invece, se alcune goccioline hanno una velocità maggiore di altre, queste goccioline spazzano un volume dove incontrano le goccioline più lente. Anche per questo processo cercheremo di farci una idea della possibile velocità di crescita delle goccioline/gocce. |
~ ~ ~ ~
Le goccioline d’acqua sono soggette alla forza di gravità. Galilei e Newton ci hanno insegnato che la forza di gravità produce una accelerazione che non dipende dalla massa del corpo in caduta. Per la sola forza di gravità tutte le goccioline scenderebbero a velocità crescente nello stesso modo indipendentemente dalle loro dimensioni e massa.
Ma la gravità non è la sola forza che agisce sulle goccioline. Ci sono almeno altre due forze da tenere in conto.
La gocciolina è “immersa” nell’aria. Un corpo immerso in un fluido, liquido o gas, è soggetto alla spinta di Archimede. Vale a dire una forza contraria alla forza di gravità pari al peso della massa d’aria contenuta nel volume della gocciolina. Questa forza ha spesso una grande importanza nella spiegazione dei fenomeni meteorologici. Però, in questo caso, il suo effetto è trascurabile.
La densità dell’acqua è circa 1000 volte maggiore di quella dell’aria. Di conseguenza, la spinta che l’aria produce sulla gocciolina è 1000 volte minore della forza di gravità sulla gocciolina.
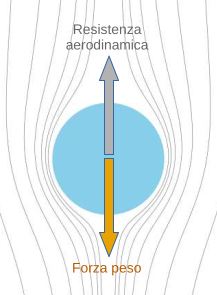
L’altra forza che agisce sulla gocciolina è la resistenza che oppone l’aria al moto della gocciolina. Quella che è chiamata resistenza aerodinamica.
Questa resistenza dipende dal raggio della gocciolina, dalla velocità della gocciolina rispetto all’aria e dalla forma della gocciolina. A parità di raggio e forma, maggiore è la velocità, maggiore è la resistenza aerodinamica.
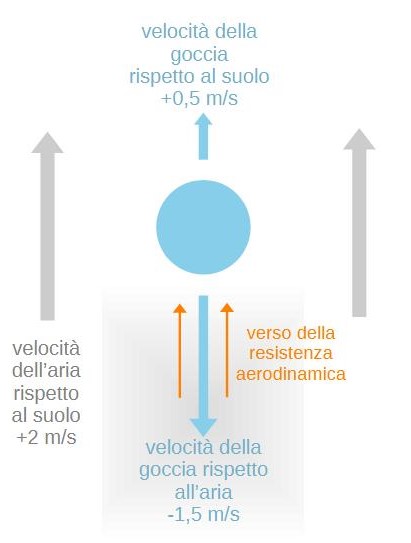
Notate che la resistenza dipende dalla velocità della gocciolina rispetto all’aria, non dalla velocità della gocciolina rispetto al suolo. Può accadere che ci sia una resistenza aerodinamica che si oppone alla forza di gravità anche quando la gocciolina sale.
Spesso le nuvole si formano in un flusso d’aria ascendente. Supponiamo che la velocità di ascesa del flusso d’aria sia +2 m/s, mentre la velocità di ascesa della gocciolina sia di +0,5 m/s. La velocità della gocciolina rispetto all’aria sarà di - 1,5 m/s. Il meno indica che la velocità relativa è diretta verso il basso. Quindi, la resistenza aerodinamica, che si oppone a questo moto relativo, sarà rivolta verso l’alto. Vale a dire sarà contraria alla forza di gravità nonostante il moto ascendente della goccia/gocciolina.
L’andamento della resistenza rispetto alla velocità relativa all’aria è molto complicato. In questo articolo Maurizio ci dà una bella descrizione dei problemi che si incontrano.
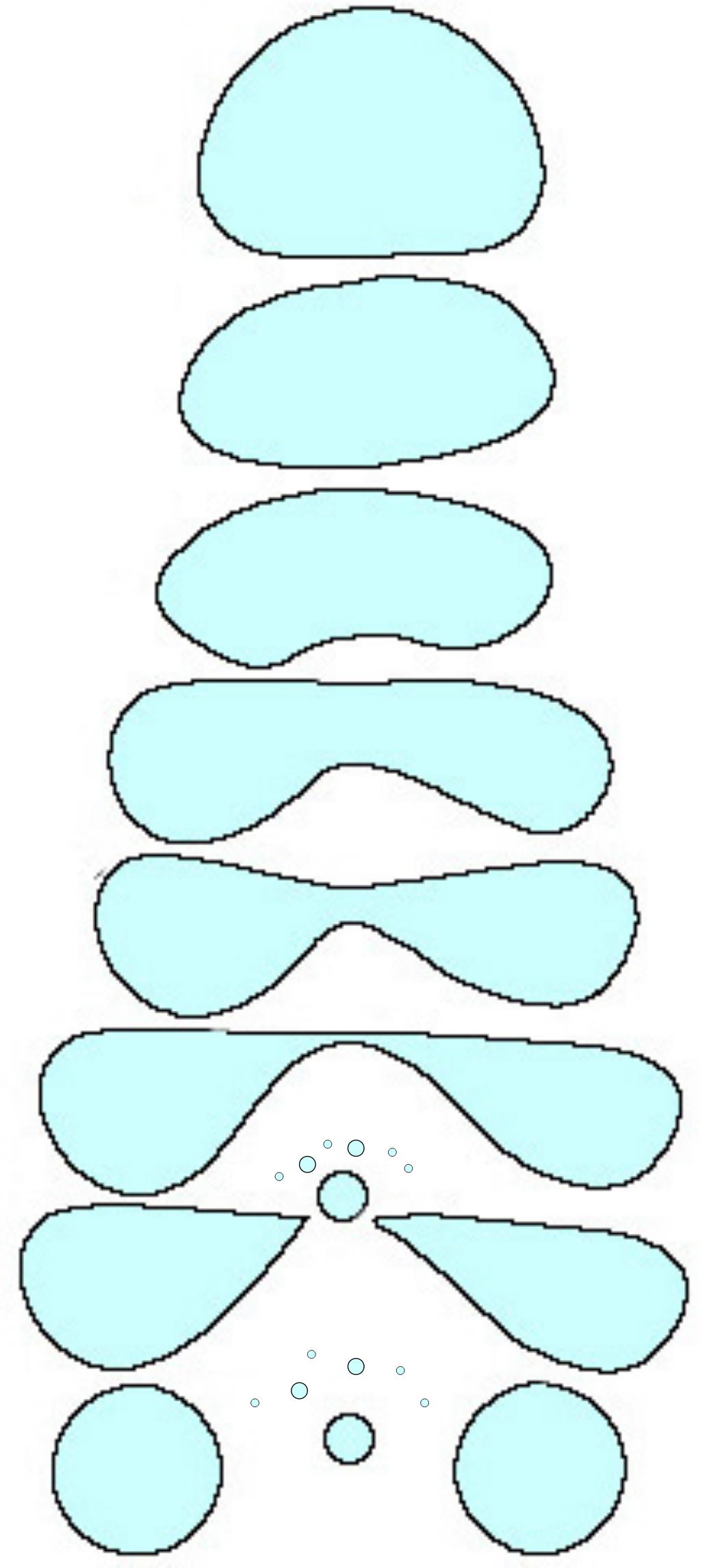
Per di più la nostra gocciolina è liquida. A differenza di un solido, nella gocciolina possono innescarsi dei moti interni dell’acqua che modificano l’interazione con il flusso d’aria circostante alla gocciolina/goccia. Inoltre le gocce più grandi cambiano forma passando da una forma sferica ad una più piatta che aumenta la resistenza aerodinamica. Possono anche innescarsi delle oscillazioni e la goccia infine può suddividersi in due o più gocce/goccioline.
La figura a fianco è una elaborazione di una immagine NASA pubblicata in un articolo divulgativo.
In realtà, la teoria non ci da una una espressione analitica completa che ci possa permettere di calcolare la resistenza aerodinamica sulla gocciolina o goccia. Quasi sempre si ricorre a relazioni empiriche o semi empiriche.
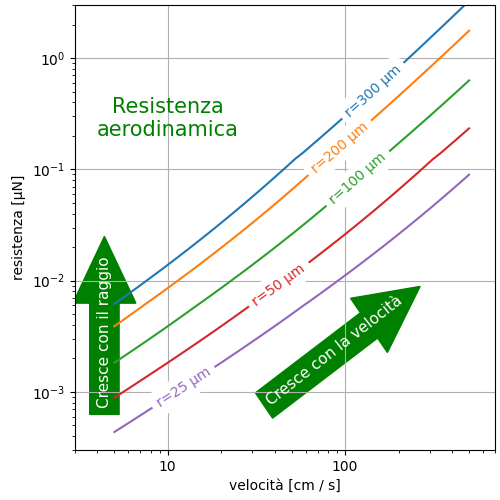
Nella figura sotto riporto un possibile andamento della relazione tra velocità della gocciolina/goccia e la resistenza aerodinamica ricavato dalla elaborazione di misure. Ciascuna delle curve si riferisce a goccioline di diverso raggio.
L’andamento di queste curve ci conferma che la resistenza cresce all’aumentare della velocità rispetto all’aria circostante e cresce all’aumentare del raggio della gocciolina.
La resistenza aerodinamica si contrappone alla forza di gravità. Quando la gocciolina ha una velocità bassa prevale la forza di gravità. Quindi la velocità della gocciolina aumenta sotto l’effetto di questa forza risultante dalla contrapposizione tra forza di gravità e resistenza aerodinamica. Parliamo sempre di velocità rispetto all’aria circostante.
La velocità aumenta fino a che la resistenza aerodinamica che produce annulla la forza di gravità. A questo punto la risultante delle forze sulla gocciolina è nulla. Quando la risultate delle forze è nulla, la gocciolina, come qualsiasi altro corpo, si muove a velocità costante. Questa velocità è chiamata velocità limite o velocità terminale. Vediamola in forma grafica nella figura sotto.
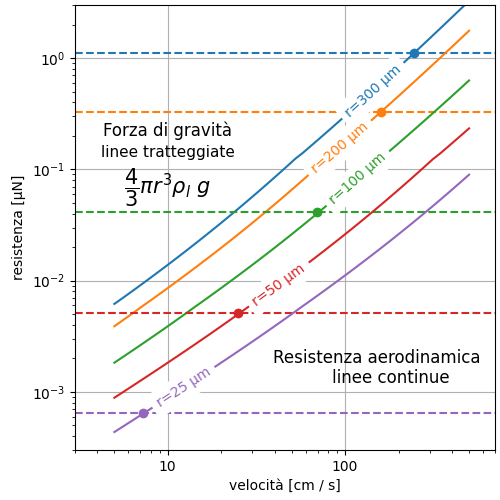
Le linee tratteggiate sono al livello della forza peso della gocciolina. La forza peso è pari al volume della gocciolina per la densità dell’acqua liquida, vale a dire la massa della gocciolina, moltiplicata per l’accelerazione di gravità. Le linee continue rappresentano la resistenza aerodinamica che cresce con la velocità e le dimensioni della gocciolina. I cerchietti colorati indicano i punti dove la resistenza aerodinamica annulla la forza peso della gocciolina.
La velocità che corrisponde a questi punti è la velocità limite o velocità terminale per goccioline/gocce di ciascuno dei raggi indicati in figura. La velocità limite è anche la velocità massima della gocciolina. Se la velocità dovesse aumentare, la resistenza aerodinamica prevarrebbe e la gocciolina/goccia sarebbe soggetta ad una forza che la rallenterebbe fino a portarla alla velocità limite. Questo articolo di Enzo tratta in modo più generale la velocità limite.
Questi cerchietti ci dicono che c’è una relazione tra le dimensioni delle goccioline/gocce e velocità limite. Questa relazione è stata molto studiata sperimentalmente. Dai risultati sperimentali sono state ricavate delle espressioni empiriche che approssimano l’andamento della relazione.
Il grafico della figura sotto è ricavato utilizzando una di queste approssimazioni.

Grafico ottenuto applicando le formule empiriche pubblicate a K.V. Beard (I976).
Le gocce/goccioline più grandi hanno una velocità limite maggiore delle goccioline più piccole.
Le goccioline all’interno delle nuvole hanno un raggio medio di circa 10µm. La velocità limite per goccioline di raggio di 10µm è circa 12 mm/s.
Per goccioline di raggio di 50µm, la velocità terminale è di circa 250 mm/s. Più di 20 volte maggiore di quella della gocciolina media.
Crescendo ancora, una goccia in formazione di 500µm di raggio ha una velocità limite di circa 4 m/s. Un velocità limite molto maggiore di quella delle goccioline.
Per quanto questi valori siano approssimati, è certo che le goccioline/gocce più grandi hanno una velocità maggiore della velocità delle goccioline più piccole. Per velocità intendo sempre la velocità delle gocce/goccioline rispetto all’aria.
Quindi le goccioline/gocce più grandi possono crescere inglobando le goccioline più piccole che incontrano nel loro percorso.
~ ~ ~ ~
Proviamo a vedere la massa delle goccioline che si trovano sul percorso della goccia più grande in un intervallo di tempo che indico con il simbolo Δt.

Partiamo dalla massa di acqua liquida contenuta nelle goccioline presenti in un certo volume all’interno di una nuvola. Il rapporto tra questa massa ed il volume che la contiene la chiamo ωL. Valori che si trovano nelle nuvole sono di qualche grammo per metro cubo.
Proviamo a vedere quanta di questa massa si trova sul percorso di una goccia. Per semplificare il discorso supponiamo che:
-
le goccioline sul percorso della goccia siano tutte della stesso raggio;
-
i percorsi della goccia e delle goccioline siano rettilinei e paralleli;
-
la velocità rispetto all’aria della goccia v(rG) e della gocciolina v(rP) abbiano il valore delle loro velocità limite. Il contenuto delle parentesi ci ricorda che la velocità limite dipende dal raggio della gocciolina.
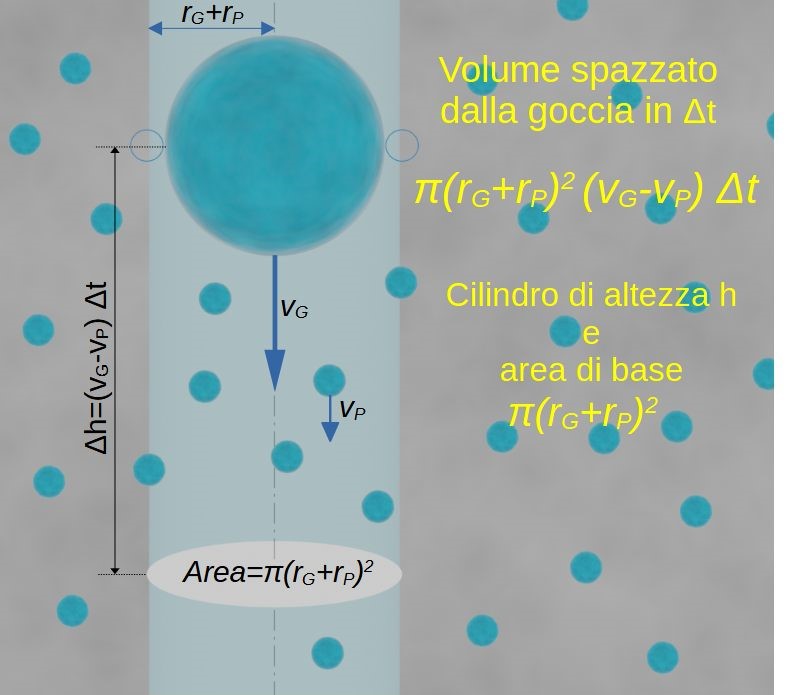
Le goccioline raggiungibili dalla goccia sono quelle che si trovano, almeno in parte, all’interno di un cilindro di raggio rG+rP. Vale a dire le goccioline che distano dal percorso della goccia meno della somma del raggio della goccia (rG) con il raggio della gocciolina più piccola (rP). La posizione delle gocce/goccioline la identifico con il loro centro.
Quindi l’area della base del nostro cilindro è π(rG+rP)2.
Ora cerchiamo di trovare l’altezza del cilindro che contiene le goccioline che sono raggiungibili dalla goccia nell’intervallo di tempo Δt.
La goccia ‘insegue’ le goccioline alla sua velocità limite v(rG) Le goccioline “scappano” alla loro velocità limite v(rP). Quindi l’altezza che cerchiamo sarà ( v(rG) - v(rP)) Δt.
Il volume che contiene le goccioline raggiungibili nell’intervallo di tempo Δt è:
π(rG+rP)2 (v(rG) – v(rP)) Δt
Per ottenere la massa delle goccioline raggiungibili nell’intervallo di tempo Δt occorre moltiplicare questo volume per ωL vista sopra.
ωL π(rG+rP)2 (v(rG) – v(rP)) Δt
Non tutte le goccioline che si trovano in questo volume spazzato collidono con la goccia più grande.
 All’avvicinarsi della goccia più grande, la traiettoria delle goccioline è deviata dallo spostamento dell’aria che fa posto alla goccia. La maggior parte delle goccioline più piccole evita l’impatto con la goccia più grande poiché seguono le linee di flusso d’aria.
All’avvicinarsi della goccia più grande, la traiettoria delle goccioline è deviata dallo spostamento dell’aria che fa posto alla goccia. La maggior parte delle goccioline più piccole evita l’impatto con la goccia più grande poiché seguono le linee di flusso d’aria.
Le goccioline un poco più grandi, per la maggiore inerzia, non seguono le linee di flusso dell’aria. Sono comunque deviate dalla traiettoria rettilinea ed in parte evitano la goccia.
 Inoltre, non tutte le goccioline che collidono sono catturate dalla goccia più grande.
Inoltre, non tutte le goccioline che collidono sono catturate dalla goccia più grande.
In alcune situazione, tra le due gocce si forma un cuscinetto d’aria che le fa “rimbalzare”. Questo effetto è considerato meno rilevante del precedente, almeno per la maggior parte delle collisioni tra gocce e goccioline nelle nuvole.
Per tenere conto della differenza tra le goccioline catturate e quelle presenti nel volume visto sopra viene introdotto un fattore che rappresenta l’efficienza della cattura. Questo fattore è normalmente indicato con E(rG,rP). Per quanto detto sopra, il valore di questo fattore dipende sia dal raggio della goccia grande sia dal raggio della gocciolina piccola.
Come esempio, nel grafico riporto i valori della efficienza di cattura di goccioline di 10µm di raggio, rP = 10µm, ricavati da dati sperimentali
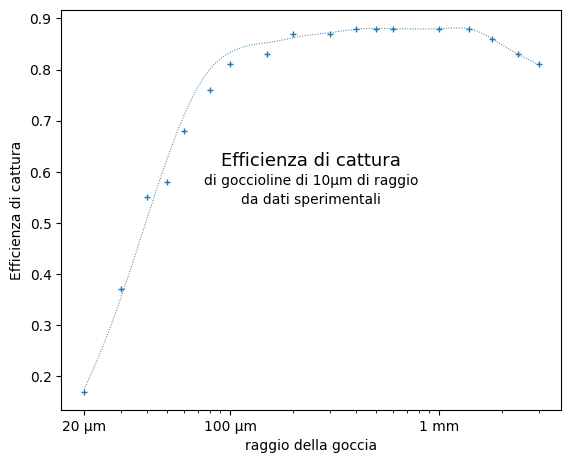
Grafico basato su dati pubblicati dai fisici Klett e Davis (1973), Beard e Ochs (1984) e Mason (I971).
La crescita della massa della goccia sarà pari alla massa dell’acqua liquida contenuta nel volume spazzato dalla goccia ridotta dalla efficienza di cattura.
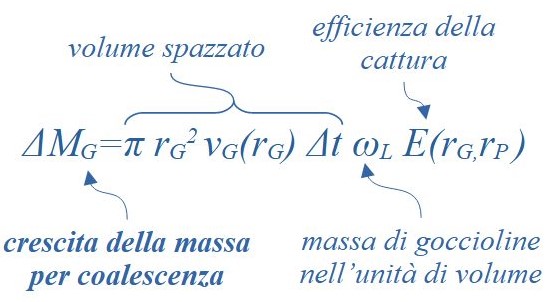

Questa espressione riporta in modo sintetico le considerazione fatte finora. Si tratta di una equazione differenziale poiché mette in relazione il tasso di crescita di rG (a sinistra) con una funzione della stessa variabile (a destra).
Risolvendo questa equazione si può ottenere come cresce il raggio della goccia nel tempo, rG(t).
La soluzione analitica di questa equazione è complicata dalla presenza delle due funzione v(rG) ed E(rG,rP) difficili da esprimere e da trattare analiticamente. Abbiamo visto sopra i loro grafici. Inoltre nella equazione appare anche il raggio rP delle goccioline che vengono catturate.
Per semplificare la trattazione abbiamo assunto che le goccioline siano tutte dello stesso raggio. Prendo il valore di rP = 10µm.
In appendice c'è una soluzione analitica della equazione basata su una approssimazione molto drastica delle funzioni v(rG) ed E(rG,rP). Qui proseguiamo in base ai dati empirici visti sopra.
Per valutare l’espressione della velocità di crescita del raggio si possono stimare i valori di v(rP), v(rG) e E(rG,rP) dai loro due grafici e inserire i valori trovati nella espressione della velocità di crescita del raggio della goccia. Nel riquadro seguente c’è un esempio.

Il grafico sottostante riporta i valori calcolati della velocità di crescita della goccia ottenuti ripetendo il calcolo per un numero sufficiente di valori di rG a partire da rG=20µm, cioè da una gocciolina che in partenza ha un raggio doppio delle altre.
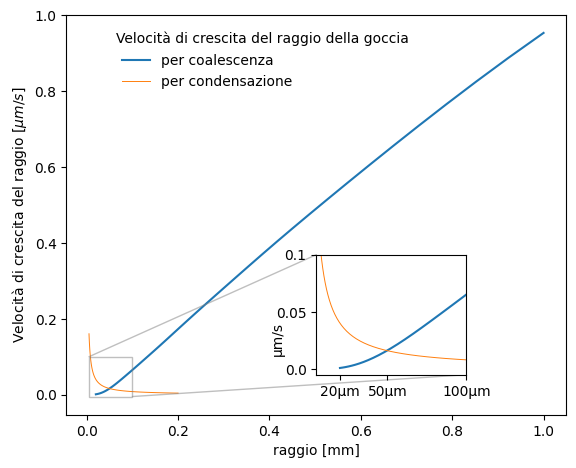
Nel grafico ho inserito anche la velocità di crescita del raggio per condensazione che abbiamo esaminato nell’articolo precedente.
La velocità di crescita del raggio per coalescenza aumenta con il raggio, mentre quella per la sola condensazione si riduce progressivamente. Nell’esempio in figura, diventa prevalente la crescita per coalescenza per un raggio della goccia di circa 50µm.
Per una velocità di crescita che continua ad aumentare con la crescita del raggio, come quella nella figura sopra, corrisponde una crescita che è vicina ad una crescita esponenziale.
Qui sotto riporto un grafico che vuole rappresentare un possibile esempio di crescita di una gocciolina/goccia nel tempo.
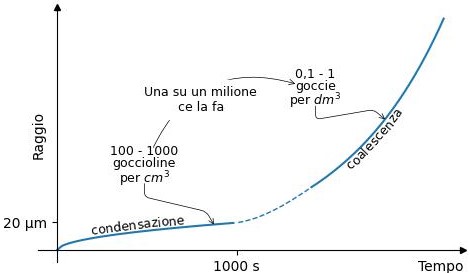
La parte sinistra della curva rappresenta la crescita per condensazione, quella vista nell’articolo precedente. La parte a destra rappresenta la crescita per coalescenza.
La crescita per condensazione porta le goccioline fino ad raggio di circa 10-20µm. I valori di raggio più elevati si trovano nelle nuvole marittime dove ci sono meno nuclei di condensazione. L’andamento della crescita per condensazione è proporzionale alla radice quadrata del tempo. Quindi la velocità di crescita rallenta al crescere della gocciolina.
La crescita per coalescenza ha un andamento di tipo esponenziale che continua a crescere con il raggio.
Il numero di goccioline che si trovano nella prima parte della curva è tra cento e mille per centimetro cubo (tra 102 e 103 cm-3 ). Di queste goccioline solo una su un milione riesce a “saltare” sulla parte destra della curva (0,1 – 1 dm-3 ).
L’avvio di una significativa crescita per coalescenza di una gocciolina richiede che la gocciolina “fortunata” abbia raggiunto una dimensione ampiamente superiore a quella delle altre goccioline in modo che la sua velocità limite permetta di raggiungerle.
Il meccanismo con il quale le goccioline “fortunate” riescono a crescere più delle altre è ancora oggetto di ricerca. Ci sono alcune ipotesi considerate plausibili. Alcune sono basate sulla non uniformità delle condizioni all’interno della nuvola e sulla natura statistica dei fenomeni. Condizioni locali favorevoli alla crescita per condensazione o collisioni statisticamente possibili, ma fuori dalla media, possono produrre la differenziazione nelle dimensioni delle goccioline necessaria per innescare il processo di collisione-coalescenza.
~ ~ ~ ~
Ascesa e caduta delle gocce
Un altro aspetto interessante è vedere quando un goccia può diventare pioggia, cioè scendere fino ad arrivare al suolo. Per esplorare questo aspetto mi baso su una teoria pubblicata dal fisico E. G. Bowen. (1950).
Finora abbiamo considerato la velocità della goccia e delle goccioline rispetto all’aria circostante. Per stabilire se una goccia sale o scende dobbiamo passare a considerare la velocità della goccia rispetto al suolo.
Spesso le nuvole si formano in un flusso d’aria ascendente. Normalmente è proprio l’ascesa della messa d’aria a creare le condizioni di umidità relativa che consentono la condensazione delle goccioline. Indichiamo con w la velocità ascensionale di questa massa d’aria rispetto al suolo e indichiamo con u(rG) la velocità della goccia rispetto alla suolo. La velocità della goccia rispetto alla suolo è il rapporto tra la variazione di quota della goccia ed il tempo impiegato: dzG/dt.
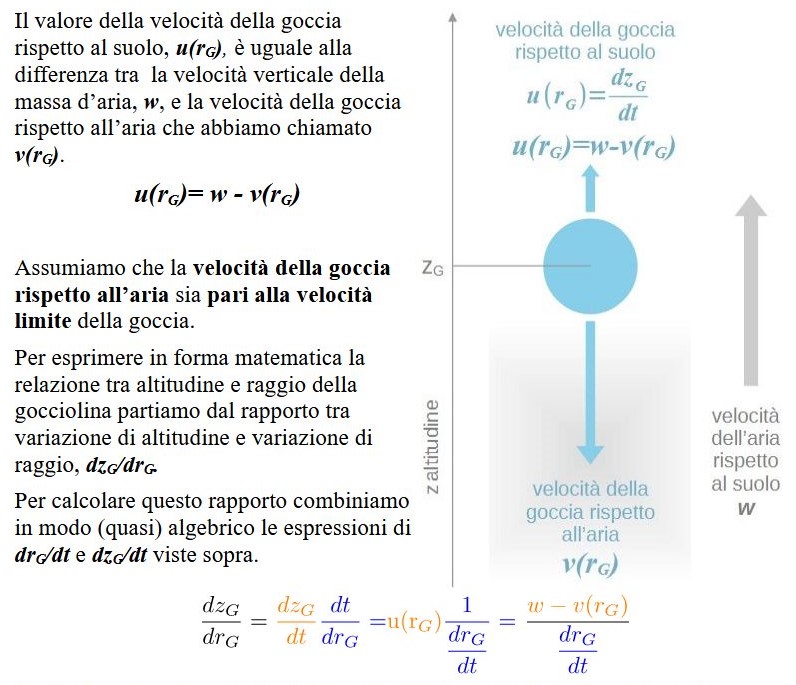
In questa espressione ha un ruolo importante la velocità ascensionale della massa d’aria. Il numeratore è positivo fino a che la sua velocità limite è minore della velocità rispetto al suolo della massa d’aria. Vale a dire che la goccia sale sospinta dalla massa d’aria che la contiene fino a che è abbastanza piccola da avere una velocità limite minore della velocità della massa d’aria.
Quando la goccia è ancora piccola, drG/dt è anche esso piccolo, come possiamo vedere alcune figure sopra nel grafico della velocità di crescita. Poiché drG/dt è a denominatore, il rapporto dzG/drG tenderà ad essere grande. Vale a dire che piccole variazioni del raggio corrispondono a una salita relativamente grande.
Quando la velocità limite della goccia supererà la velocità ascensionale della massa d’aria, la goccia inizierà a scendere. Nella discesa continuerà a cresce catturando le goccioline che incontra fino a che sarà all’interno della nuvola. Superata la base della nuvola, non trovando più goccioline, cesserà la crescita.
La sua discesa continuerà fino al suolo se le sue dimensioni e la sua velocità sono abbastanza grandi da non farla evaporare totalmente lungo il percorso.
Nel grafico qui sotto ci sono alcune curve che rappresentano l’andamento dell’altitudine della gocciolina rispetto al suo raggio per diverse velocità ascensionali della massa d’aria che le contiene.
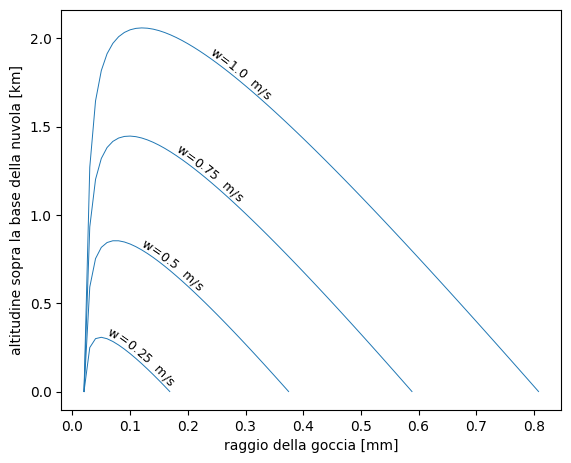
Grafico ottenuto dai dati dei grafici precedenti elaborati secondo il modello di E. G. Bowen. (1950)
La teoria che porta ha queste curve è molto semplificata. I valori che si ottengono sono solo indicativi. L’andamento delle curve è comunque di questo tipo anche in teorie più raffinate e più vicine ai valori misurati. In particolare rimane la forte dipendenza del raggio delle gocce e della stessa formazione della pioggia dalla velocità ascensionale della massa d’aria.
Nell’ultimo grafico è apparso in modo esplicito il ruolo della velocità ascensionale della massa d’aria nella crescita che porta le goccioline alle dimensioni delle gocce di pioggia. L’ascesa della massa d’aria ha un ruolo spesso essenziale anche nelle fasi precedenti. La massa d’aria ascendendo si espande. L’espansione causa la diminuzione della temperatura che innalza l’umidità relativa e la porta oltre la saturazione. In questo modo si creano le condizioni per la formazione delle goccioline che abbiamo visto negli articoli precedenti.
In questa serie di articoli ho provato a raccontare la microfisica dei processi che portano alla formazione delle goccioline nelle nuvole e la loro crescita fino a diventare gocce di pioggia. Per affrontare i fenomeni che portano all’ascesa di masse d’aria occorre passare ad una visione dei fenomeni su scala più ampia dai chilometri alle migliaia di chilometri. La lascio per una futura serie di articoli mia o di altri che si vorranno cimentare.
Nel racconto che ho fatto non ho considerato la possibilità che si formino cristalli di ghiaccio all’interno della nuvola. Mi sono limitato a descrivere quelle che sono denominate nuvole calde. I fenomeni che avvengono nelle nuvole fredde, dove si formano anche cristalli di ghiaccio, sono in parte simili a quelli che abbiamo visto. Aumenta notevolmente la varietà dei modi nei quali può avvenire la formazione e la crescita dei cristalli sia dalla fase liquida dell’acqua sia dalla fase vapore.







5 commenti
A parte che come dici ci si basa su valori molto approssimati, credo ci sia un banale errore di calcolo nel riquadro della velocità di crescita della goccia:
drG/dt per rG=100 = 1/4 . 10^-6 . 1,21^2 . 238 . 0,83 per cui il risultato sarebbe = 7,21 . 10^-5 mm/s
Comunque nel grafico che rappresenta l’andamento dell’altitudine della gocciolina rispetto al suo raggio per diverse velocità ascensionali della massa d’aria che le contiene, vale la pena di ricordare ai "profani" che rappresenta condizioni "delicate". In un cumulonembo (torri di nuvole dei temporali, tipo panna montata) si arriva anche a 15 m/s, cioè in essi l'aria sale (e più in là scende) fino a una decina di chilometri di altezza in una decina di minuti, a circa 40 Km/h. Molti anni fa ho visto un aliante che ci volava sotto venire letteralmente risucchiato da un cumulo per uscirci poi con le ali spezzate e il pilota con il paracadute.
Con queste velocità i chicchi di grandine ti possono ridurre in un colabrodo, motivo per cui gli aeroplani evitano assolutamente di entrarci, assistiti dai radar meteorologici che ne segnalano i nuclei.
A Vicenza, sempre molti anni fa, avevo invece un amico coraggioso che veniva pagato per seminare le nubi con lo ioduro d'argento nella speranza che piovesse anziché grandinare. Lui si portava sul fronte del temporale e lì, mentre disperdeva il prodotto, riduceva al minimo il motore e si lasciava trasportare dal vento come una foglia. Alla fine ne usciva in picchiata e veniva ad atterrare prima che fosse troppo tardi per evitare il pericolo dello wind shear (cambio improvviso di direzione del vento). Quest'ultimo è un fenomeno per il quale ancora oggi non ci sono molti rimedi, si cerca solo di prevederlo ed è tanto più pericoloso per gli aerei a getto, ma il discorso qui si fa lungo.
Conto comunque su un tuo impegno a proseguire questi interessantissimi studi, io intanto mi accingo a leggere l'appendice. Ti confermo che in questi giorni ho affrontato di petto anche l'amico Schroedinger, prima con le chiare lezioni di Vincenzo, ma poi (perché la fame vien mangiando) anche arrivando all'equazione di d'Alambert e l'operatore di Hamilton. E, dai... mi avete reso soddisfatto di me stesso :-)
ps. non farmi diventar matto scrivendo Il numero di goccioline che si trovano nella prima parte della curva è tra cento e mille per centimetro cubo (tra 102 e 103 cm-3). Di queste goccioline solo una su un milione riesce a “saltare” sulla parte destra della curva (0,1 – 1 dm-3 ). Ho potuto dare un sospiro di sollievo solo consultando il grafico subito sopra.
Alberto, grazie per la segnalazione dell'errore di calcolo e per l'incoraggiamento a proseguire.
Non avevo effettuato il quadrato del rapporto tra i raggi. Il risultato che ho ottenuto è circa 6 10^-5 mm/s. Credo che il tuo risultato più alto sia dovuto al fatto che hai elevato alla 4a il rapporto. Fammi sapere se convergiamo sul 6 10^-5 mm/s ho sto facendo ancora qualche errore.
Grazie per le informazioni pratiche sulle velocità ascensionali. Il grafico a velocità ascensionali molto più elevate sarebbe fuorviante poiché risulterebbero gocce molto più grandi che in realtà si andrebbero a frazionare, oltre agli altri fenomeni che segnali che non ho affrontato.
Sono contento della tua soddisfazione per i risultato che hai raggiunto con Schroedinger e dintorni. Il problema (o la fortuna) è che dopo la soddisfazione di avere aperto una porta si scopre che oltre ce ne sono altre e torna la curiosità e la voglia di provare ad aprire anche quelle. Mi sembra che anche tu ti sei avviato su questa strada.
Sì, 1,21 non va ulteriormente elevato al quadrato, per cui 5,97.10^-5 mm/s è il risultato corretto.
Per esempio non ci hai ancora parlato della nebbia
che anche questa mattina mi perseguita con i suoi 6°C e umidità al 99%, visto che il punto di rugiada (dew point, point de rosée) è calcolato a 5,9°C. Qui la massa d'aria è praticamente immobile, ben schiacciata dall'alta pressione a 1025 hPa. Goccioline così piccole che apparentemente sembrano non rispettare neppure la forza di gravità. La terra però è bagnata e... anche la superficie della Laguna ;-)
E penso al vecchio in Amarcord, circondato dalla nebbia, che si guarda attorno e dice: "Se questa l'è la morte, l'è 'na gran bruta roba!"
So benissimo che si tratta di foto molto disprezzate dai soloni dell'arte fotografica, ma di fronte a queste luci sospese tra acqua e cielo non riuscirò mai a trattenermi. Sono foto che ho scattato nel corso delle mie gite su e giù per la Laguna di Venezia, quasi sempre con i miei smartphone Huawei LYA-L29 (Leica) oppure Oppo Find X5 Pro (Hasselblad). Naturalmente, Fabrizio, mentre nei giorni scorsi montavo questo slideshow, non potevo che pennsare alle tue lezioni.
https://www.youtube.com/watch?v=joGsad2PSD0
E già che ci sono ti mostro anche il video che ho girato durante la "buriana" che ha fatto subito seguito a tale annuvolamento:
https://youtu.be/-vZZc7PsYx8
Alberto, hai colto un bel campione di nubi e di fenomeni meteo come la sequenza della tromba d'aria con il suo dissolvimento. Mi piacerebbe poter capire le cause fisiche che hanno portato a questi tipi di nuvolosità e di fenomeni. Purtroppo non sono (ancora) in grado di farlo. L'argomento comunque è molto interessante.
Sarà che non frequento saloni d'arte fotografica, ma alcune immagini mi sembra facciano anche un bel effetto estetico.