Ovviamente, Andy ha colpito ancora ... Ormai i problemi geometrici sono un discorso limitato a noi due. Fabrizio dice di non essere forte in geometria (ma non sembra proprio). Per accontentarlo, la prossima volta passerò a un quiz di fisica classica.

Permettetemi una piccola riflessione... E' molto utile imparare i concetti classici e, spesso, banali di geometria (ma anche di fisica), ma, se non si cerca di utilizzarli in casi pratici, rimangono nozioni molto vaghe e non mettono in moto le capacità di logica e razionalità. Io continuerò a proporli, sperando che altri lettori riescano a fare questo passo fondamentale per capire realmente il significato geometrico e fisico di un problema.

Riporto di seguito una soluzione al quiz leggermente diversa da quella di Andy, anche se rimane veramente un esercizio estremamente facile, alla portata di chiunque conosca le principali caratteristiche delle figure geometriche. Caratteristiche che sono state spiegate e rispiegate nelle pagine di questo Circolo.

Consideriamo la Fig. 1, dividendo il rettangolo in quattro parti.

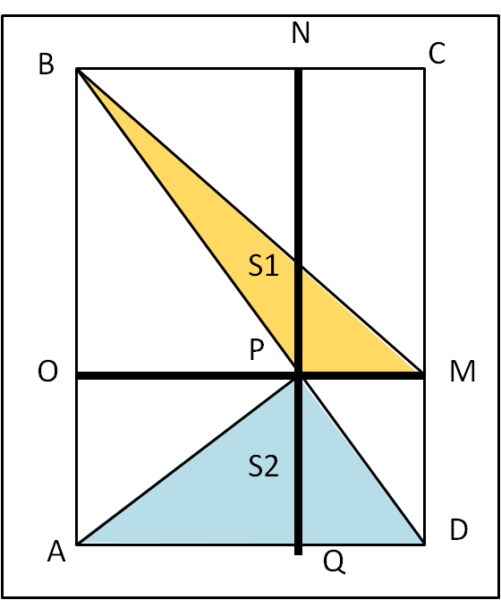
Calcoliamo l'area del rettangolo come somma delle aree dei quattro rettangoli in cui è stato diviso. Ricordiamo che l'area del triangolo arancione è S1 e quella del triangolo azzurro è S2.

Evidenziamo subito i due rettangoli contornati dalle linee rosse di Fig. 2

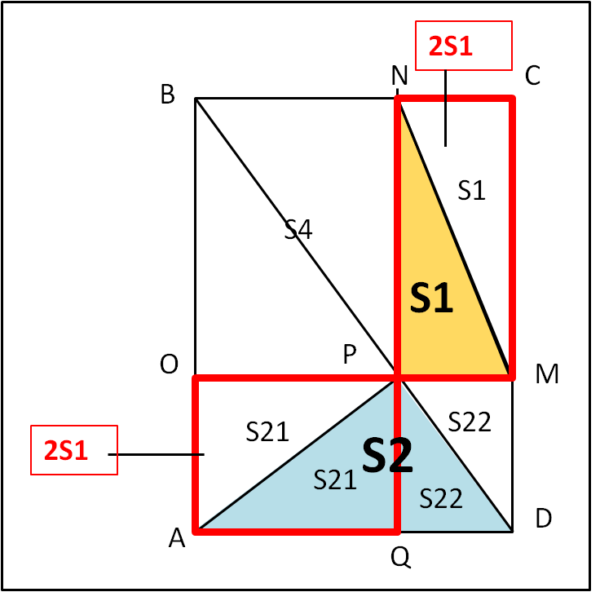
Avendo stessa base e stessa altezza l'area del triangolo arancione iniziale è anche uguale a quella disegnata in Fig. 2. Ne segue che il rettangolo in alto a destra ha area 2S1.

Sappiamo che la diagonale divide il rettangolo in due parti uguali, per cui:

S_BDA = S_BCD

Le due aree possono essere scritte come:

S4/2 + 2S21 + S22 = S4/2 + 2S1 +S22

Ne segue che:

2S21 = 2S1

Il rettangolo in basso a sinistra ha area uguale a quello in alto a destra, come indica la figura.

Passiamo alla Fig. 3, dove è contornato in azzurro il rettangolo (2S22) in basso a destra.

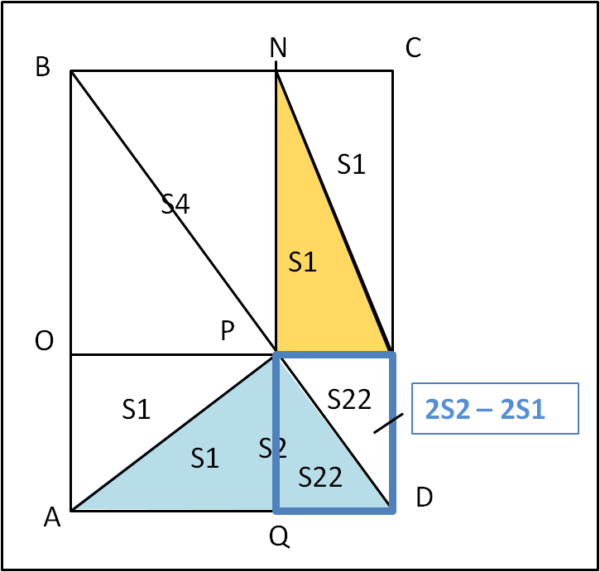
Possiamo scrivere:

2S1 + 2S22 = 2S2

ossia:

2S22 = 2S2 - 2S1

Concludiamo con la Fig. 4, dove S4 (in alto a sinistra) viene evidenziato dal contorno verde.

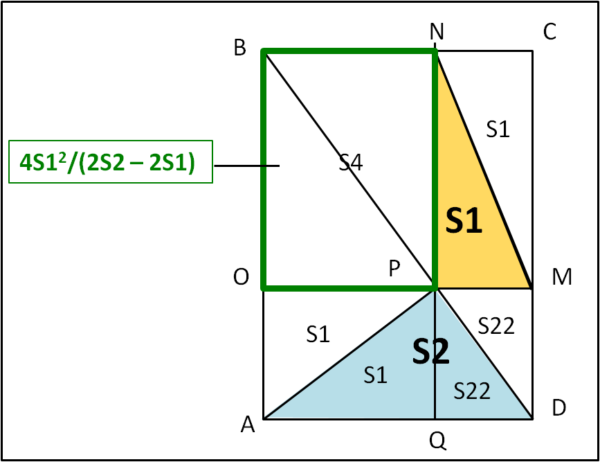
Possiamo scrivere:

NP = 2S1/PM

OP = 2S1/PQ

Moltiplicando le due relazioni:

NP OP = S4 = 4S1²/(PM PQ)

S4 = 4S1²/(2S2 - 2S1)

Non ci resta, adesso, che sommare le aree dei quattro rettangoli:

Stot = S4 + (2S2 - 2S1) + 4S1 = 4S1²/(2S2 - 2S1) + 2S2 - 2S1 + 4S1 = 4S1²/(2S2 - 2S1)+ 2S1 + 2S2

che con banali passaggi porta a:

Stot = 2S2²/(S2 – S1)

Tutti calcoli che si possono fare veramente "a mente" ...