Il baricentro di una "falce"(con soluzione)**
Le mie speranze di vedervi partecipanti attivi dei quiz proposti, soprattutto quando si parla di meccanica, si sono spente. Ho pensato, allora, di modificare leggermente questo tipo di presentazione. Innanzitutto, oltre al quiz, darò, fin dall'inizio, anche la risposta finale, in modo che venga superata la paura di riportare un risultato non corretto. Lascerò il quiz irrisolto per un paio di giorni e poi aggiungerò all'articolo la soluzione, descritta passo dopo passo, in modo che vengano digeriti e messi in pratica concetti che abbiamo descritto esaurientemente nel Circolo. Chissà che non si sollevi un po' più d'interesse... Ricordiamoci che per comprendere appieno le meraviglie dell'Universo è fondamentale capire molto bene i concetti base della meccanica classica: è inutile parlare di relatività e meccanica quantistica se le basi della fisica restano ancora un piccolo mistero e un ostacolo troppo arduo...
Problema sul baricentro di un disco sottile
Ad un disco sottile omogeneo (di densità costante) di raggio r viene tolta una parte circolare di raggio r/2, tangente internamente al disco originale.
Determinare le coordinate del baricentro della figura così ottenuta.

Il problema sarà risolto con due metodi: il primo attraverso la definizione stessa di baricentro, il secondo con l'utilizzo dei momenti delle forze.
Risposta (OG = 5r/6)
SOLUZIONE
Primo metodo
Descriviamo il primo metodo cercando di essere divulgativi al massimo. Il tutto potrebbe essere ottenuto in modo ben più rapido…
Ricordiamo la formula fondamentale che ci regala le coordinate del baricentro di un sistema di masse mi rispetto a un punto qualsiasi O.
d = ∫di mi/∫mi
dove di sono i vettori che uniscono il punto O con i baricentri delle singole masse.
La comparsa del segno di integrale non deve spaventare, dato che esso rappresenta solo una somma. Nel caso particolare dell’esercizio che andiamo a svolgere le masse in gioco sono soltanto tre: la massa della falce (mf), la massa del cerchio grande di raggio r (mg) e quella del cerchio piccolo di raggio r/2 (mp).
Ovviamente, tenendo conto che la massa è uguale al volume moltiplicato per la densità (che è la stessa in tutti i casi), si ottengono i seguenti valori:
mg = π ρ r2
mp = π ρ r2/4
Avendo a che fare con figure bidimensionali (ossia con spessore z uguale a zero) i volumi si riducono a essere delle aree. Le masse sono, perciò, le aree moltiplicate per la densità della lastra sottile, che continuiamo a chiamare ρ.
La massa della falce non è altri che la differenza tra la massa del cerchio grande, considerato pieno, meno la massa del cerchio piccolo, anch’esso considerato pieno:
mf = mg – mp = π ρ r2 - π ρ r2/4 = π ρ r2 (1 – ¼) = ¾ π ρ r2
A questo punto, data la simmetria della figura, possiamo fare a meno di considerare i vettori di e limitarci a una sola componente, quella che unisce i centri dei due cerchi, che sono per definizione complanari. Chiamiamo x questo asse e scegliamo come punto da cui calcolare le distanze dei baricentri il punto O, dove l’asse x incontra il cerchio grande. Le coordinate y e z sono, ovviamente, nulle, data la forma della figura, per cui xf, xg e xp sono le coordinate dei tre baricentri.

Scriviamo la (1) considerando il baricentro del cerchio grande (xg) in funzione del baricentro della falce (xf) e del cerchio piccolo (xp) Notiamo anche che la somma della massa della falce e quella del cerchio piccolo è uguale alla massa del cerchio grande:
xg = (xf mf + xp mp)/(mf + mp) = (xf mf + xp mp)/mg
A noi, però, interessa calcolare xf, conoscendo già xg e xp. Possiamo scrivere:
xg mg = xf mf + xp mp
xf mf = xg mg - xp mp …. (2)
Inseriamo le masse calcolate precedentemente:
xf(¾ π ρ r2) = xg π ρ r2 - xp π ρ r2/4
Tutti termini contengono un fattore comune (π ρ r2) che può essere semplificato. Risulta perciò:
¾ xf = xg – xp/4
Al posto di xg e xp, scriviamo le distanze dei baricentri dei due cerchi rispetto a punto O.
xg = r
xp = r + r/2 = 3/2 r
Da cui, sostituendo:
¾ xf = r – 3/8 r
xf = r (1 – 3/8)/(3/4)
xf = r (5/8)/(3/4) = r(5/8 ∙ 4/3)
xf = 5/6 r
Notiamo che la (2) dice praticamente che possiamo scrivere la (1) anche nel caso in cui si devono sottrarre delle masse: basta considerare queste masse NEGATIVE.
Secondo metodo
Il secondo metodo comporta lo stesso tipo di calcolo, ma utilizza i momenti delle forze agenti sulla nostra figura, assumendo che essa possa ruotare attorno all’asse passante per O e perpendicolare al piano della falce. Le forze in gioco sono tre: la forza di gravità del cerchio grande (Fg), quella del cerchio piccolo (Fp) e quella della falce (Ff). Dato che il cerchio piccolo è vuoto esso subisce una forza uguale e contraria alla forza di gravità che avrebbe qualora fosse pieno. Il momento di tale forza ha segno opposto a quello del cerchio grande considerato pieno. Siamo di fronte alla figura che segue

e, per l’equilibrio della falce, dobbiamo imporre l’uguaglianza dei momenti, ossia:
Mf = Mg – Mp
I momenti delle forze sono uguali a:
M = x m
Per cui:
xf Ff = xg Fg – xpFp
Le tre forze di gravità sono uguali alle masse moltiplicate per l’accelerazione di gravità g
xf mf g = xg mg g – xp mp g
semplificando la g, otteniamo:
xf mf = xg mg - xp mp
che è proprio la (2) del metodo precedente. Da qui in poi i calcoli si svolgono nello stesso modo…






6 commenti
Considerando O l'origine dell' asse orizzontale, si considera la massa del disco pieno positiva e centrata in r, mentre la massa del disco piccolo , si considera negativa e centrata in 3/4 r .
Massa pieno * braccio pieno =
Massa vuoto * braccio vuoto=


Massa totale = Massa pieno - Massa vuoto =
Quindi la posizione del centro di massa , per definizione è:
Massa pieno * braccio pieno - Massa vuoto * braccio vuoto
------------------
Massa totale
La posizione del centro di massa sull ' asse orizzontale sarà quindi
--------------------------------- =
il braccio della massa vuota è 3/2r
quindi lo sviluppo corretto è
da cui
ecco anche la mia soluzione (primo metodo):
Il baricentro del disco intero si trova al centro del disco per la simmetria dell'oggetto.
Considero il disco intero composto di due corpi: il disco con il buco di massa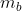 ed il riempimento del buco di massa
ed il riempimento del buco di massa  .
.
Il baricentro del disco con il buco si trova sul suo asse di simmetria ad una distanza incognita (x) dal centro del disco dove sappiamo si trova il baricentro del disco intero. La distanza x dovrà essere tale da posizionare il baricentro del disco intero, considerato composto dai due corpi, al centro del disco.
poiché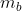 è proporzionale a
è proporzionale a =\frac{3}{4}&space;\,&space;r^2) e
e  è proporzionale a
è proporzionale a 
Peró, peró, da qualche parte dovresti spiegare ai più profani che πr^2 è un'area e non un volume, quando dici:
tenendo conto che la massa è uguale al volume moltiplicato per la densità (che è la stessa in tutti i casi), si ottengono i seguenti valori:
mg = π ρ r2
mp = π ρ r2/4
(a parte il fatto che g e p che sarebbero pedici)
caro Albertone...
come il volume diventi una superficie e una superficie una linea l'abbiamo discusso parlando di momenti d'inerzia. Mi sembrava, comunque, una ovvietà. In fondo, anche un disco sottile ha una massa...
Mi piacerebbe che tu partecipassi più attivamente ai quiz o sono troppo facili?