Come tagliare le unghie a una tigre … ***
Guardando un documentario sulle tigre e sui suoi “artigli”, ho pensato che per limitare la sua pericolosità si potrebbero tagliarle le … unghie. Non avendo a disposizione una tigre ho dovuto limitare tale approccio a un felino di dimensioni minori. Perché non utilizzare un gatto? A casa mia ve ne sono molti e avrei potuto approfittarne… E’ bastata, però, una loro occhiata per farmi capire che era un’operazione che non desideravano affatto e che sarebbe stata del tutto inutile oltre che dolorosa, sia per loro che per le mie mani.
Come spesso è capitato in ambito scientifico ho perciò desistito dall’esperimento pratico e mi sono concentrato su un esperimento teorico.
Descrivo il procedimento usato per costruire geometricamente l’artiglio
Cominciamo con la Fig. 1a.
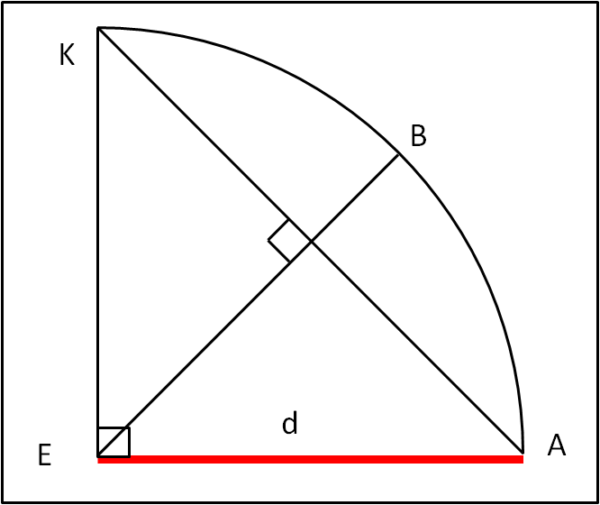
Consideriamo un segmento EA di lunghezza d (qualsiasi). Tracciamo la perpendicolare EK. Con centro in E descriviamo la circonferenza di raggio EA fino a incontrare la perpendicolare in K. Uniamo K con A e determiniamo il punto di mezzo B dell'arco KA. Uniamo E con B, ottenendo il triangolo curvilineo EBA.
Proseguiamo con la Fig. 1b.

Scegliamo un punto a piacere su EB, ad esempio P. Da P tracciamo la perpendicolare ad EB. Con centro in P e raggio PE descriviamo il tratto di circonferenza ED.
Passiamo alla Fig. 1c.
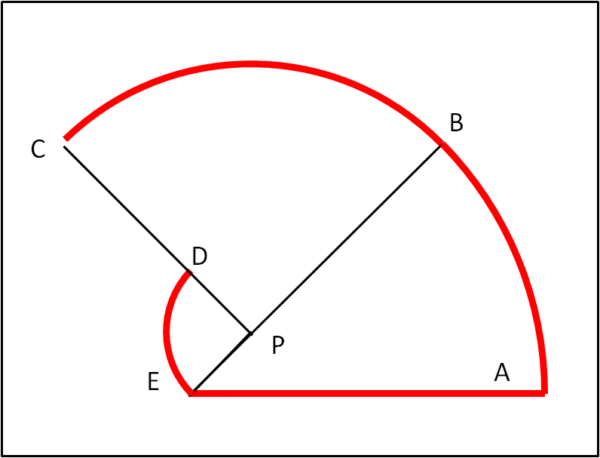
Con centro in P e raggio PB tracciamo la relativa circonferenza fino a incontrare la retta ED in C.
Concludiamo con la Fig. 1d.
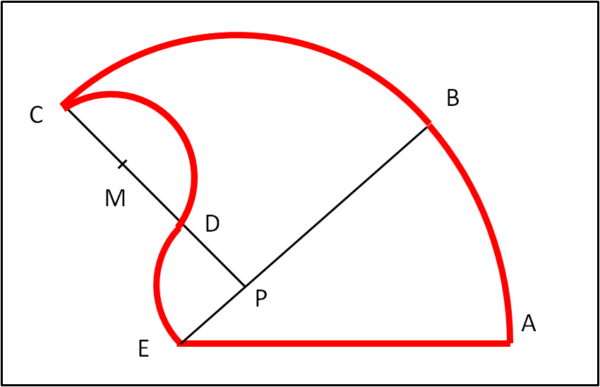
Determiniamo il punto medio M del segmento CD e tracciamo la semicirconferenza di centro M e raggio MC.
Possiamo tranquillamente cancellare le linee di costruzione ed ecco l’artiglio “teorico” rappresentato in Fig. 2.
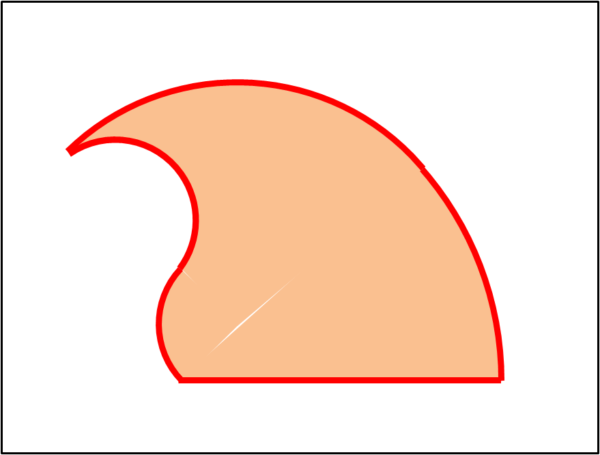
Bene, adesso tocca a voi.
L’esperimento consiste nel dividere esattamente in due parti uguali l’area dell’artiglio di Fig. 2, con il minor numero possibile di operazioni, eseguibili, sempre, con la riga non graduata e il compasso molle.
P.S.: Per operazione si intende l'azione svolta con la riga e/o il compasso.
A coloro che daranno la migliore risposta prometto di fornirgli una tigre (mansueta) per passare all’esperimento pratico!






5 commenti
Caro Enzo,
se non ho mal interpretato tutta la costruzione "dell'artiglio" e se i il metodo ed i calcoli sono corretti, sostituendo con lettere le misure dei segmenti, ottengo la seguente figura (sperando che non faccia cattiva....figura!):
Ovvero per qualunque 0 < e < d/2 , l’area sopra la bisettrice EB equivale all’area sotto la stessa.
Quindi l’operazione da compiere è tracciare la bisettrice dell’angolo retto AEK (fattibile con compasso e righello non graduato).
No, Andy... come al solito non fai una brutta "figura", anzi...
L'unica cosa che mi sembra inutile è il limite posto a "e". Può benissimo essere uguale a zero o superare d/2 e diventare uguale a d. Ovviamente, si trasforma un po' l'artiglio e/o si ribalta... non ti sembra?
Praticamente, ormai, questi quiz "geometrici" sono diventati una discussione tra te e me... Ma va benissimo così...
La geometria è fondamentale, come dimostrano i brocosomi delle cicaline!
E' vero Enzo,
ho posto il limite affinché si possa ottenere una forma canonica di artiglio e per non avere una tigre con le unghia.....rifatte!
Tanto per confermarti che seguo i tuoi quiz (seduto in divano), posso dirti che leggendo la soluzione di Andy mi sono subito chiesto perché quella limitazione di e, poi leggendo il tuo commento mi sono subito accorto che hai scritto e/2 invece di d/2
per Andy
per Albertone
mi fido, mi fido...