Una celebre giostra ci regala un semplice, ma istruttivo, esercizio di dinamica. Chi vuole cimentarsi può fermarsi dopo la presentazione del problema e proseguire da solo.

La giostra in cui vi sono seggiolini che ruotano a grande velocità è un vero "classico". E più la giostra ruota velocemente e più i seggiolini tendono ad alzarsi rispetto al suolo. Vediamo di porci un problema riguardo ad essa...

La giostra è formata da un palo che porta sulla cima un disco di raggio r che ruota solidamente col palo. Al posto del seggiolino mettiamo una certa massa M che è attaccata al disco con una fune di lunghezza d. La Fig. 1 mostra uno schema della giostra.

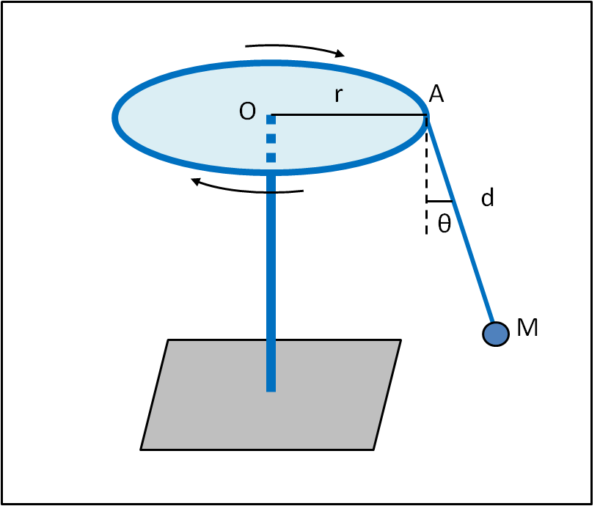
Come si può notare la fune è inclinata di un angolo θ rispetto al palo. Come già detto questo angolo è legato alla velocità di rotazione. Ci chiediamo, perciò, qual è il periodo di rotazione P della giostra affinché la massa M mantenga questo angolo rispetto al palo verticale.

Chi vuole cimentarsi nell'esercizio può fermarsi qui e proseguire da solo...

Risolviamo il problema in due sistemi di riferimento: quello di chi guarda il tutto dall'esterno e quello della massa M che ruota. Il primo è un sistema inerziale, il secondo no. Il risultato, però, DEVE essere lo stesso.

Sistema inerziale

Ridisegniamo, in Fig. 2, la giostra, inserendo le forze a cui è soggetta la massa M rotante, che possiamo identificare come un punto M (il baricentro in cui è racchiusa tutta la massa). Essa subisce, ovviamente, la forza peso F_p ma, nel contempo, anche la tensione F_t della corda nel punto A, che la tiene legata al disco. I versi delle due forze sono quelli indicati.

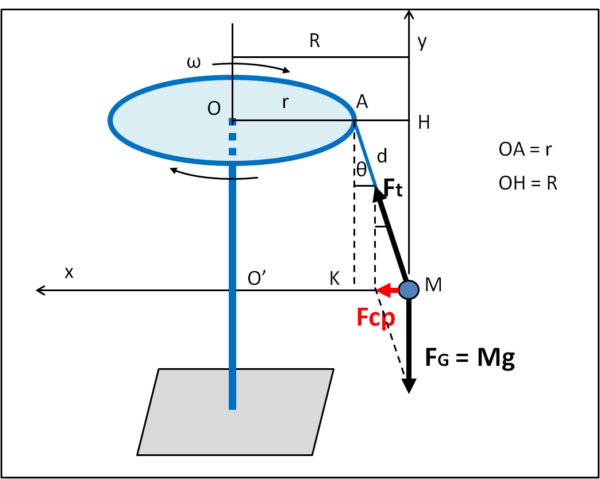
Sommando le due forze otteniamo la forza che regola la rotazione di M attorno al palo ed essa non è altro che la forza centripeta F_cp.

F_cp = F_p + F_t

Questa forza è diretta verso il palo perpendicolarmente ad esso. Introduciamo gli assi x e y, con origine nel punto M. Possiamo, perciò, passare ai moduli delle componenti delle  forze.

La componente di F_cp secondo y deve essere nulla, ossia:

F_t cos θ =  F_p  = M g              .... (1)

Dove g è l'accelerazione di gravità.

La componente di F_cp secondo x (l'unica sua componente) risulta essere

F_cp = F_t sin θ

F_t = F_cp/sin θ = M a_cp /sin θ          ....(2)

dove a_cp è l'accelerazione centripeta

Inserendo la (2) nella (1), abbiamo:

M cos θ a_cp/sin θ =  M g

a_cp = g (sin θ/cos θ)

a_cp = g tan θ     .... (3)

A questo punto ricordiamoci della formula che ci regala l'accelerazione centripeta nel moto circolare uniforme:

a_cp = ω² R

Nel nostro caso

R = r + d sin θ

a_cp = ω² (r + d sin θ)

Ma la velocità angolare ω è data da:

ω = 2π/P

a_cp = (2π/P)² (r + d sin θ)

Ricordando la (3), abbiamo:

g tan θ   = (2π/P)² (r + d sin θ)

P² = (2π)² (r + d sin θ)/(g tan θ)

P = 2π √((r + d sin θ)/(g tan θ))

Sistema non inerziale

Immaginiamo di vedere il tutto stando al posto della massa M. Ovviamente, lei si sente ferma per cui la somma di tutte le forze agenti su M deve essere uguale a zero. Riproponiamo la Fig. 3 con le nuove forze agenti su M.

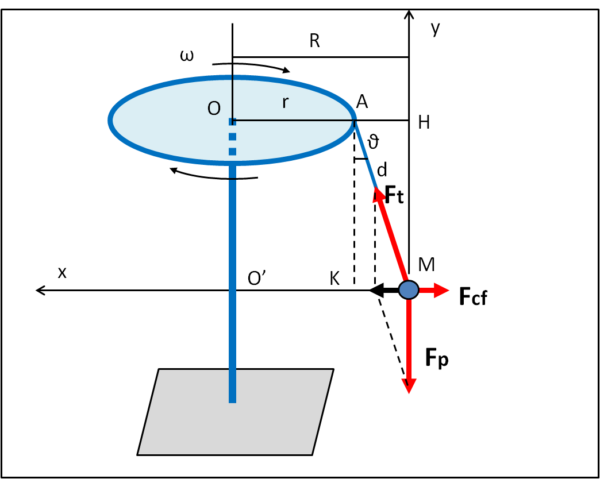
La coppia F_t e F_p darebbe come somma una forza diretta verso il palo, ma dovendo avere la somma totale uguale a zero, si deve introdurre una forza uguale e contraria, ossia F_cf, che altri non è che la forza centrifuga. Essa serve per annullare la somma delle forze in gioco. In pratica,  sembrerebbe solo "apparente", ma non lo è per la massa M che la sente... e come!

Possiamo scrivere:

F_p + F_t + F_cf = 0

Passando alle componenti in un sistema di riferimento solidale con la massa M, abbiamo :

F_cf = F_t sin θ

F_t cos θ= F_p

Ossia:

F_t = F_p/cos θ

sostituendo...

F_cf = F_p sin θ/cos θ

F_cf = M g tan θ

M a_cf = M g tanθ

a_cf = g tanθ

che è esattamente uguale alla (3) della trattazione precedente. Inserendo velocità angolare e periodo, si ottiene, ovviamente, lo stesso risultato precedente...

N.B.: Non è mai inutile ribadire la differenza tra forza centripeta e forza centrifuga. Immaginiamo, per semplicità, di avere una massa M che ruoti attorno a un punto O a cui è legata attraverso una corda. Per un osservatore esterno, la massa subisce solo la forza di tensione della corda che la costringe a muoversi di moto circolare uniforme. Per la massa M tutto appare fermo, però la corda è inspiegabilmente tesa. L'unico modo per spiegarlo è che esista una forza uguale e contraria alla forza di tensione che l'annulli e regali una situazione di immobilità.