(QI) Evviva la bandiera britannica * (***)
Un quiz geometrico con risposta veramente immediata, soprattutto se si conosce la ... bandiera britannica!
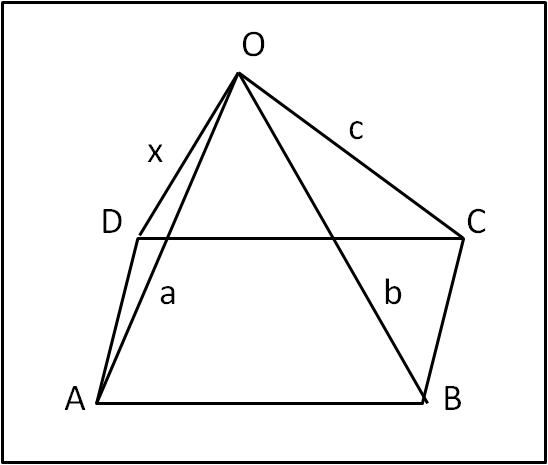
Consideriamo la strana piramide a base rettangolare della figura che segue. Essa ha i quattro spigoli laterali tutti diversi tra loro. Ne conosciamo solo tre (a, b e c). Domanda a bruciapelo: Quanto vale il quarto (x) in funzione degli altri tre?
Basta un solo passaggio...






16 commenti
Come primo impatto direi:
puoi anche scrivere il perché, tanto sarai l'unico...
Mi pare che Andy abbia ragione, perché senz'altro le diagonali del rettangolo di base sono uguali. Ma non vedo la relazione with the British flag
Un collegamento con la bandiera c'è. In particolare se si analizza come si è evoluta.
Il rettangolo con le diagonali è tipico della componente scozzese (croce di sant'Andrea) e irlandese (croce di San Patrizio)
E del Galles, che, a mio modesto parere, ha la bandiera più bella, non v’è traccia…
Caro Albertone,
le diagonali sono uguali, ma qui non stiamo utilizzando le diagonali... la perpendicolare tracciata da O al piano della base NON cade nel centro del rettangolo, ma in un punto V qualsiasi. La piramide vista dall'alto diventa come segue...
Caro Mau,
in realtà il collegamento alla bandiera sembra poco centrato, ma il nome non l'ho inventato io...
Se gli angoli AVC e BVD fossero ambedue retti allora le due diagonali (uguali tra loro) sarebbero le ipotenuse di due triangoli rettangoli (AVC e BVD) e quindi si arriverebbe alla formulazione di Andy (grande).
I piani su cui giacciono i due triangoli vanno ad intersecare il rettangolo di base esattamente lungo le diagonali.
Ho cercato di risolvere partendo dalla visione tridimensionale della piramide in oggetto, che è una piramide obliqua a base rettangolare (obliqua perché il piede dell’altezza non ricade sul piano del rettangolo nel suo punto centrale, ovvero il punto dove si incontrano le diagonali oppure gli assi dei lati minore e maggiore).


Detti rispettivamente L ed l i lati maggiore e minore del rettangolo, ho cercato di analizzare il caso particolare in cui l’altezza h della piramide poggia il piede su uno dei vertici del rettangolo di base, per cui la stessa altezza coincide con uno spigolo;
si evidenziano allora i triangoli rettangoli alx (ipotenusa x), aLb, adc perpendicolari al piano della base rettangolare e applicando il teorema di Pitagora:
In un secondo caso particolare, il piede dell’altezza h ricade sul lato minore l del rettangolo suddividendolo secondo un rapporto 2:1 (2/3 e 1/3, ma il rapporto proporzionale può essere un numero qualunque) evidenziando i triangoli rettangoli h_(2/3)l_a , heb, hfc, h_(1/3)l_x, sempre perpendicolari al piano della base rettangolare, e applicando il teorema di Pitagora:
La sostanza del ragionamento non cambierebbe se il piede dell’altezza h ricadesse su un punto qualsiasi del lato maggiore L.
Se il punto podale ricade ovunque tranne che al centro del rettangolo, basta calcolare le distanze del punto stesso da un lato minore e da un lato maggiore per evidenziare triangoli rettangoli come sopra.
Nel caso del punto podale coincidente con il centro del rettangolo, la relazione tra gli spigoli è altrettanto valida e, ovviamente, immediata.
Concludendo, in una piramide a base rettangolare o quadrata, regolare oppure obliqua, le somme dei quadrati degli spigoli contrapposti si equivalgono.
cari amici,
esiste un teorema chiamato proprio della "British Flag". Esso dice:
Se P è un punto interno al rettangolo ABCD, allora la somma dei quadrati delle distanze da P da due vertici opposti è uguale alla somma dei quadrati delle distanze rispetto agli altri due vertici opposti.
AP2 + PC2 = BP2 + PD2
I triangoli che queste distanze formano con il vertice della piramide sono tutti rettangoli con la stessa altezza, per cui si possono inserire gli spigoli laterali al posto delle distanze da P ai vertici.
La dimostrazione del teorema non ha bisogno di fare casi particolari e la riporterò nella soluzione...
Per il teorema di Varignon , un rettangolo è il parallelogramma di un quadrilatero
avente lati i cui punti mediani coincidono con i vertici del rettangolo.
Inoltre, poiché si tratta di un rettangolo, le diagonali del quadrilatero sono ortogonali.
Il quadrilatero e il rettangolo inscritto possono intendersi come lo sviluppo piano della piramide.
Un altro teorema ci dice che in un quadrilatero a diagionali ortogonali la somma dei quadrati dei lati opposti si eguagliano.
da cui l'asserto.
a^2 +b^2 = c^2 + x^2
La dimostrazione del teorema "della bandiera inglese" è abbastanza semplice:
La costruzione sul piano bidimensionale può essere vista come la proiezione della piramide esistente nello spazio tridimensionale; allora i segmenti c, d, e, f rappresentano, rispettivamente, le proiezioni degli spigoli
C, D, E, F della piramide, mentre il punto P è la proiezione del vertice della piramide stessa sul piano della base.
E siccome la distanza tra vertice della piramide e il punto P è l’altezza della piramide stessa, si possono visualizzare quattro triangoli rettangoli che condividono un'altezza comune h:
chC, dhD, ehE, fhF
dove la prima lettera minuscola rappresenta il cateto di base, la seconda minuscola l'altezza comune e la terza maiuscola l'ipotenusa-spigolo; per cu applicando il teorema di Pitagora:
Verrebbe da pensare che il rettangolo-bandiera inglese, o l'interessante quadrilatero citato da Leandro ( in cui le diagonali sono perpendicolari), siano gli unici casi in cui la somma dei quadrati delle distanze dal vertice V per una coppia di punti opposti è identica a quella per l'altra coppia di punti.
Viceversa questi casi rientrano in una famiglia di infinite configurazioni con la stessa caratteristica.
Consideriamo inizialmente due rette r1 ed r2 tra loro perpendicolari.
Il loro punto di intersezione è individuato dalla lettera A.
Scegliamo sulla retta r1 un punto B a distanza qualsiasi da A e sulla retta r2 un punto C a distanza qualsiasi da A.
Da un qualsiasi punto V appartenente allo spazio tridimensionale tracciamo i segmenti VA VB VC
Ora consideriamo i loro quadrati VA^2 , VB^2 , VC^2
La somma algebrica VB^2 + VC^2 – VA^2 = R^2 è il quadrato del raggio di una sfera che ha centro nel punto V.
Pertanto tutti i punti della superficie di questa sfera godono della medesima proprietà citata all'inizio.
In particolare considerando il cerchio che si ottiene intersecando la sfera con il piano individuato dai punti ABC, tra gli infiniti punti di questa circonferenza troviamo il punto D collocato all'intersezione della parallela a r1 passante per A con la parallela a r2 passante per B .
Questo ABCD non è altro che il rettangolo assegnato nel quiz sulla “bandiera inglese”.
Tra le altre infinite configurazioni ottenibili scegliendo un punto della circonferenza, troviamo anche quadrilateri a diagonali perpendicolari ( caso di Leandro) ma anche configurazioni in cui le diagonali non sono perpendicolari.
Ma c'è di più, se consideriamo come punto D un punto della sfera che non appartenga anche al piano ABC, otteniamo infiniti tetraedri invece di semplici quadrilateri.
Ad esempio, fisso questi valori di coordinate:
punto A(0,0,0) origine degli assi punto B(2,0,0), punto C(0,1,0), vertice V (1,1,1)
Calcolo il raggio della sfera R = radq ( VB^2 + VC^2 – VA^2) = radq(3+2-3) = radq(2)
Se rimango sul piano, scegliendo il punto D (2,1,0) ottengo un rettangolo come quello del quiz.
Sempre sul piano ma con D(1,2,0) ottengo un quadrilatero con diagonali perpendicolari;
ancora sul piano posso avere valori di coordinate D che individuano quadrilateri con diagonali NON perpendicolari, oltre a una configurazione in cui il punto D cade addirittura sul segmento AB, dando origine ad un quadrilatero degenere in cui tre punti (ADB) risultano allineati.
Nello spazio posso avere D (0,0,1) che forma con ABC un bel tetraedro “inchiodato” agli assi cartesiani, oppure D(1,1, 1+radq(2) ) che forma con ABC un altro tetraedro, oppure svariate altre soluzioni che formano altrettanti tetraedri talvolta con particolari configurazioni e simmetrie.
Insomma, ce n'è per tutti i gusti...
Sì Maurizio, mi hai capito. Sapevo che non si trattava di una piramide retta (non si chiamano così?) e quindi che i triangoli AVC e BVD non erano perpendicolari alla base, ma inclinati. Non ho tenuto conto però che solo se i loro angoli al vertice V fossero stati retti avrei potuto scrivere a^2+c^2 = b^2 + x^2 come ha scritto Andy.
Ottimo Andy...
Albertone, non capisco tutte queste ipotesi, quando tutto è estremamente semplice. Vedi soluzione... L'importante è che siano rettangoli i triangoli OPA e simili. P è il piede della perpendicolare da O al piano del rettangolo.