Categorie: Matematica
Tags: area geometria quiz triangolo rettangolo un solo cateto noto
Scritto da: Vincenzo Zappalà
Commenti:1
Dato un solo lato è possibile determinare l'area di un triangolo? ** (con soluzione)
Conosciamo molto bene come si calcola l'area di un triangolo: base per altezza diviso per due. E se il triangolo fosse rettangolo? Beh... le cose non cambierebbero, al limite potremmo dire che basta moltiplicare i due cateti tra loro e dividere il risultato per due.
Da quanto detto si evince che se l'unico termine noto del problema fosse un cateto, alla mia richiesta di calcolare l'area mi rispondereste: "Ci manca qualcosa... esistono infiniti triangoli rettangoli che hanno lo stesso cateto. E, quindi, esistono infiniti valori dell'area del triangolo".
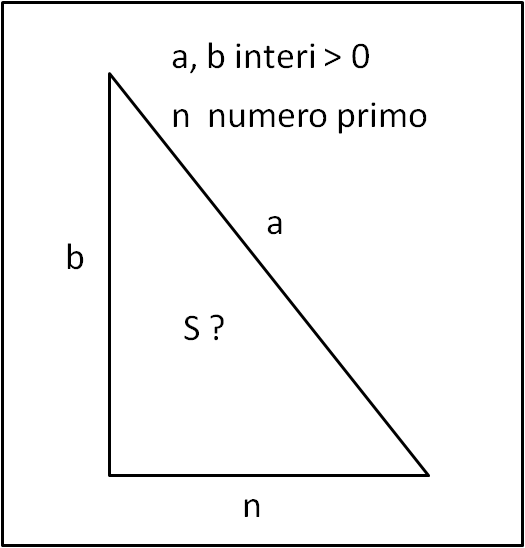
E se vi dicessi che il cateto conosciuto è un numero primo e che gli altri due lati devono essere interi positivi maggiori di zero ? Cambierebbe qualcosa?
Il nostro quiz si può, quindi, riassumere come segue:
Quante sono e come si possono esprimere le aree possibili di un triangolo, in funzione del cateto conosciuto?
SOLUZIONE
La risposta al quiz è SICURAMENTE SI, dato che per n primo, diverso da 2, esiste un solo triangolo rettangolo che ammette n come cateto.
Il nostro Andy ha risolto il problema utilizzando immediatamente una proprietà delle terne pitagoriche. Noi, però, vogliamo far finta di non conoscere questi speciali triangoli rettangoli e ricavare, comunque, la formula finale, attraverso tutti i passaggi logici.
Iniziamo col dire che
a > 0 intero
b > 0 intero
Il triangolo è rettangolo e l’ipotenusa è a. Per cui
a > b
essendo a e b interi, anche
a + b intero
a – b intero
Il teorema di Pitagora ci dice che:
a2 = b2 + n2
ossia:
a2 – b2 = n2
(a + b)(a – b) = n2 .... (1)
Il che vuol dire che sia (a – b) che (a + b) sono DIVISORI di n2. Ma n è un numero primo, per cui il suo quadrato può essere divisibile solo per n e per 1. L’uguaglianza precedente può essere soddisfatta solo in tre modi:
1 ∙ n2 = n2 …. (2)
n ∙ n = n2 …. (3)
n2 ∙ 1 = n2 …. (4)
Tuttavia la (3) è da scartare dato che non può essere a = b = n, poiché a è l’ipotenusa e deve essere maggiore di b. E’ da scartare anche la (2), dato che dovrebbe essere b = n2 > a.
Rimane possibile solo la (4)
n2· 1 = ( a + b) ( a – b) = n2
Possiamo scrivere:
a + b = n2
a – b = 1
Cambiamo il segno alla seconda
a + b = n2
- a + b = - 1
Sommiamo le due relazioni:
2b = n2 – 1 …. (5)
b = (n2 – 1)/2
L’area è quindi data da:
S = ½ b n
S = ¼ n (n2 – 1)
Ne segue che dato n, numero primo, l’area è univocamente determinata.
c. v. d.
Il caso con n = 2 è da scartare, ricordando la (5), in quanto è l’unico caso che con n primo si ottiene 2b = n2 – 1 dispari e, quindi, b deve essere frazionario.
Per n primo ≠ 2, n2 è sempre un numero dispari, per cui 2b = n2 – 1 è sempre pari e, quindi, divisibile per 2, ossia b è intero.
Ovviamente a è sempre intero dato che è uguale a b + 1, entrambi numeri interi.
Per n = 3, otteniamo la classica terna pitagorica (3, 4, 5), la cui area vale 6.
b = (9 – 1)/2 = 4
a = b + 1 = 5






1 commento
Mi ricorda qualcosa...
Per come è presentata la figura, evinco che il cateto minore ha come misura un numero primo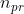 , b è il cateto maggiore e a l'ipotenusa.
, b è il cateto maggiore e a l'ipotenusa.
Allora nell’insieme delle terne pitagoriche potrei considerare il sottoinsieme composto da quelle terne dove il cateto minore è un numero primo e l'ipotenusa supera di una unità il cateto maggiore, ovvero a = b + 1:
ad esempio le terne 3, 4, 5 ; 5, 12, 13 ; etc.
Diventa allora immediato scrivere: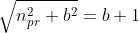 che sviluppata e risolta per b da come risultato:
che sviluppata e risolta per b da come risultato:
n = 3 , b = 4
n = 7 , b = 24
E dato che l'area del triangolo rettangolo è pari al semi-prodotto dei cateti, si può scrivere:
n = 5 ; Area = 30
n = 11 ; Area = 330