Categorie: Fisica di Papalla
Tags: moto aereo Papalla quiz uovo dinamico
Scritto da: Vincenzo Zappalà
Commenti:4
A proposito di uova ... (con soluzione) **
Sul pianeta Papalla, la Pasqua si festeggia con un gioco molto divertente e un po' spericolato. I papallicoli devono descrivere un uovo "dinamico", ossia la traiettoria che devono seguire ha una forma che ricorda molto quella di un uovo. Nessun pericolo, comunque: i papallicoli possono tranquillamente rimbalzare al suolo senza subire danni, la gravità è del tutto simile a quella della Terra, non esiste atmosfera e, infine, essi sanno costruire superfici perfettamente lisce.
Un papallicolo di massa m è posto nel punto più basso di una struttura circolare che si interrompe ad un’altezza pari a 4/3 del suo raggio. Che velocità bisogna impartire al papallicolo affinché, scivolando lungo la parte interna della struttura circolare, riesca a tornare al punto di partenza lungo la stessa struttura?
L'uovo che devono percorrere è raffigurato nella figura che segue.
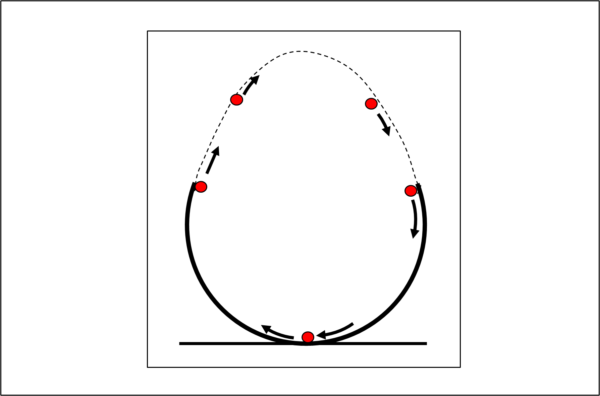
SOLUZIONE
Tralasciamo, per il momento, il moto del papallicolo da O al punto finale del tratto circolare P. Esso arriva in P con una certa velocità v1, legata ovviamente alla velocità vo che gli è stata impartita in O.
In poche parole, giunto in P il papallicolo viene lanciato nello spazio con una certa velocità, tangente al cerchio, che forma un angolo θ con la direzione orizzontale. L'angolo θ è lo stesso che individua la posizione di P rispetto al centro cerchio. Solitamente, l'altezza di P rispetto ad O vale 3/4 del raggio del cerchio.
Siamo di fronte a un classico moto parabolico, che dovremmo conoscere molto bene. Un moto, però, che ha dei vincoli ben precisi: deve far tornare il papallicolo sulla direzione orizzontale esattamente nel punto Q, in modo da continuare a scivolare fino a O.
Iniziamo col calcolare la distanza PQ = sx, ossia il tragitto orizzontale che deve essere compiuto dal papallicolo. Poniamo l'origine delle coordinate x e y nel punto P con il verso positivo illustrato nella Fig. 1.
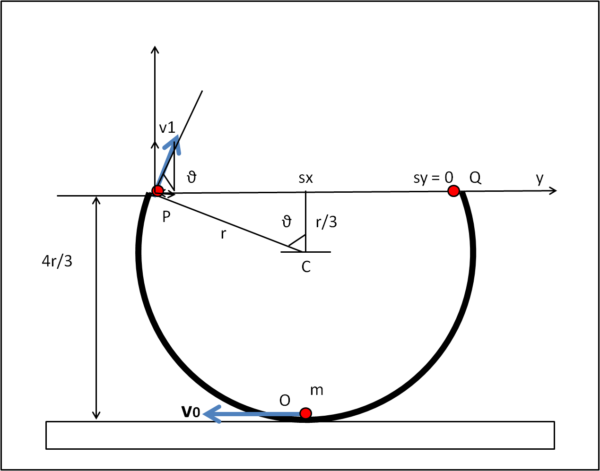
Conoscendo il raggio r del cerchio, è immediato scrivere:
PQ = sx = 4√(r2 - r2/9) = 4r√2/3 .... (1)
Il papallicolo viene proiettato fino a una certa altezza h (ne parleremo dopo), ma. giunto in Q, deve tornare ad avere la stessa ordinata, ossia sy = 0.
Possiamo calcolare il valore del seno e del coseno dell'angolo θ che ci serviranno per separare le coordinate della velocità v1.
sx/2 = 2r√2/3 = r sin θ
sin θ = 2√2/3 .... (2)
r/3 = r cos θ
cos θ = 1/3 .... (3)
Fatti questi semplici calcoli matematici, possiamo occuparci dl moto parabolico del papallicolo. La sua velocità v1 in P può essere scomposta nelle due componenti v1x e v1y, che possono essere scritte come:
v1x = v1 cos θ
v1y = v1 sin θ
sul papallicolo agisce inoltre l'accelerazione di gravità diretta verso il basso, ossia:
ay = - g
Lungo l'asse delle x il moto è rettilineo uniforme, lungo l'asse delle y il moto è uniformemente accelerato. Conosciamo bene le formule che descrivono questo tipo di moti, ed esse ci dicono, avendo posto l'origine del moto in P, che, nel primo caso:
sx = vx t
e, nel secondo caso
sy = vy t + 1/2at2
Cominciamo a scrivere la seconda che ci fornisce il tempo di volo. Infatti, dato che sy = 0, abbiamo:
0 = v1 t sin θ - 1/2 g t2
t = 0 è opzione da scartare e, quindi:
t = 2 v1 sin θ/g .... (4)
Conoscendo sin θ dalla (2), possiamo scrivere:
t = 4 v1 √2/(3g) .... (5)
La prima ci dice, invece, che:
sx = v1 t cos θ
sostituendo t, abbiamo:
sx = v1 cos θ (4 v1 √2/(3g))
Ma conosciamo cos θ dalla (3) e, sostituendo, otteniamo:
sx = (v1 1/3) (4 v1 √2/3g)
Conosciamo sx dalla (1) , per cui:
4r√2/3 = (v1 1/3) (4 v1 √2/3g)
semplificando:
r = v12/3g
v12 = 3gr .... (6)
Abbiamo determinato la velocità necessaria per compiere il balzo nel vuoto e ricadere in Q e, di conseguenza, in O.
In realtà, però, il problema ci chiede la velocità v0 che bisogna impartire al papallicolo che, non sarà, ovviamente, uguale a v1. A questo punto basta ricordarsi la conservazione dell'energia. Quando il papallicolo è in P e viene lanciato, la sua energia potenziale può essere posta uguale a zero, mentre la sua energia cinetica vale 1/2 m v02. In poche parole, la sua energia totale è:
E0 = 1/2 mvo2 + 0 = 1/2 mvo2
Quando il papallicolo giunge in P, ha sicuramente perso parte dell'energia cinetica (la sua velocità v1 è sicuramente minore di vo), ma ha guadagnato dell'energia potenziale che, come sappiamo, è data da mgh, dove h, nel nostro caso, vale 4r/3. Come detto, l'energia si deve conservare, per cui:
E0 =EP
1/2 m vo2 = 1/2 mv12 + m g 4r/3
Conosciamo v12 dalla (6) e, quindi:
1/2 m vo2 = 3 m gr/2 + 4 mgr/3
3/6 v02 = 9 /6 gr + 8/6 gr
v02 = (17gr/6)(6/3)
v02 = 17 gr/3
v0 = √(17 gr/3)
Senza bisogno di ricavarla nuovamente, possiamo ricordare la formula che ci regala l'altezza massima raggiunta dal papallicolo durante il suo volo:
ymax = v12 sin2 θ/(2g) = 3gr · 8/(18 g) = 3 gr · 2 · 4/(6 · 3 g)
ymax = 4r/3
L'altezza raggiunta in volo è esattamente h, quella che separa il punto di partenza dal bordo della rampa di lancio, ossia OP. Un uovo niente male (Fig. 2)!

Viva i papallicoli!!





4 commenti
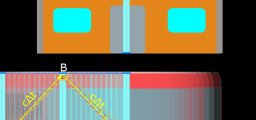
Magari sbaglio, ma mi viene in mente il moto parabolico di un proiettile, con gittata pari ad AB e velocità v misurata nel punto A:
ops... ho appena pubblicato la soluzione passo per passo, ricordando il moto parabolico e non solo.
Caro Enzo,
la tua soluzione/spiegazione del problema, oltre che ineccepibile, è perfetta da un punto di vista fisico/matematico e didattico.
La mia ha qualcosa di "ingegneristico/balistico", limitandosi alla misurazione della velocità "di sparo" (che coincide con quella da te ricavata ma per raggio = 1) a partire dal punto in cui finisce l'arco di cerchio e inizia quello di parabola, semplificando al caso di arco di cerchio di raggio unitario.
Può essere interessante notare che velocità, altezza raggiunta e gittata sono indipendenti dalla massa dell'oggetto, visto che il rapporto con la massa del pianeta è pressoché nullo (ma l'interazione gravitazionale di m verso M esiste anche se infinitesima ).
).
grazie Andy per le precisazioni!
Il nostro colloquio personale continua attraverso i quiz...