Categorie: Matematica
Tags: equilibrio geometria quadrato incernierato quiz
Scritto da: Vincenzo Zappalà
Commenti:8
(Q) Come bloccare una caduta (con soluzione)**
Questo quiz è di pura geometria, ma ho voluto presentarlo come se fosse relativo a un problema di equilibrio, per dimostrare quanto sia importante la geometria nella risoluzione di problemi di meccanica classica.
Al bordo di un tavolo viene posto il quadrato verde (ABCD). Al suo fianco, sospeso nel vuoto si inserisce un altro quadrato azzurro (DEFG), incernierato al primo in D. Ovviamente, questo secondo quadrato comincia a cadere ruotando attorno a D, ma viene subito bloccato con una corda BG (blu) di lunghezza unitaria. La situazione è un po' precaria e si decide di aggiungere un ulteriore corda rossa (AF) che tenga il quadrato azzurro in perfetto equilibrio. Le due corde risultano entrambe ben tese.
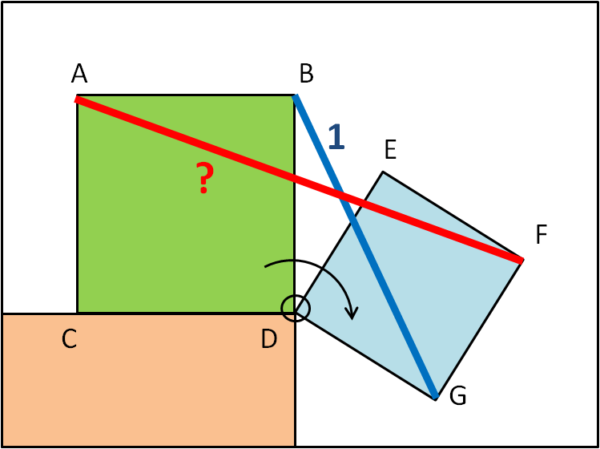
Si chiede:
Quanto deve essere lunga la corda rossa AF ?
N.B.: Il tutto deve essere svolto nel minor tempo possibile e non vi è, quindi, tempo di effettuare calcoli. In poche parole, la lunghezza di AF deve essere determinata " a mente", senza nessun passaggio matematico.
Forza Andy e Leandro, sperando che si aggiunga anche un terzo incomodo (o magari molti di più... la speranza è l'ultima a morire!)
SOLUZIONE
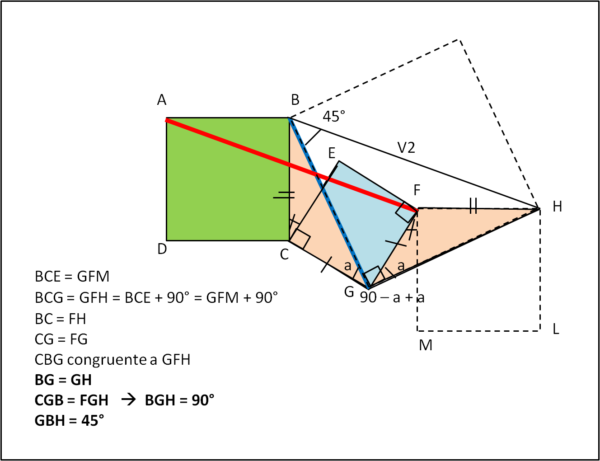
Dopo quanto riportato da Andy nei commenti parrebbe inutile aggiungere altro. Tuttavia, per dimostrare ancora una volta la varietà delle soluzioni geometriche possibili, aggiungo un metodo altrettanto semplice e non bisognoso di calcoli. Per mostrarlo basta la figura che segue...
8 commenti
AF= 1 x radice di 2
caro Silvano,
aggiungi anche il metodo usato per ottenere il risultato...
perfetto Andy. Nella soluzione inserirò un modo altrettanto semplice, ma sicuramente più lungo
Per curiosità ho provato con due quadrati i cui lati stanno secondo un rapporto qualsiasi (nell'esempio che riporterò è 5:2) e con il quadrato "in bilico" inclinato di un angolo qualsiasi (nell'esempio 36°):
Parimenti ho "smontato" il segmento rosso, inclinato di 45° è adagiato sugli estremi liberi dei due L.
Sembrerebbe che, in una struttura così configurata, il rapporto (segmento rosso) / (segmento blu) sia costante e pari a
, indipendentemente dal rapporto tra i lati dei due quadrati e dall'angolo di inclinazione del quadrato più piccolo....
Confermo quanto sopra:
I due triangoli ADF e BDG sono simili. L'angolo in D uguale 90°+∠BDE e i lati che lo compendono in proporzione (diagonali dei quadrati per ADF e lati del quadrato per Bla daigonale e il alto di un quadrato.DG.
Pertanto anche AF e BG sono in rapporto come
Nella fretta di scrivere non mi sono accorto che il cursore è saltato.
Ricompongo.
I due triangoli ADF e BDG sono simili. L'angolo in D uguale 90°+∠BDE e i lati che lo compendono in proporzione (diagonali dei quadrati per ADF e lati dei quadrati per BDG).
Pertanto anche AF e BG sono in rapporto come la daigonale e il lato di un quadrato.