Affrontiamo passo dopo passo la possibilità di cambiare il dominio  di un integrale doppio per rendere il tutto più rapido e "facile".

Area di un parallelogramma e determinante

Non ci sarebbe bisogno di scrivere questo primo articolo, dato che l'argomento è stato abbondantemente discusso QUI (da area di un parallelogramma fino all'appendice inclusa.....). Tuttavia, è meglio riportare i risultati ed eseguire una semplice dimostrazione che fornirà chiaramente il significato geometrico del determinante di una matrice quadrata.

Ricordiamo che se abbiamo una matrice M

 

 

 

il suo determinante D

 

 

 

ha il valore:

D = a1 b2 - b1 a2

Vogliamo dimostrare che il determinante di una matrice quadrata è l'area di un parallelogramma che ha come lati due vettori v1 e v2, le cui componenti sono x1, y1 e x2,y2.

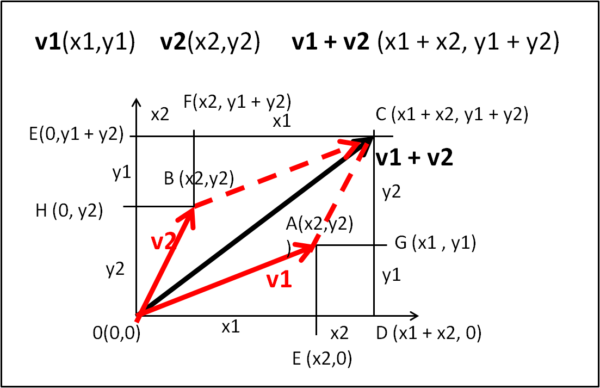
Consideriamo la Fig. 1 e due vettori qualsiasi v1 e v2 di coordinate x1, y1 e x2, y2, rispettivamente. Il vettore v1 + v2 ne è la loro somma (regola del parallelogramma).

Consideriamo ora la matrice quadrata M che ha come colonne le componenti dei due vettori:

il suo determinante D

è dato da:

D = x1 y2 -  x2 y1

N.B.: potremmo anche inserire le due componenti del primo vettore nella prima colonna e quelle del secondo nella seconda. Niente cambierebbe e il risultato sarebbe lo stesso: provare per credere.

L'area A_R del rettangolo ODCE vale, ovviamente:

A_R = (x1 + x2)(y1 + y2)

Per ottenere l'area A_P del parallelogramma OACB dobbiamo togliere all'area A_R del rettangolo alcune parti...

Per l'esattezza, due volte l'area del triangolo OAE, due volte l'area del triangolo AGC e due volte l'area del rettangolo AGDE. E' banale scrivere queste aree:

2 A_OAE = x1 y1

2 A_AGC  = x2 y2

2 A_AGDE = 2 x2 y1

Per cui:

A_{P =} A_R - 2A_OAE - 2 A_AGC - 2 A_AGDE

A_P = x1 y1 + x1 y2 + x2 y1 + x2 y2 - x1 y1 - x2 y2 - 2x2 y1

A_P = x1 y2 - x2 y1 = D

c.v.d.

Perché tutto ciò?  Cosa c'entra con gli integrali?

Bene, un determinante come quello appena introdotto prende il nome di Jacobiano ed è fondamentale saperlo calcolare  -e tenerne conto- quando si vuole effettuare un cambio di coordinate nel calcolo di un integrale doppio, dato che fornisce il modo di calcolare la nuova area infinitesima del dominio.

continua ...