Categorie: Matematica
Tags: area due quarti di cerchio geometria quiz
Scritto da: Vincenzo Zappalà
Commenti:9
(Q) Due quarti di cerchio (con soluzione)***
Consideriamo la figura che segue:
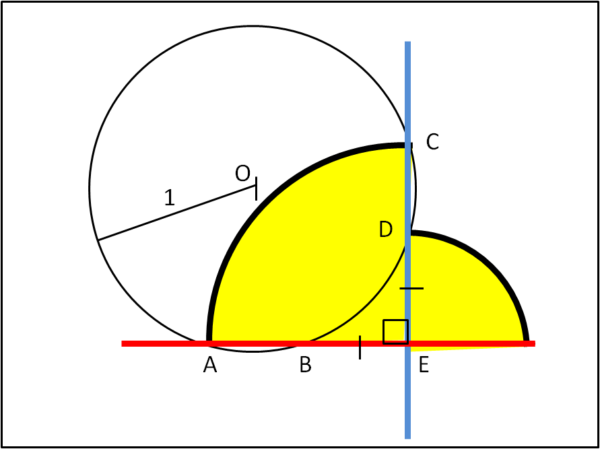
Tracciare la retta rossa che interseca la circonferenza di raggio unitario in due punti A e B. Dal punto E, tracciare la perpendicolare a questa retta tale che anch’essa intersechi la circonferenza in due punti C e D, imponendo che BE = ED.
Facendo centro in E disegnare due quarti di cerchio tali che il più grande abbia raggio AE e il più piccolo abbia raggio ED.
Si chiede:
Quanto misura l'area gialla ?
SOLUZIONE nei commenti... Andy è un perfetto collaboratore !!!
9 commenti
Ho la sensazione di "fiutare" π/2....
Per come è costruita la figura, le due corde AB e CD sono ottenute casualmente (in base alla distanza OE) ma comunque sempre della stessa lunghezza.
Allora nulla vieta di costruire la figura con le due corde AB e CD di misura pari al raggio unitario:
Per il teorema del coseno applicato al triangolo AOC posso scrivere:
ma il coseno di 150° è pari al coseno di 30° cambiato di segno ovvero=-&space;\frac{\sqrt&space;3}{2})
allora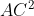
= 2 + √3 → AC = √(2 + √3)
Ma AC è anche l'ipotenusa del triangolo rettangolo isoscele AEC per cui EA = EC = √( (2 + √3)/2 )
e per differenza EB = ED = √( (2 + √3)/2 ) - 1
EB = ED e EA = EC sono i raggi delle due circonferenze concentriche, quindi la somma dei loro quadrati moltiplicata per π/4 da iol valore dell'area gialla; ma la somma dei due quadrati è pari a 2 per cui l'area gialla misura π/2.
Nel caso in cui le due corde AB e CD degenerano in due singoli punti:
Praticamente, fissato un determinato riferimento degli assi perpendicolari rosso e blu, per ogni traslazione contemporanea e dello stesso passo del rosso verso l'alto-basso e del blu verso sinistra-destra, le dimensioni delle due corde uguali AB e CD e di conseguenza dei due raggi EA ed EB, varieranno (quando un quarto aumenta l'altro rimpicciolisce e viceversa), ma la somma dei quadrati di tali raggi rimane costante e pari a 2,
Un caso generale in linea con l'ipotesi, utilizzando il teorema del coseno e le regole di trigonometria per gli angoli associati:
e senza trigonometria? Praticamente "a mente" ?
Caro Enzo
hai ragione, avevo la soluzione "in casa" e non me ne ero accorto....Vabbè, è valso come ripasso di trigonometria!
ottimo Andy... Io ho maneggiato un po' con trapezi isosceli, ma la relazione finale è la stessa...
Sia R il raggio EA ed r il raggio EB. Sia H la proiezione di O sulla corda, ad esempio, CD.
Si BH = (R+r)/2, mentre CH = (R-r)/2.
Per Pitagora, (R+r)^2/4 + (R-r)^2/4 = 1.
Cioè R^2+r^2 =2.
L'area cercata è R^2 π/4 + r^2 π/4, che, per la precedente, diventa π/2.
Se E è interno al cerchio, valgono le stesse formule con i ruoli scambiati.
AEC è rettangolo isoscele con ∠CAE = 45°. Questo implica che CB = √2. Ma CB ^2 = CE^2 + EB^2 = R^2 + r^2.
Il resto segue come sopra.