Categorie: Matematica
Tags: geometria Karel Petr poligono qulasiasi poligono regolare
Scritto da: Vincenzo Zappalà
Commenti:1
Il teorema di Petr: come trasformare un poligono qualsiasi in un poligono regolare ***
Un vero e proprio miracolo matematico e geometrico, a lungo sconosciuto e riscoperto in tempi più recenti. Oggi prende il nome di teorema di Petr - Douglas - Neumann, ma Il vero "padre" di questa inaspettata e splendida costruzione geometrica è, comunque, il matematico cecoslovacco Karel Petr che la pubblicò (in cecoslovacco...) nel 1905. In qualche modo essa è la generalizzazione veramente stupefacente del teorema detto di Napoleone, di cui avevamo già parlato raccontando la VERA storia del grande imperatore...
La dimostrazione del "miracolo" è oltremodo complicata e abbisogna dei numeri complessi. Noi ci limiteremo a raccontare i risultati di questo teorema. Chi vorrà divertirsi avrà modo di applicare la procedura a poligoni con un qualsiasi numero di lati e, magari, di fare qualche animazione
Iniziamo con un pentagono
La Fig. 1 riporta un pentagono qualsiasi ABCDE.
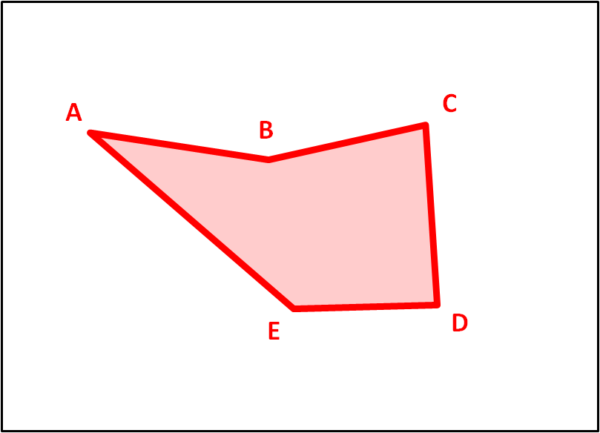
Sappiamo che gli angoli interni di un pentagono regolare valgono 72° (360/5) per cui costruiamo dei triangoli isosceli con l'angolo opposto alla base uguale a 72°. Questi triangoli (rossi) vanno posizionati sui lati del pentagono, verso l'esterno, come mostra la Fig. 2.
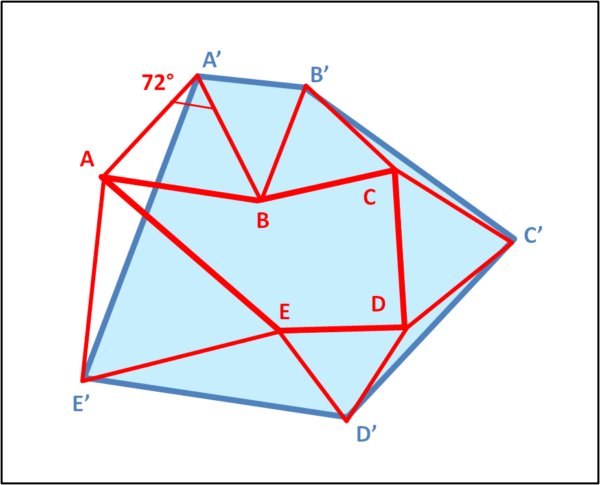
Uniamo i vertici A', B', C', D', E' di tali triangoli, ottenendo un nuovo pentagono (azzurro).
Lavoriamo su questo nuovo pentagono, inserendo nuovamente, in Fig. 3, dei triangoli isosceli (azzurri) sui suoi lati, come fatto precedentemente. Questa volta, però, l'angolo opposto alla base deve essere di 72 + 72 = 144°
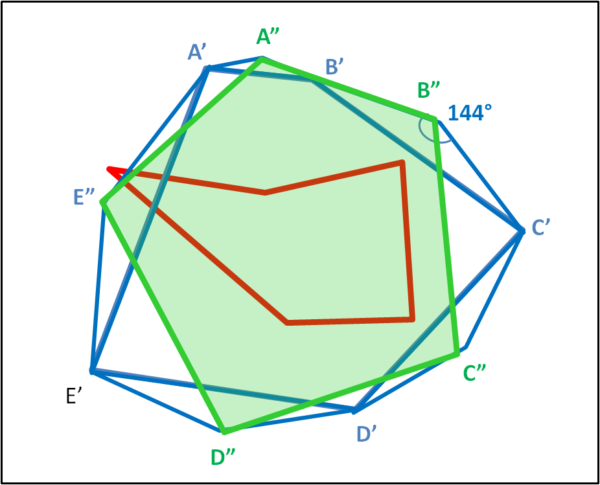
Abbiamo determinato dei nuovi vertici A", B", C", D", E" che uniamo tra loro in modo da costruire un nuovo pentagono (verde). Non vi sarà sicuramente sfuggito il fatto che quest'ultimo pentagono ha una forma ben più regolare di quello di partenza. Ci resta da fare, però, ancora un passo verso la ... perfezione. Aggiungiamo altri 72° all'angolo precedente, ossia consideriamo un nuovo angolo di 144 + 72 = 216°. Ovviamente, non esiste un triangolo isoscele con un angolo di 216°, tuttavia, se consideriamo il segmento A" B" possiamo costruire un triangolo (diretto verso l'interno del poligono), tale che l'angolo tra A", il nuovo vertice A"' e B" sia di 216°. Otteniamo, così, un nuovo pentagono (grigio) che ha per vertici A"', B"', C"', D"', E"' (Fig. 4).
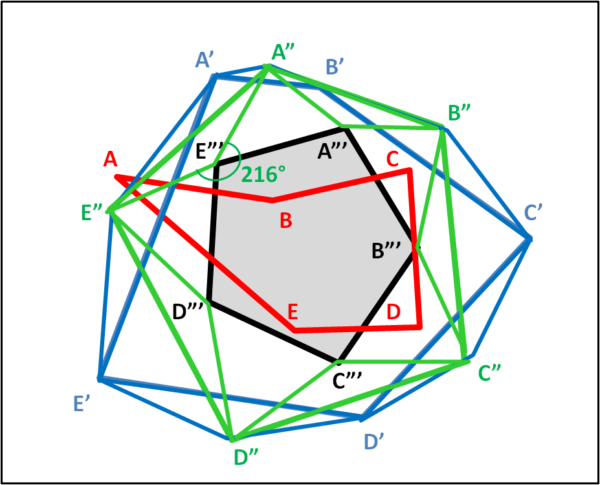
Bene... il pentagono grigio è un pentagono regolare, con tutti gli angoli (72°) e i lati uguali!
Vediamo di generalizzare il risultato e descrivere ancora meglio le procedure da eseguire...
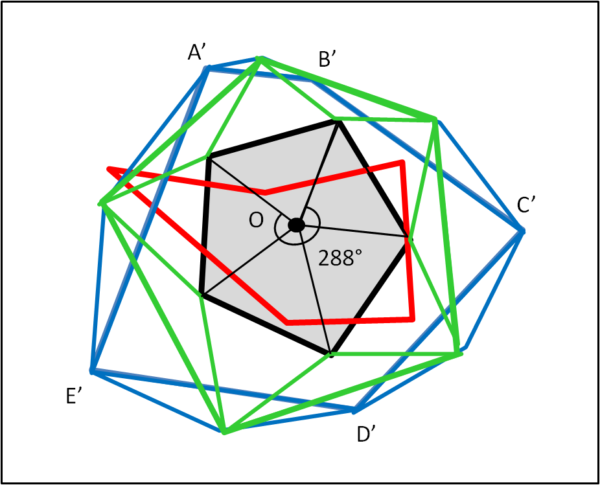
Innanzitutto, gli angoli da sommare sono sempre in numero uguale a n-2, dove n è il numero dei lati del poligono. Nel caso del pentagono n = 5 e quindi abbiamo sommato solo 3 volte l'angolo di partenza, che è sempre l'angolo interno relativo al poligono regolare. E' facile capire perché bastano n - 2 angoli. Lo dimostra la Fig. 5, dove abbiamo continuato la procedura sul poligono grigio, utilizzando un angolo di 216 + 72 = 288°. Ciò che si ottiene è, ovviamente, un solo punto O.
Illustriamo in dettaglio la procedura necessaria per costruire i triangoli isosceli o, se preferiamo, i nuovi vertici dei poligoni successivi. Per far ciò consideriamo la Fig. 6, dove è rappresentato un certo numero di lati di un poligono qualsiasi.
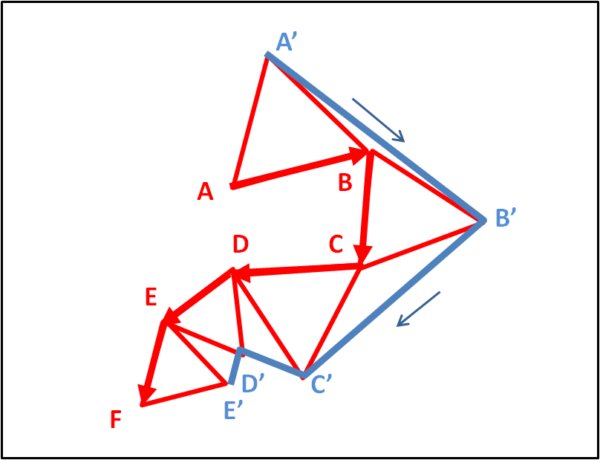
Iniziando da A, scegliamo un certo verso, indicato dalla freccia rossa. Il triangolo da costruire rimane sempre alla sinistra del verso quando l'angolo è minore di 180°, mentre si costruisce sulla destra quando supera 180°. Esattamente come abbiamo fatto durante la costruzione del pentagono. Attenzione! Possiamo anche partire da F e andare verso A, invertendo il verso di percorrenza, In questo caso i triangoli saranno diversi dal caso precedente, dato che devono essere sempre costruiti a sinistra rispetto al verso di percorrenza (e a destra per angoli maggiori di 180°). Alla fine otterremo ugualmente un pentagono regolare, diverso dal primo come dimensioni e orientamento, ma con lo stesso centro O. Una volta che è stato scelto il verso di percorrenza, esso deve essere sempre lo stesso per tutti i poligoni costruiti successivamente (come mostrano le frecce azzurre).
Primo esercizio: Potete divertirvi a costruire il pentagono precedente, muovendovi da A verso E, D, C, B.
Un'altra peculiarità della costruzione sta nel fatto che possiamo costruire i triangoli cambiando l'ordine degli angoli, ossia, ad esempio, prima utilizzare 216°, poi 72° e infine 144°: il risultato sarà lo stesso.
Come già ribadito, il numero di lati può essere qualsiasi e così anche la forma del poligono. Vediamo in Fig. 7 un decagono decisamente strano, dalla forma ad "otto" (linea rossa con vertici indicati da pallini rossi). Nessun problema! Seguendo le regole della costruzione appena descritte arriveremo a un decagono regolare.
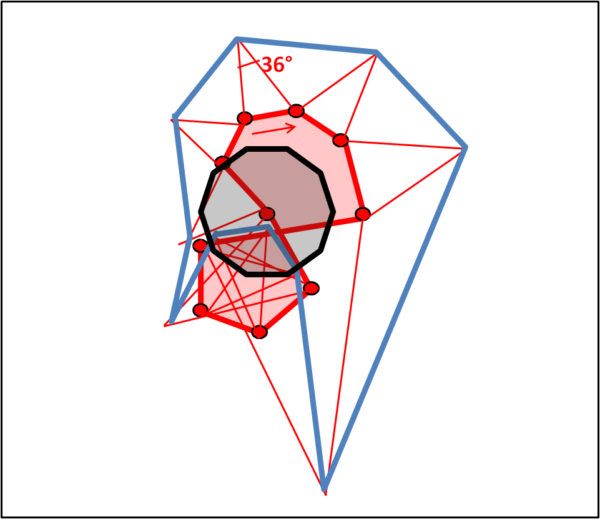
All'inizio tutto è facile, ma quando si arriva nella parte bassa è fondamentale ricordare la regola della sinistra. I triangoli sembrano diretti verso l'interno del decagono di partenza, ma la regola è rispettata.
Secondo esercizio: Potete completare il decagono regolare continuando dopo il decagono azzurro. Alla fine dovrete trovare il decagono grigio che è regolare! Ovviamente, cambiano gli angoli... Il primo sarà dato da 360/10 = 36°, poi 36 + 36 = 72°, poi 72 + 36 =108° e via dicendo fino a 36 x 8 = 288°.
Una costruzione non semplice, sicuramente, che può creare confusione... Magari potete ideare un qualche programmino che esegua i vari passaggi...
Abbiamo lasciato per ultimo il caso più semplice, quello relativo al triangolo. Esso permette di costruire un triangolo equilatero, partendo da un qualsiasi triangolo, come mostra la Fig. 8.
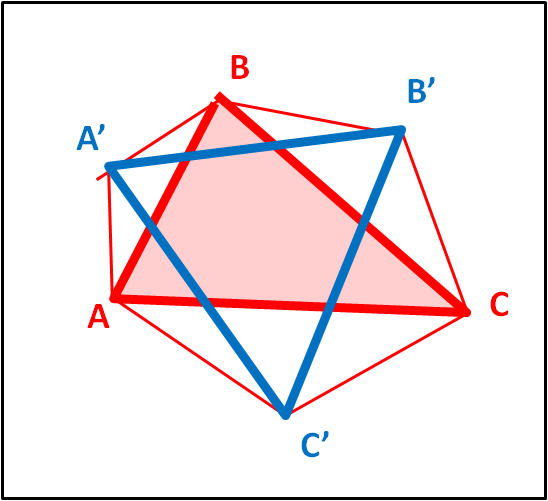
Questo caso è quello che ci riporta al teorema di Napoleone. Ovviamente, in questo caso basta un solo passaggio (3 - 2 = 1) e un angolo di 360/3 = 120°
Le peculiarità del teorema di Petr non finiscono qui. A seconda di come verrà accolto questo articolo potremmo anche entrare nei dettagli...






1 commento
Caro Enzo,
come sempre la Geometria è fonte inesauribile di meraviglie.
No so (ma lo so ) se hai di proposito saltato il caso dei quadrilateri, ma mi permetto di tirarlo fuori io:
) se hai di proposito saltato il caso dei quadrilateri, ma mi permetto di tirarlo fuori io:
seguendo il metodo e le regole di costruzione, la prima batteria di 4 triangoli isosceli è composta da triangoli rettangoli isosceli (360/4=90) che danno luogo al primo quadrilatero di trasformazione;
ma la seconda batteria di triangoli isosceli è composta da triangoli degeneri (l'angolo al vertice diventa piatto: 90+90=180) per cui è sufficiente unire i punti medi del primo quadrilatero di trasformazione per ottenere un quadrato:
Nella figura ho "quadruplicato" i singoli triangoli rettangoli isosceli per visualizzare in tratteggio i corrispondenti quadrati, utilizzando cosi' la stessa costruzione usata per la dimostrazione del teorema di Van Aubel (qui il link con la tua dimostrazione di questo interessante teorema: http://www.infinitoteatrodelcosmo.it/2021/12/26/qi-un-nuovo-teorema-dalla-conclusione-inaspettata-2-la-dimostrazione-vettoriale/ ) che quindi rappresenta un caso particolare del teorema di Petr.
Può essere più o meno interessante il fatto che, se il quadrilatero "padre" è ciclico, il quadrilatero "figlio" eredita dal "padre" la caratteristica dell’essere ciclico (non l'ho dimostrato ma penso che "giocando" un po con gli angoli si arrivi alla dimostrazione):