Pitagora, Euclide e molti altri antichi e geniali greci hanno praticamente scoperto e descritto tutto ciò che c'è da sapere sulla geometria. In particolare, i triangoli e le loro proprietà sono stati analizzati in tutti i loro dettagli. Ma è proprio vero? Sembra proprio di no...

Lee Cecil Fletcher Sallows... chi lo conosce? penso  ben poche persone, anche tra gli amanti della geometria classica. Eppure, circa dieci anni fa egli ha scoperto una nuova proprietà dei triangoli qualsiasi che lascia "di stucco". Come non averlo notato prima?!

In particolare, ci riferiamo alle mediane di un triangolo qualsiasi. Ricordiamo tre delle fondamentali caratteristiche di queste linee speciali. Come sappiamo, esse uniscono i vertici con il punto di mezzo dei lati opposti. Ne segue che il loro punto di incontro (baricentro) divide le mediane in due parti, l'una doppia dell'altra. Inoltre, le mediane dividono il triangolo in due triangoli di uguale area e, come facile conseguenza,  esse individuano sei  triangoli all'interno del triangolo di partenza che hanno tutti la stessa area, ossia sono equivalenti. La Fig. 1 riposta quanto detto:

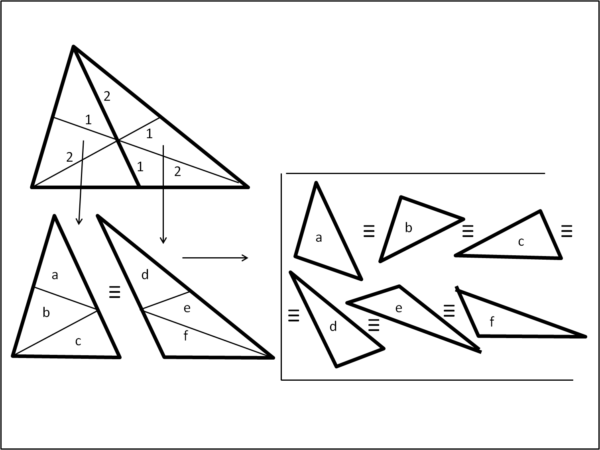
Il nostro matematico Sallows, creatore anche di molti giochi matematici, ha, però, eseguito un'operazione non certo complicata. La vediamo in Fig. 2, dove i sei triangoli equivalenti sono stati colorati per una migliore visualizzazione.

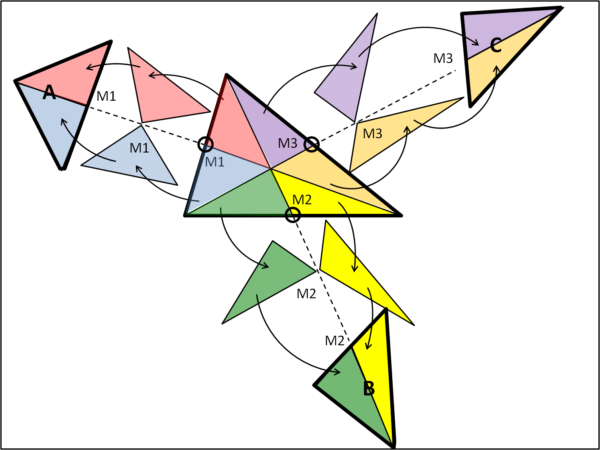
Scegliamo M1, M2 e M3 (punti di mezzo dei lati) come centri di rotazione e ruotiamo i triangoli colorati a due a due attorno a questi punti, come mostrato nella figura. Facendo combaciare i lati tra loro si ottengono tre triangoli che chiamiamo triangoli piegati una volta. Il miracolo, scoperto da così poco tempo, si mostra subito: i tre triangoli piegati una volta sono congruenti tra loro. Ripeto, non sono solo equivalenti, ma sono proprio congruenti! Pitagora si starà mordendo le mani...

Il gioco, però, può continuare.

Prendiamo il triangolo piegato una volta che presenta le sue tre mediane, come mostra la Fig. 3, a sinistra.

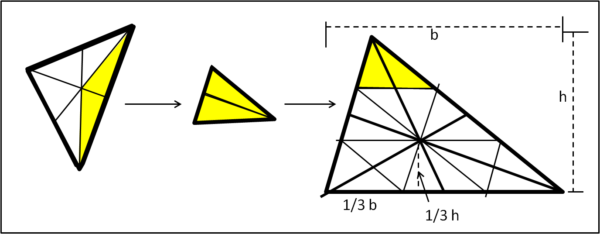
Possiamo, perciò, eseguire nuovamente la rotazione dei due triangoli gialli, come fatto per il triangolo di partenza e ottenere un triangolo giallo che chiamiamo triangolo piegato due volte. La stessa cosa va fatta per gli altri quattro triangoli, che, ovviamente, permettono di costruire tre triangoli congruenti tra loro. Il triangolo piegato due volte  risulta essere simile al triangolo di partenza e si può facilmente provare tenendo conto delle parti di mediane utilizzate. Non solo, però... esso ha un'area che è nove volte più piccola. Non è certo difficile tracciare alcune rette parallele e disegnare i nove triangoli tra loro congruenti (parte destra della figura). Essa permette di dimostrare la congruenza dei tre triangoli piegati una volta.

Esercizio: Indicando adeguatamente i vari angoli che contiene il triangolo così disegnato è facile dimostrare che i triangoli piegati una volta sola hanno tutti gli angoli uguali. Avendo, ovviamente la stessa area, devono essere congruenti tra loro.

Con questi punti di partenza si possono eseguire ulteriori costruzioni. Magari, qualcuna ancora sconosciuta... Provate!

SOLUZIONE dell'ESERCIZIO.

Il nostro bravissimo sprmnt21 ha risolto l'esercizio in modo rapido ed elegante che vorrei riassumere di seguito (ho usato il terzo criterio di uguaglianza, ossia due triangoli sono congruenti se hanno i tre lati congruenti).

Fondamentale è la rotazione di 180° dei triangoli AOM3  e COM2 attorno a M3 e M2, rispettivamente.  Si ottiene la Fig. 4.

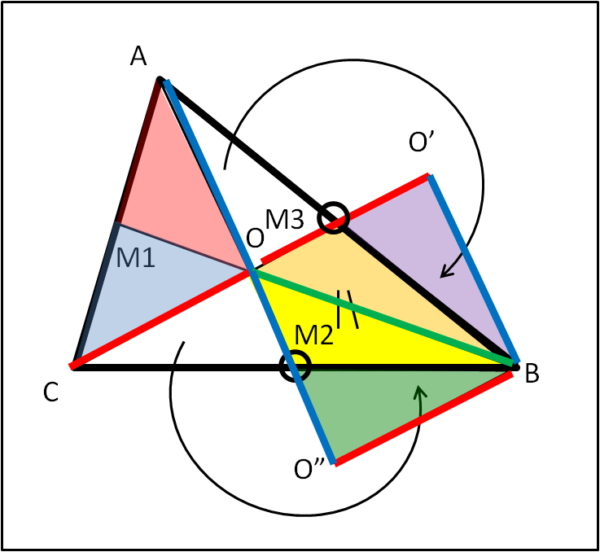
Nella figura a lati uguali è stato dato lo stesso colore (rosso, blu e verde). Sfruttando la proprietà del baricentro che divide le mediane in due parti, una doppia dell'altra, possiamo scrivere:

OO’ = 2 OM3 = CO = O”B

OO” = 2OM2 = AO = O’B

OB in comune.

Ne segue immediatamente che i triangoli  OBO" e OBO' sono congruenti.

La rotazione suggerita da sprmnt21 è veramente "geniale", molto meglio di quella "ufficiale". Ancora un bravo a lui!