Chi non conosce la formula che segue

e^iπ + 1 = 0

E' la celebre identità di Eulero, considerata da molti la più bella formula della matematica, dato che lega tra di loro i suoi principali attori: e, i, π, 1, 0.

Ma Eulero non si è certo limitato a questa relazione.  Egli è considerato il re della matematica, superando anche Gauss e lo stesso Archimede.  A questo riguardo devo fare un "mea culpa" riguardo alla descrizione matematica dei solidi a n dimensioni. Vale la pena ricordare il lungo articolo scritto a riguardo (QUI , magari rileggetelo...) dove abbiamo usato, in modo un po' empirico una formula che si deve, fondamentalmente, al grande Eulero.

Iniziamo da lontano e vediamo di arrivare al dunque, scusandoci con Eulero per averlo un po' trascurato...

Consideriamo la semplice relazione:

(x + 2)³

Non è certo difficile eseguire il cubo e ottenere:

(x + 2)³ = 1 x³ + 6 x² + 12 x¹ + 8 x^o

I coefficienti in grassetto ci dicono qualcosa? No? Pensiamoci bene e consideriamo un cubo...

Quanti vertici ha un cubo? Facile, 8.

Quanti spigoli ha? Ancora facile, 12

Quante facce ha? Sempre facile, 6

Quanti solidi completi otteniamo (quanti volumi)? beh.. 1, proprio il cubo.

Possiamo concludere che i coefficienti del cubo del binomio rappresentano proprio le caratteristiche principali del nostro solido: vertici, spigoli e facce.

Una combinazione... direi proprio di no. Proviamo a verificare se la faccenda si ripete anche per una diversa dimensione. Ad esempio, portiamoci a due. Il cubo diventa un quadrato... Esso ha quattro vertici e quattro spigoli; inoltre la figura completa (il quadrato, ossia faccia) è ovviamente una...

(x + 2)² = 1 x² + 4x¹ + 4 x⁰

Perfetto! Funziona...

e se passassimo a una sola dimensione? Avremmo due vertici e una figura totale (proprio il segmento).

(x + 2)¹ = 1 x + 2x⁰

Tutto ci spinge a credere che l'esponente possa essere qualsiasi, anche maggiore di 3. Per n = 4, avremmo:

(x + 2)⁴ = 1 x⁴ + 8 x³ + 24 x² + 32 ^x + 16 x⁰

Ebbene sì, questa formula ci regala il numero di vertici (16), di spigoli (32), di facce (24). di "volumi" (8) e di ipervolumi (1). In altre parole descrive perfettamente l'ipercubo o tesseratto. Uno dei modi più utilizzati per cercare di rappresentarlo nelle tre dimensioni è quello della Fig. 1 ...

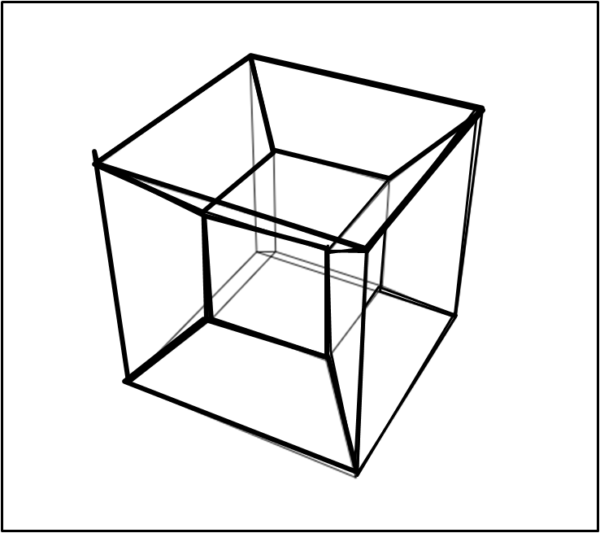
Bene, la formula precedente ci conferma che questa rappresentazione è veramente azzeccata. Contiamo i vertici, gli spigoli, le facce, i volumi e otteniamo proprio 16, 32, 24, 8. I "volumi" sono le parti di spazio a tre dimensioni compresi tra le facce. Ovviamente, alla fine, otteniamo 1 ipercubo.

La Fig. 2 aiuta nel distinguere le varie parti.

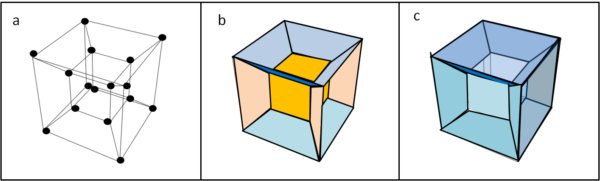
In (a) abbiamo i vertici (16). La stessa figura ci permette di calcolare gli spigoli (32). La (b) individua le facce: 8 azzurre, 4 rosa, 6 arancioni (cubo interno) e 6 del cubo esterno. Totale 24. Infine, la (c) individua i "volumi": 6 volumi azzurri a sezione trapezoidale, 1 cubo interno, 1 cubo esterno, ossia 8 volumi.

Vale la pena ricordare che questi coefficienti così importanti per descrivere matematicamente dei solidi in n dimensioni sono definiti da un celebre triangolo numerico, quello di Tartaglia o di Pascal.

Torniamo al nostro binomio

(x + 2)ⁿ

e sviluppiamolo nuovamente, in successione, per vari valori di n

(x + 2)⁰ = 1x⁰

(x + 2)¹ = 1x¹ + 2x⁰

(x + 2)² = 1x² + 4 x¹ + 4x⁰

(x + 2)³ = 1x³ + 6x² + 12 x¹ + 8 x⁰

(x + 2)⁴ = 1x⁴ +   8x³ +  24 x²  + 32 x¹  + 16x⁰

Ovviamente, siamo liberi di dare a x i valori che preferiamo. Scegliamo x = - 1

Otteniamo:

(-1 + 2)⁰ = 1

(-1 + 2)¹ = 1(-1) + 2

(-1 + 2)² = 1(-1)² + 4 (-1) + 4

(-1 + 2)³ = 1(-1)³ + 6(-1)² + 12 (-1) ¹ + 8

(-1 + 2)⁴ = 1(-1)⁴ +   8(-1)³ +  24 (-1)²  + 32 (-1)¹  + 16

ossia:

1 = 1

1 = - 1 + 2

1 = 1  - 4 + 4

1 = - 1 + 6 - 12  + 8

1 = 1 - 8 +  24   - 32   + 16

Portiamo 1 e - 1 di destra nella parte sinistra, ottenendo

0  = 0

2  =  2

0   =  - 4 + 4

2  = 6  -12 + 8

0 = -8 + 24 - 32 + 16

Ricordiamoci cosa significano i coefficienti di destra e indichiamoli come V = vertici, S = spigoli, F = facce, C = volumi (nelle tre dimensioni)

0 = 0

2 = V

0 = - S + V = V - S

2 = F - S + V = V - S + F

0 = - C + F - S + V = V - S + F  - C

Soffermiamoci sulla terza, quella che si riferisce a tre dimensioni. Essa dice chiaramente che: il numero dei vertici meno il numero degli spigoli più il numero delle facce è uguale a 2. Questo vale per qualsiasi poliedro convesso a tre dimensioni ed è proprio la bellissima formula di Eulero. Ricordiamo che per poliedro convesso si intende qualsiasi poliedro tale cha il segmento che unisce  due qualsiasi punti interni al poliedro sia sempre INTERNO al poliedro.

Questa formula permette di calcolare le facce o i vertici o gli spigoli di qualsiasi poliedro convesso conoscendo i vertici e gli spigoli e via dicendo.

La formula di Eulero è stata generalizzata alle n dimensioni, tenendo presente i valori 2 e 0 che sono stati ottenuti nella tabella precedente, da Ludwig Schlaefli (1814 -1895).

La matematica non ha paura delle n dimensioni!