Un articolo che riduce di molto l'importanza della spirale aurea. Non picchiatemi, però ... sono dispiaciuto anch'io.

Una delle grandi domande che l'uomo si è posto da secoli e secoli può essere riassunta così: la matematica è una creazione dell'uomo per descrivere la Natura o è la Natura stessa che segue leggi matematiche? La sequenza di Fibonacci e la spirale aurea che ne consegue sembrerebbero fornire una risposta inequivocabile. La Natura segue una legge matematica e basta guardarsi attorno per convincersi. Le galassie, i cicloni, i fiori, le conchiglie dei molluschi e molto altro ancora sembrano seguire perfettamente una ben determinata serie numerica, quella che descrive la celeberrima spirale aurea.

Ma è proprio così? Sembra di no... Studi recenti hanno mostrato che la spirale aurea non approssima assolutamente le spirali che appaiono in Natura.

Al limite, possiamo dire che le approssima più o meno. Ne segue che la matematica rigorosa non farebbe altro che descrivere in modo approssimato la Natura. L'illusione che esista qualcosa di magico nella spirale aurea, insito nella costruzione stessa dell'Universo, si scioglie come neve al Sole. La Natura segue le proprie leggi adeguandole alle condizioni al contorno. Ne derivano strutture che sembrano ripetersi in modo matematico. Il fatto è che queste strutture si adeguano alle condizioni in cui "vivono", cercando di minimizzare l'energia e seguire molti altri requisiti necessari allo scopo.

Nascono così configurazioni che, in qualche modo, si assomigliano. Il passo successivo, ossia quello di cercare di inserirle tutte in un unico processo di armonia e perfezione è del tutto immaginario. La sezione aurea porta all'armonia, ma, in realtà, é ciò che la Natura offre che crea la nostra visione dell'armonia. La spirale aurea non è la causa, ma  riassume in modo approssimativo l'effetto delle complesse azioni della Natura. Approssimandola otteniamo ciò che idealizziamo come perfezione.

Queste conclusioni distruggono, purtroppo, la speranza di trovare una legge universale. La Natura non porta a risultati che sembrano essere descrivibili ESATTAMENTE con un'unica legge matematica.

In realtà, matematicamente parlando, la spirale aurea è una delle infinite spirali (infinite) che si possono creare con numeri reali irrazionali.  Si assomigliano tutte e favorire quella basata sul celebre rapporto irrazionale φ è una nostra creazione e illusione. Forse dovuta alla semplicità della sua costruzione, legata, oltretutto, alla celebre serie di Fibonacci. Pensiamo un attimo a come si costruisce una spirale... in pratica, si devono sovrapporre un moto traslatorio e uno rotatorio. Due moti che dominano gli oggetti della Natura e, quindi, non è difficile pensare che la spirale sia un effetto abbastanza comune.

La visione di un Universo costruito in un certo modo fin dall'inizio sembrerebbe proprio priva di senso e spingerebbe a pensare che il Cosmo e le sue leggi siano un continuo divenire. La meccanica quantistica dovrebbe convincerci che le regole del gioco sono proprio queste e la stessa evoluzione darwiniana ce lo dimostra: l'evoluzione non dipende da un codice originario immutabile, ma dall'adattamento alle condizioni ambientali. Se esse variano, varia anche l'evoluzione. Niente è scritto fin dall'inizio e la probabilità gioca un ruolo determinante. Senza l'asteroide dello Yucatan l'uomo non sarebbe, forse, mai esistito.

Dopo questa premessa anti deterministica e sicuramente poco gradita (io stesso sono rimasto molto deluso dalla limitatezza della spirale aurea), vediamo come  le spirali intese come costruzioni matematiche e non come leggi naturali possano essere estremamente utili per decidere se un numero è razionale oppure no. Un risultato  che delude un po', ma che permette comunque di migliorare le nostre capacità matematiche e, quindi, di cercare di descrivere la Natura sempre meglio, anche se con un linguaggio costruito da noi stessi.

Prendiamo un numero irrazionale, ad esempio √2 o √3, e costruiamo la "loro spirale", seguendo la costruzione usata per quella legata alla sequenza di Fibonacci. Ricordiamo che le radici quadrate sono tutte facilmente costruibili geometricamente, seguendo la spirale (ancora una spirale!) di Teodoro (QUI)

Cominciamo con √2 ...

Sappiamo molto bene come costruire geometricamente un rettangolo in cui il rapporto dei lati sia proprio √2 (così come nel rettangolo aureo il rapporto è uguale a φ = 1.618033...). Prendendo un quadrato di lato 1, la sua diagonale vale √2. Per cui è banale disegnare un rettangolo di lati b = 1 e a = √2. Fissiamo il primo quadrato di lato b e occupiamoci di quello che resta, come mostra la Fig. 1.

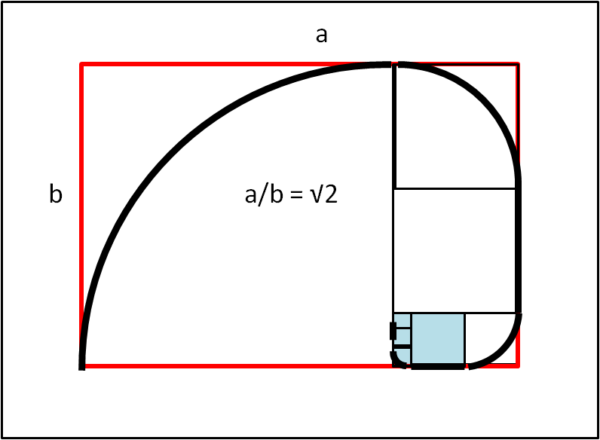
Il rettangolo che resta può essere diviso in due quadrati di lato  a - b e un rettangolo in basso. Quest'ultimo è diviso ulteriormente in due quadrati e in nuovo rettangolo, su cui si può ripetere l'operazione e via dicendo ...

La costruzione si può ripetere all'infinito. Questo fatto comporta che √2 è un numero irrazionale. La dimostrazione è abbastanza banale. Soffermiamoci sul rettangolo colorato in azzurro. Se esso fosse simile a quello di partenza, ossia con i lati nel rapporto √2, potremmo concludere che la situazione si ripete all'infinito. Calcoliamo quanto valgono i lati di questo rettangolo, facendoci aiutare dalla Fig. 2.

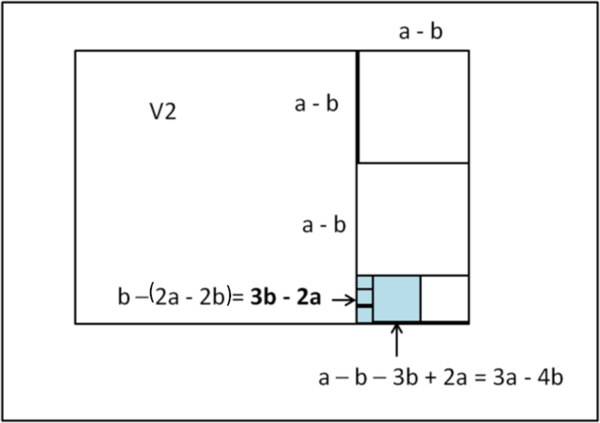
Il lato lungo del rettangolo azzurro vale 3a - 4b, mentre quello corto vale 3b - 2a. Facciamone il rapporto:

(3a - 4b)/(3b - 2a)

dividiamo numeratore e denominatore per b

(3a/b - 4)/(3 -2a/b)

ma a/b = √2

(3√2 - 4)(3 - 2√2)

moltiplichiamo numeratore e denominatore per (3 + 2√2)

(3√2 - 4)(3 + 2√2)/((3 - 2√2)(3 + 2√2)) = (9√2 + 12 - 12 - 8√2)/(9 - 8 ) = √2

Abbiamo ottenuto  proprio √2 come rapporto tra i lati. Siamo, perciò, sicuri che la situazione continuerà a ripetersi fino all'infinito. Questo fatto, tuttavia, indica chiaramente che il tale rapporto DEVE essere irrazionale. Ragioniamo per assurdo, ipotizzando che il rapporto √2 sia razionale, ossia sia uguale al rapporto tra due numeri interi. Ne segue che a e b sono interi e tali sono anche tutte le loro moltiplicazioni o somme con altri numeri interi. Facendo diminuire le dimensioni del rettangolo azzurro troveremo, prima o poi, il caso in cui i lati saranno minori di 1. Ma questo risultato non può essere accettato, dato che sappiamo che devono essere interi. Dobbiamo, quindi, concludere che l'ipotesi di partenza è sbagliata, ossia che a e b non possono essere interi e che, di conseguenza, la radice di due è un numero irrazionale.

La stessa cosa si otterrebbe con √3, dato che la ripetizione su scala minore del rettangolo di partenza implicherebbe nuovamente lati pari a numeri interi e questo , essendo la serie infinita, verrebbe presto contraddetto. Provate a fare i calcoli...

Non è difficile, in conclusione, dimostrare che tutte le radici quadrate (che non siano, ovviamente, quadrati perfetti) sono numeri irrazionali!

Cosa succerebbe, invece, se partissimo da un rettangolo composto da lati pari a numeri interi. Non otterremo certamente una spirale infinita: essa si bloccherebbe a un certo punto, non dando più spazio a rettangoli successivi. Proviamo subito con il rettangolo di lati 10 e 6 (Fig. 3).

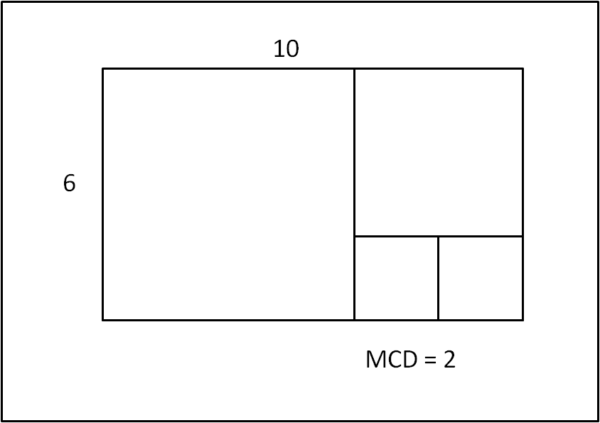
Al quarto quadrato non rimane più spazio per proseguire e il lato di quest'ultimo non è altri che il Massimo Comun Divisore di 6 e 10.

Forse dovremmo convincerci che la matematica è uno splendido linguaggio creato dall'uomo per descrivere le leggi probabilistiche della Natura e smettere di cercare in esse una essenza matematica di partenza... Ma sarà poi la verità?