Il nostro super-matematico sprmnt21 ha dato una soluzione, ma ritengo opportuno pubblicare la mia e lascio a voi la scelta della migliore. Probabilmente ve ne sono anche di più rapide, dato che gli angoli in ballo sono molteplici e qualche passaggio potrebbe essere abbreviato.

SOLUZIONE

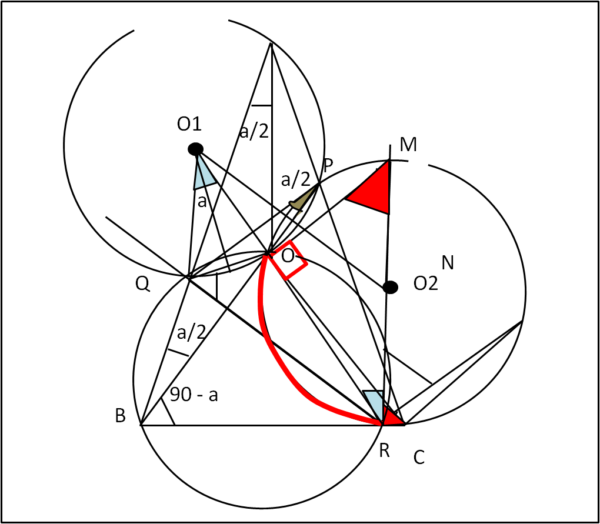
Riportiamo subito una figura che riporti la costruzione da seguire (Fig. 1)

 

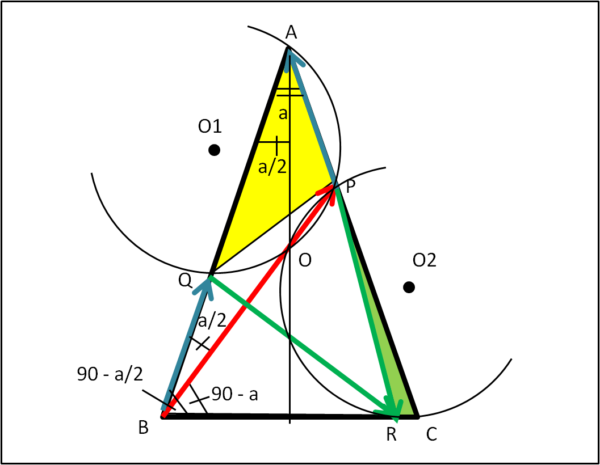
Abbiamo evidenziato alcuni angoli che derivano immediatamente dall'inclinazione data a BP e al valore dell'angolo a. In giallo e in verde i triangoli di cui si individua il circocentro.

Dai dati di partenza si ottiene subito il valore dell’angolo ABP:

ABC = 90 – a/2

ABP = 90 – a/2 – 90 + a = a/2

Ne segue che il triangolo AOB è isoscele, da cui

OB = OA

Attenzione! Anche se sembra ovvio, non sappiamo ancora se O appartenga alla circonferenza di centro O1 e a quella di centro O2 … dobbiamo verificarlo!

Ci sono sicuramente vari metodi, ma noi ci affidiamo ai quadrilateri ciclici.

Consideriamo i triangoli AOP e QOP (colorati in azzurro) di Fig. 2.

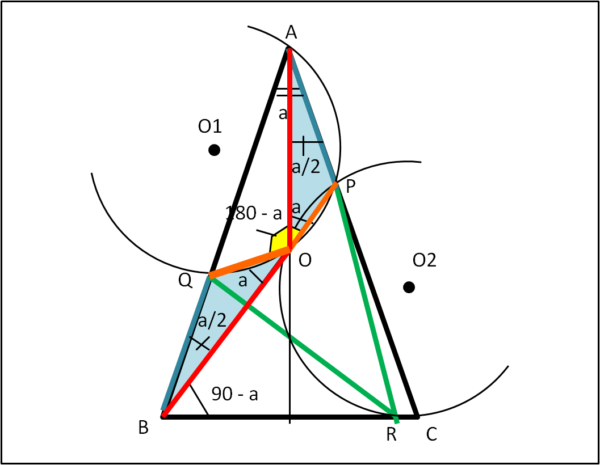
Essi sono congruenti in quanto

AP = QB per le ipotesi di partenza

AO = OB perché lati di un triangolo isoscele

OAP = OBQ = a/2

Ne segue che QO = OP

Ricaviamo inoltre che:

AOP = QOB = a/2 + a/2 = a

Ne segue che  QOP = 180 – a

QAP + QOP = a + 180 – a = 180

Il quadrilatero  AQOP è ciclico, per cui O deve stare sul cerchio circoscritto ad AQP (di centro O1).

Guardiamo la Fig. 3

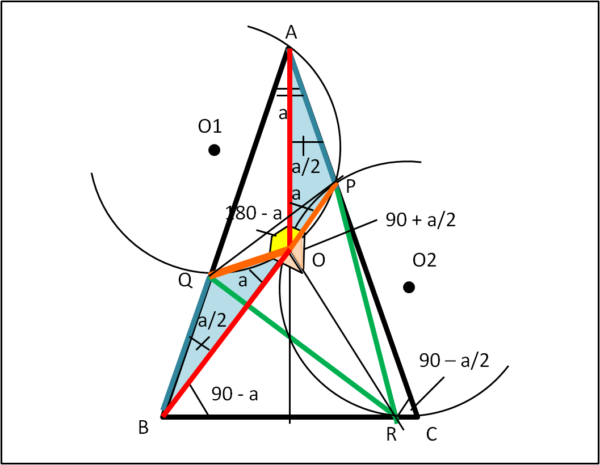
QPR triangolo isoscele. Dato che QO = OP, RO biseca l’angolo QRP.

ROP = ROQ = QOP/2

QOP = 180 + a

ROP = 90 + a/2

PCR + ROP = (90 - a/2) + (90 + a/2) = 180

PCRO  ciclico

O deve appartenere sia al cerchio di centro O2 sia al cerchio di centro O1 (così come P).

Tracciamo la congiungente  O1O2 (Fig. 4). O1P = O1O  e O2P = O2O, il che vuol dire che P e O sono equidistanti  sia da O1 che da O2. Ciò comporta che PO, ossia PB,  è perpendicolare a O1O2.

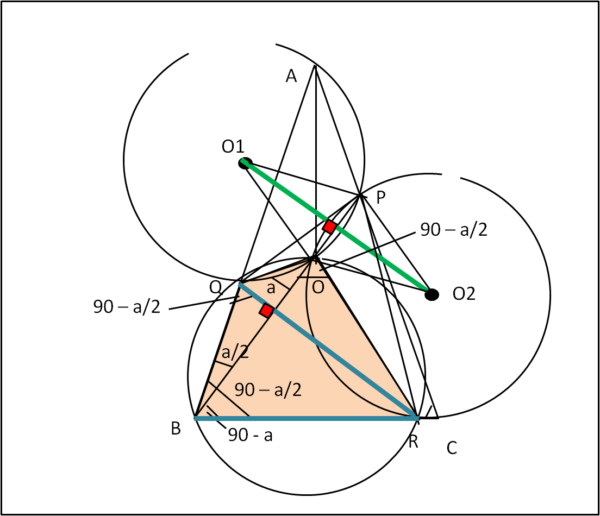
Il quadrilatero  QORB è ciclico. Infatti:

QOR = 90 + a/2

QBR = 90 – a/2

QOR + QBR = 180°

Sappiamo, inoltre, che

QOR = POR = 90 + a/2

BQR = BOR   (angoli alla circonferenza)

BOR = 90 + a/2 – a = 90 – a/2

BQR = 90 – a/2

Ma risulta anche che:

QBC = 90 – a/2

Il triangolo BQR è isoscele

Ne segue che:

BR = QR

A questo punto possiamo cambiare la nostra tesi e scriverla come:

O1O2 = QR

E' immediato dire che O1O2 è parallelo a QR, dato che QR è perpendicolare a  BP.

Ne segue che se anche QO1 fosse parallelo a O2R dimostreremmo la tesi, dato che O1QRO2 sarebbe un parallelogramma.

Concludiamo disegnando la Fig. 5, dove MR è un diametro del cerchio di centro O2.

MOR = 90

OMR  = OCR  (angoli alla circonferenza)

OCR = 90 - a

O2RO = 90 – 90 + a  = a

D'altra parte, sappiamo che:

QO1O = 2 QAO (angolo al centro doppio di quello alla circonferenza)

QO1O = 2 a/2 = a

La trasversale O1R forma due angoli uguali con O1Q e O2R

Essi sono, perciò, paralleli

CVD