Soluzione (una delle tante possibili) al problema del numero primo ****
Andiamo avanti con calma, spiegando tutti i passaggi...
Innanzitutto, scriviamo in altro modo la nostra ipotesi, ossia:
(ac + bd) = (a + b + d - c)(b + c + d - a)
ac + bd = ab + ac +ad – a2 + b2 + bc + bd –ab + db + dc + d2 – ad – cb – c2 –cd + ac
0 = + ac – a2 + b2 + bd + d2– c2
(a2 + c2 – ac) = ( b2 + d2 + bd) .... (1)
Questa uguaglianza è fondamentale per disegnare un quadrilatero sicuramente ciclico.
Consideriamo, in Fig. 1, il triangolo XYW tale che XW= a, XY = c e YW = √(a2 + c2 – ac)
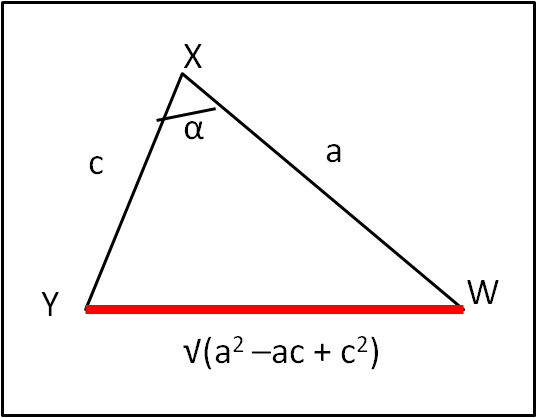
Il lato maggiore di questo ipotetico triangolo è a, infatti:
a2 > √(a2 + c2 – ac) = √(a2 + c (c –a)) ,
ma c – a minore di zero per cui vale la disuguaglianza
Abbiamo detto "ipotetico" triangolo, Infatti, non è detto che tre segmenti qualsiasi formino un triangolo. Per esserne sicuri basta provare che la somma dei lati minori sia maggiore del lato maggiore.
Attenzione: se dimenticassimo questo passaggio, la soluzione non sarebbe corretta!
c + √(a2 + c2 – ac) > a ?
√(a2 + c2 – ac) > a – c
a2 + c2 – ac > a2 + c2 – 2ac
-ac > -2ac
ac < 2ac
verificata! Il triangolo esiste.
Applichiamo il teorema del coseno a questo triangolo, indicando l’angolo in X come alfa. Ricordiamo... il quadrato di un lato è uguale alla somma dei quadrati degli altri due lati meno due volte il prodotto di questi due lati per il coseno dell'angolo opposto al lato di partenza. Nel nostro caso:
(a2 + c2 – ac)= a2 + c2 – 2ac cos(α) .... (2)
0 = ac (1 - 2cos(α))
2cos(α) - 1 = 0 dato che ac non può essere zero, poiché a > c > 0..
cos(α) = 1/2
Penso che non vi sia bisogno di calcolatrice per sapere che l'angolo il cui coseno è 1/2 vale 60°. Questa è una nozione che è considerata ben nota in questo tipo di competizione.
α = 60°
Costruiamo, adesso, un triangolo che abbia nuovamente YW come lato, ma questa volta come lato maggiore. Sia YWZ questo triangolo, con ZW = d e YZ = b. Questo triangolo esiste sicuramente dato che
b + d > √(a2 + c2 – ac) ?
può essere scritta (per merito della (1)), come:
b + d > √(b2 + d2 + bd)
b2 + d2 + 2bd > b2 + d2 + bd
verificata!
Applichiamo il teorema del coseno a quest’ultimo triangolo chiamando β l’angolo in Z (Fig. 2).
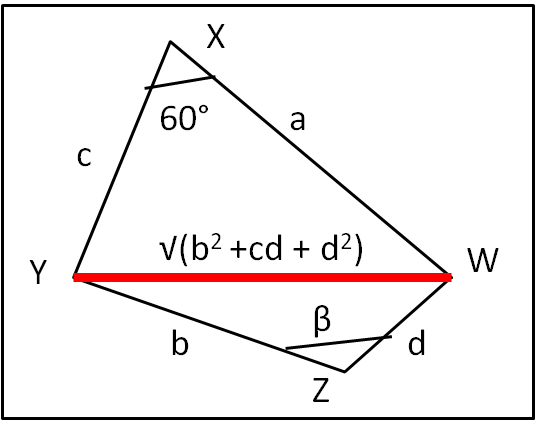
b2 + d2 + bd = b2 + d2 – 2 bd cos(β) .... (3)
bd = - 2 bd cos(β)
bd(1 + 2cos(β)) = 0
1 + 2cos (β) = 0
cos(β)= -1/2
β = 120°
Abbiamo dimostrato che α + β = 180°, ossia che il quadrilatero YXWZ è ciclico.
Non ci rimane che applicare il teorema di Tolomeo, nella sua versione più “forte".
WY2 = (ab + cd)(ad + bc)/(bd + ac) .... (4)
Questa versione del teorema è solitamente data come conosciuta. Noi non l'abbiamo mai richiamata e vale, perciò, la pena di ricavarla con semplici passaggi, sfruttando il fatto che:
β= 180 - α
ossia:
cos (β) = - cos(α)
Possiamo scrivere:
a2 + c2 – 2ac cos(α) = b2 + d2 + 2 bd cos(α)
2 cos(α)(ac + bd) = (a2 + c2 – b2 – d2)
2 cos(α) = (a2 + c2 – b2 – d2)/(bd + ac)
Ricordando la (2)
WY2 = a2 + c2 – ac (2 cos(α))
si ha, sostituendo...
WY2 = a2 + c2 – ac (a2 + c2 – b2 – d2)/(bd + ac)
WY2 = ( (a2 + c2)(bd + ac) – ac (a2 + c2 – b2 – d2))/(bd + ac)
WY2 = (a2bd + a3c +c2bd +c3a – a3c –ac3 + acb2 + acd2)/(bd + ac)
WY2 = (a2bd +c2bd + acb2 + acd2)/(bd + ac)
WY2 = (ab (ad +cb)+ cd(bc+ ad))/(bd + ac)
WY2 = (ab + cd)(ad + bc)/(bd + ac)
c.v.d.
Non ci resta, adesso, che ragionare sul valore di WY2
Possiamo scriverlo, come ben sappiamo:
WY2 = b2 + d2 + bd
Ma questa scrittura ci dice che WY2 deve essere intero
Infatti: b intero, d intero e tale deve essere anche bd. Ne segue che b2 è intero così come d2. La somma di interi è sempre un numero intero.
Più in generale, dobbiamo ricordare che la somma, la differenza e il prodotto di numeri interi deve sempre essere un numero intero (non il rapporto, però!).
Ciò che ci importa, comunque, è che l'espressione
(ab + cd)(ad + bc)/(bd + ac) .... (5)
(uguale a WY2) sia un numero intero.
Sappiamo però che
(ab + cd) > (bd + ac) > (ad + bc) .... (6)
Come mai ne siamo sicuri?
a > d
da cui
a(b – c) > d(b – c)
ab – ac > bd – cd
ab + cd > ac + bd
e
c > d
da cui
c(a – b) > d (a – b)
ac + bd > ad + bc
Indichiamo
ab + cd = p
bd + ac = x
ad + bc = y
e, quindi:
p > x > y
La (6) ci dice che:
p (y/x) intero
Noi sappiamo, però, che y/x deve essere minore di 1 dato che x > y
Ipotizziamo che p sia primo...
Un numero primo moltiplicato per un numero minore di 1 dà come risultato un intero se e solo se
x = p oppure x = 1
ma questo è impossibile in quanto sappiamo che p > x e x >1. Ne segue che
p NON può essere primo!






7 commenti
La dimostrazione geometrica (molto interessante ma alquanto complessa a dire il vero) si sposa perfettamente con la dimostrazione prettamente algebrica.
Difatti, partendo dalla considerazione di una delle (infinite) terne pitagoriche ottenibili con il procedimento descritto nel mio commento relativo al quiz (nell'esempio che segue la terna viene generata secondo un m=4 e un n dispari ≥ 9), generalizzando, si può scrivere:
sistema in 4 equazioni che ammette solo soluzioni intere se k è un qualunque intero dispari ≥ 9 (per k dispari minore di 9 il sistema ammette soluzioni intere che lo risolvono, ma non viene rispettato il vincolo di a>b>c>d>0)
e scartando eventuali soluzioni negative, si ottiene:
e sostituendo k con un qualsiasi valore dispari maggiore o uguale a 9, verifica senza ombra di dubbio la
condizione iniziale di a>b>c>d>0.
Allora:&space;\cdot&space;k^2+(k^2-4K-16)&space;\cdot&space;16)
e sviluppando il secondo membro dell'identità, equivale a:
il polinomio secondo k si scompone in:
I due moltiplicatori tra parentesi sono due numeri interi il cui prodotto è uguale ad ab + cd che quindi non può che essere un numero composto.
Quindi mantenendo, come nell'esempio specifico, d fisso uguale a 16 e k variabile (maggiore di 9) si otterranno infiniti quadrilateri con la caratteristica richiesta;
e certamente esisteranno altre coppie m ed n generatrici di terne pitagoriche (una già riportata nel commento al quiz) che conducano alla costruzione del sistema con d fisso e k variabile le cui soluzioni faranno si che
ab + cd è uguale al prodotto di due numeri interi e quindi non può essere primo.
In buona sostanza , la dimostrazione geometrica utilizza un sottoinsieme di quadrilateri con la caratteristica di essere ciclici, con lati di misura intera e che presentano due angoli opposti esattamente pari a 60° e 120°, dell'insieme infinito di quadrilateri possibili,
così come la dimostrazione algebrica utilizza un sottoinsieme di quadrilateri di derivazione "pitagorica" con lati di misura intera, dell'insieme infinito dei quadrilateri possibili.
Per concludere, un immagine del quadrilatero di derivazione pitagorica (quello dell'esempio nel commento al quiz):
Il raggio l'ho calcolato con la formula di Parameshvara (che è applicabile esclusivamente ai quadrilateri ciclici) che equivale a dire che se esiste una circonferenza circoscritta ad un quadrilatero, questo è senz'altro ciclico.
Per curiosità, misurando gli angoli ∠ac e ∠bd, questi risultano di 60° e 120°.
grazie Andy !
caro Andy,
volevo aggiungere che la soluzione geometrica non si sembra particolarmente complessa... In fondo, bisogna solo dimostrare che un certo quadrilatero (di lati proprio a, b, c e d) sia ciclico. Fatto questo, è possibile legare i valori a,b,c e d a un numero intero (versione forte del teorema) e la relazione porta immediatamente alla tesi...
In effetti anche a me pare che la geometria non era invitata a questa festa. Sul frontone dell'ingresso c'era scritto non entri qui chi sia geometra. (Ma ci si può sempre intrufolare.)
Provo a provare la relazione magica (e magistralmente usata allo scopo del quesito) trovata da Vincenzo per altra via.
la relazione da provare è la seguente (oppure l'equivalente con (b^2+d^2+bd)):
(ac + bd) (a^2 + c^2 - ac) = (ab + cd) (bc + ad).
Seguono i passaggi (tutti giustificati, credo, da quanto scritto da Vincenzo)
(ac + bd) (a^2 + c^2 - ac) =
ac (b^2 + d^2 +bd) + bd (a^2+c^2 -ac) =
ab^2c + acd^2 + abcd + a^2bd + bc^2d – abcd =
ab (bc + ad) + cd(ad + bc) =
(ad + bc) (ab + cd)
A mio modestissimo avviso, le “reciproche interazioni” tra la dimostrazione geometrica e quella algebrica raggiungono un equilibrio stabile.
Una piccola notazione:
dove si scrive (a2 + c2 – ac) = ( b2 + d2 + cd) che dimostrerà la ciclicità del quadrilatero generico, sarebbe da correggere; difatti riportando lo sviluppo di
(ac + bd) = (a + b + d - c)(b + c + d - a)
ac + bd = ab + ac +ad –a2 +b2 +bc +bd –ab + db +dc +d2 –ad –cb –c2 –cd +ac
0 = –a2 +b2 +bd +d2 –c2 +ac
(a2 + c2 – ac) = (b2 + d2 + bd)
dove in blu ho evidenziato i termini di egual valore e segno ma collocati in membri opposti,
in rosso i termini di egual valore e segno opposto collocati nello stesso membro.
Nella dimostrazione algebrica, considerando come differenza di quadrati il prodotto
(a + b + d - c)(b + c + d - a) = (b + d)^2 – (a – c)^2
e dato che se una differenza di quadrati è uguale ad un terzo quadrato (nel caso in oggetto ac + bd), si rientra nel teorema di Pitagora, sarà quindi possibile strutturare successivamente un sistema del tutto generale, (considerando anche il quarto lato per il quadrilatero), come il seguente:
∀ j ∈ N={1, 2, 3, 4, …, n – 1, n} con k ≥ 2j + 1
che ammette come soluzioni positive:
Ritornando al sistema e sostituendo i valori generali ottenuti per a, b, c, d nella somma di prodotti ab + cd:
poiché j può essere almeno 1 e k almeno 3, il che dimostra il fatto che ab + cd non può essere primo
Come esempi numerici, riporto una tabella con i valori di j (e di conseguenza k) da 1 in avanti:
dove vengono confermate, attraverso i valori numerici (e si potrebbe continuare all’infinito), le varie dimostrazioni date seguendo il procedimento di tipo geometrico.
Per concludere, tutti i quadrilateri ottenuti seguendo questa procedura possiedono un angolo di 60° e l'opposto di 120° e sono quindi ciclici.
Ovviamente, Andy, mi era "scappato " un bc al posto di bd.
Pienamente d'accordo sul resto..
Secondo me il problema voleva far saltare fuori la versione "forte" di Tolomeo. Chi la ricordava, faceva in fretta ad arrivare al dunque...