Fino a pochi anni fa, se si cercava su internet "problema dei tre corpi" venivano proposti siti di carattere essenzialmente fisico, più o meno complicati. Oggi è molto meglio aggiungere l'aggettivo "fisico" altrimenti si è lanciati nel mondo dei libri e dei film, a causa del romanzo cinese con l'omonimo titolo. Mi sono deciso a guardare qualche episodio della lunga serie TV, che mostra la solita trama piuttosto deludente e allungata a dismisura. Il problema di base è, però, estremamente interessante, così come le sue possibili conseguenze.

Riassumendo: un pianeta che vive in un sistema triplo è costretto a descrivere un'orbita caotica, del tutto imprevedibile, tale da dover subire condizioni climatiche del tutto diverse a seconda della posizione del pianeta rispetto alle stelle (Fig. 1). In realtà basterebbe un sistema doppio per arrivare a queste "tragiche" conseguenze.

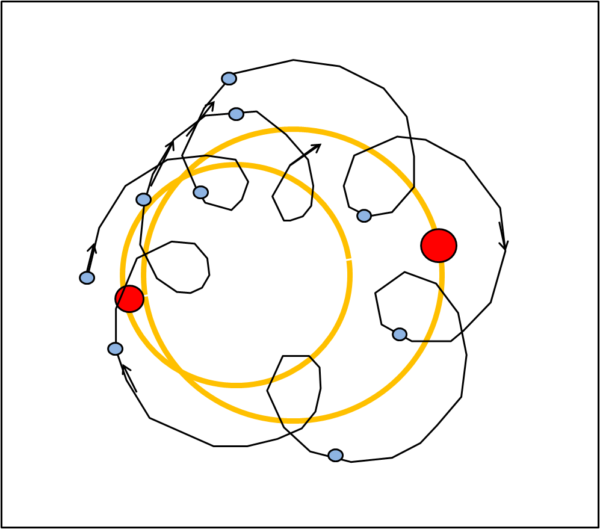
In realtà, qualcosa di simile a quanto descritto nel romanzo l'avevo già anticipato in modo semplice ed ironico in un mio vecchio racconto (Democrazia), dove l'orbita finale era  periodica, ma comportava una netta separazione tra due situazioni orbitali con conseguente ricadute sul comportamento degli abitanti. Vi invito a (ri)leggerlo...

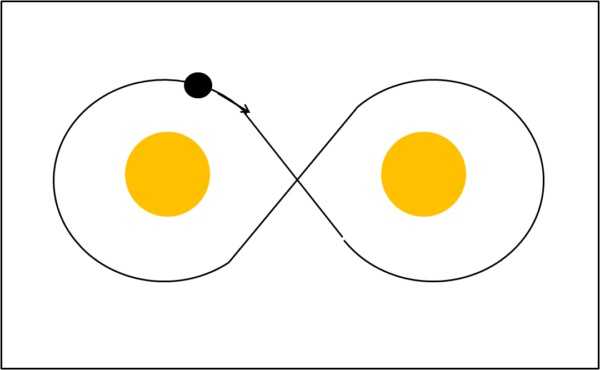
Sul problema dei tre corpi abbiamo già discusso parecchio, ma il romanzo e il successo che sta ottenendo, mi spinge a fare un po' di chiarezza e capire bene quando e perché la sua soluzione analitica sia impossibile. Utilizzerò analogie che , anche se non perfette, aiuteranno (spero) nella comprensione del problema.

Conviene innanzitutto separare il problema dei tre corpi più generale da quello "ristretto".

Quest'ultimo è quello che più importa da un punto di vista pratico, dato che permette di studiare e pianificare le missioni interplanetarie e tenere sotto controllo le orbite degli asteroidi e della stessa Luna attorno alla Terra. In realtà, lo conosciamo molto bene, anche perché Lagrange aveva trovato dei punti  di equilibrio stabili e, quindi, orbite ben descrivibili su tempi scala anche piuttosto lunghi.  il problema dei tre corpi ristretto assume un'ipotesi fondamentale: il terzo corpo ha una massa decisamente più piccola di quella dei due corpi principali. Questa ipotesi si traduce nel fatto che il terzo corpo NON influisce gravitazionalmente sugli altri due. Ne consegue che il baricentro del sistema rimane praticamente fisso e tutto si riduce a valutare istante per istante come giocano le forze gravitazionali dei due corpi principali sull'oggetto di cui si vuole conoscere la traiettoria. Analiticamente non si riesce  fare, ma, in fondo, poco importa dato che possiamo costruire, per via numerica, la traiettoria per piccoli intervalli e ogni volta inserire gli effetti gravitazionali dei due oggetti che seguono nel loro moto la "semplice" legge di Newton.

In realtà, potremmo nuovamente finire nel caos, ma, normalmente, questo avviene  per casi estremamente sfavorevoli. Il problema ristretto è proprio quello che si applica per determinare il moto della Luna (i corpi principali su orbita newtoniana sono il Sole e la Terra) o degli asteroidi ( i corpi principali sono Giove e il Sole). Non è nemmeno difficile aggiungere ulteriori corpi al sistema, tenendo conto di tutti i loro effetti perturbativi: i risultati cambieranno di poco e possono, in qualche modo, essere tenuti sotto controllo variando i tempi di integrazione durante i passaggi più critici.

Ovviamente, per stare tranquilli sull'evoluzione futura, bisogna evitare certe configurazioni "critiche". Mi riferisco, in particolare, alle risonanze e/o ai passaggi ravvicinati. Sappiamo molto bene che il ripetersi periodico di una stessa configurazione di un asteroide con Giove o una eccessiva vicinanza tra il corpo di massa trascurabile e uno dei due oggetti principali, può portare a un'orbita del tutto caotica su tempi relativamente brevi (pochi milioni di anni).

Completamente diverso è, invece, il problema dei tre corpi, quando essi hanno tutti una massa comparabile. Ognuno influenza gravitazionalmente gli altri due e basta una minima incertezza dovuta a una perturbazione tralasciata o proprio all'approssimazione usata da diversi calcolatori per cadere in orbite caotiche del tutto imprevedibili. Prima di proseguire ricordiamo ancora che un'orbita caotica rimane, comunque, sempre qualcosa di deterministico. Il caso non c'entra niente e ciò che capita in un certo tempo t_i dipende completamente dal tempo precedente t_i-1.

Il vero problema è che non siamo in grado di valutare con esattezza estrema le condizioni del sistema. Basta che su uno dei tre corpi sbatta le ali una farfalla per cambiare in modo drastico l'andamento futuro. Potremmo dire che la vera causa di tutto ciò deriva dal fatto che nel problema generale dei tre corpi il baricentro del sistema non è assolutamente stabile, ma varia continuamente. Preferisco, però, proporvi una visione  molto più semplice ma, a mio parere, più intuitiva. Ricordiamo, ancora, che nel caso ristretto l'oggetto che si sta studiano subisce soltanto, mentre, nel caso generale influenza anche.

Sia P una pallina (rossa) posta all'inizio di una certa traiettoria. Essa viene mossa con una certa velocità in modo da descrivere la curva della parte alta di Fig. 2.

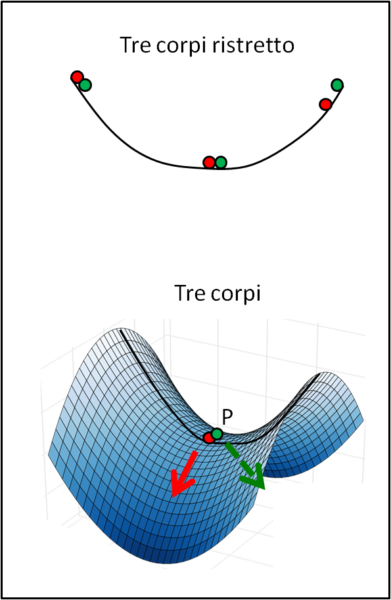
Lanciamo ora un'altra pallina (blu)  cambiando leggermente la sua velocità e/o la posizione iniziale (non troppo però) La posizione finale è molto simile a quella precedente. L'errore iniziale si ripercuote in un errore finale del tutto comparabile, almeno per tempi "umani" di interesse pratico. Le posizioni finali delle due palline non sono esattamente uguali, ma sufficientemente uguali per lo scopo prefissato. La sonda New Horizons arriva su Plutone, un certo asteroide raggiunge il suo istante di opposizione, un certo satellite artificiale resta sotto stretto controllo, la Luna ripete perfettamente le sue fasi, ecc., ecc.

Consideriamo, adesso, la stessa situazione di partenza ma portata in uno spazio tridimensionale (parte bassa di Fig. 2). Il Punto P, in particolare, non è più un punto di equilibrio stabile, ma diventa un punto di "sella", ossia è nello stesso momento sia stabile che instabile. Se la pallina arriva in quel punto con velocità diversa anche in modo infinitesimo (o se preferite assume la stessa velocità in posizioni non esattamente uguali), la pallina può andare sia a destra che a sinistra, ossia cambiare drasticamente la sua traiettoria. Per piccola che sia la differenza riscontrabile, la biforcazione  è sempre possibile: la sua traiettoria  diventa, perciò, caotica.

La serie di immagini della Fig. 3 illustra l'evolversi della situazione.

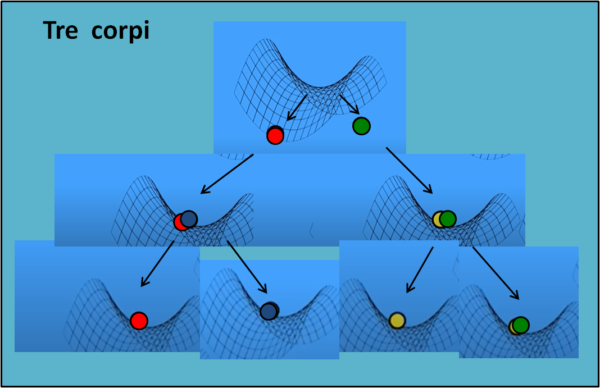
Il grande Poincaré aveva detto chiaramente  che non era possibile trovare una soluzione analitica. Pochi anni dopo, però, Karl Sundman ha ribaltato la situazione... L'utilizzo di serie convergenti estremamente complesse, che utilizzano certi punti "singolari" come  dati fondamentali, è riuscito a prospettare una soluzione analitica. Tuttavia, qual è la sua utilità? Il metodo introduce una serie che  converge in modo estremamente lento: essa ha bisogno, infatti,  di 10^8000000 termini. Qualcosa di impensabile e del tutto inutile per gli scopi pratici.

Immaginiamo, adesso, di lanciare la nostra pallina con una configurazione ben definita. A questo punto introduciamo l'evoluzione attraverso l'integrazione numerica.  In generale le traiettorie continuano a cambiare in un gioco sempre nuovo. Non sempre, però... sono state scoperte situazioni  periodiche, che si ripetono continuamente. Ovviamente, esse sono state trovate con le integrazioni numeriche (e non in modo analitico), ma forniscono un qualcosa che assomiglia di molto alle soluzioni particolari di Lagrange per il problema dei tre corpi. Oggi se ne continuano a trovare, anche molto strane e complicate. Alcune di esse sono riportate nella Fig. 4.

Notiamo, in particolare, la più semplice tra di esse, quella in cui i tre corpi sembrano proprio rincorrersi lungo una traiettoria ad "otto". Non dimentichiamo, però, che queste soluzioni sono state trovate numericamente. Qualsiasi perturbazione non prevista nel modello porterebbe alla loro distruzione. Esse sono prevedibili assumendo co9nfigurazioni particolari invarianti e svolgendo le integrazioni numeriche, ma non ammettono variazioni durante la loro evoluzione.

In un sistema a tre corpi, una delle classiche soluzioni è la formazione di un sistema binario con l'espulsione della terza stella (Fig. 4 a,b).

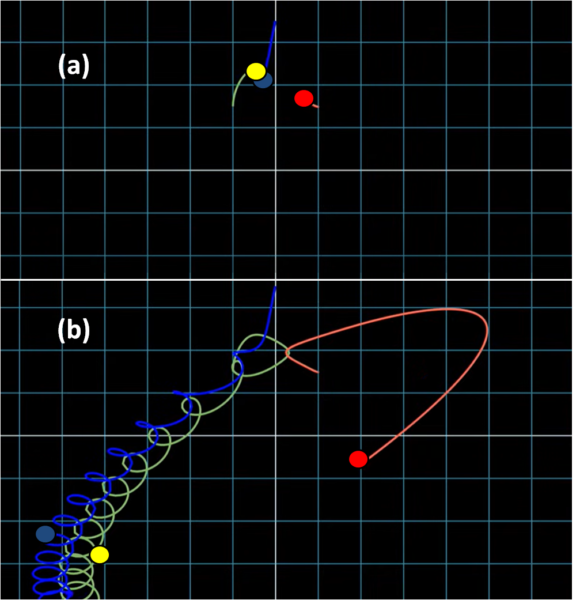
Quest'ultima viene lanciata nello spazio a ipervelocità. Oggi, sappiamo che esistono molte stelle di questo tipo nella nostra stessa galassia. La loro origine potrebbe essere proprio un sistema caotico. Una ghiotta occasione per studiare le conseguenze dinamiche di un sistema a tre corpi.

Concludiamo, tornando al romanzo di partenza. Il pianeta sarebbe in un sistema sicuramente caotico ed esso sarebbe influenzato dalle tre stelle in modo sempre diverso. A volte potrebbe trovarsi troppo vicino a una di esse, a volte potrebbe essere su una traiettoria in grado di farlo fuggire per sempre. Periodi di calma alternati a periodi veramente critici. Non a caso gli altri pianeti di del sistema non esistono più... Quanto potranno ancora sopravvivere i suoi abitanti? Non possono fare previsioni e non gli resta che fuggire verso un pianeta sicuramente (o quasi...) stabile. Anche per i trisolariani il problema rimane irrisolvibile! Possiamo dargli completamente torto? Sicuramente noi tenteremmo di fare lo stesso.